InverseGaussianDistribution
InverseGaussianDistribution[μ,λ]
平均が μ で尺度母数が λ である,逆ガウス(Gauss)分布を表す.
InverseGaussianDistribution[μ,λ,θ]
母数が μ,λ,θ の一般化された逆ガウス分布を表す.
詳細

- InverseGaussianDistribution[μ,λ]は逆正規分布あるいはWald分布としても知られている.
- InverseGaussianDistribution[μ,λ,θ]はSichel分布としても知られている.
- 逆ガウス分布における値
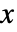 の確率密度は,
の確率密度は,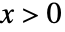 では
では 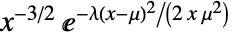 に比例し,
に比例し,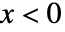 では0である. »
では0である. » - 一般化された逆ガウス分布における値
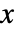 の確率密度は
の確率密度は 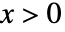 のときは
のときは 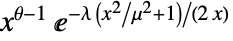 に比例し
に比例し 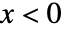 では0である.
では0である. - InverseGaussianDistributionでは,μ および λ は任意の正の実数でよく,θ は任意の実数でよい.
- InverseGaussianDistributionでは,λ と μ は単位次元が等しい任意の数量でよく,θ は無次元量でよい. »
- InverseGaussianDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- InverseGaussianDistribution[μ,λ,θ]は,区間
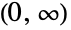 上で定義され,実数 θ(「指数母数」と呼ばれる)と2つの正の実数 μ(分布の平均)と λ (「尺度母数」と呼ばれる)でパラメータ化された連続統計分布を表す.逆ガウス分布の確率密度関数(PDF)は,大体において単一の「峰」(最大値)を持つ単峰性で,全体的な形(高さ,広がり,
上で定義され,実数 θ(「指数母数」と呼ばれる)と2つの正の実数 μ(分布の平均)と λ (「尺度母数」と呼ばれる)でパラメータ化された連続統計分布を表す.逆ガウス分布の確率密度関数(PDF)は,大体において単一の「峰」(最大値)を持つ単峰性で,全体的な形(高さ,広がり,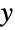 軸周辺での集中度)は μ,λ,θ の値によって決定される.これに加え,PDFの裾部はPDFが
軸周辺での集中度)は μ,λ,θ の値によって決定される.これに加え,PDFの裾部はPDFが 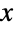 の大きい値について代数的にではなくむしろ指数的に減少するという意味で「薄い」(この動作は分布のSurvivalFunctionを分析することで数量的に正確にすることができる).3引数の形は一般化された逆ガウス分布あるいはSichel分布と呼ばれることがあるのに対し,2母数の形InverseGaussianDistribution[μ,λ](
の大きい値について代数的にではなくむしろ指数的に減少するという意味で「薄い」(この動作は分布のSurvivalFunctionを分析することで数量的に正確にすることができる).3引数の形は一般化された逆ガウス分布あるいはSichel分布と呼ばれることがあるのに対し,2母数の形InverseGaussianDistribution[μ,λ](
これはInverseGaussianDistribution[μ,λ,-1/2]に等しい)は「逆ガウス分布そのもの」あるいはWald分布と呼ばれることがある. - 他のいくつかの確率分布ペアの間にある「逆」の関係 (例:InverseGammaDistributionはGammaDistributionの逆分布でInverseChiSquareDistributionはChiSquareDistributionの逆分布)やある種の確率変数の逆数の動作で特徴付けられるものとは異なり,InverseGaussianDistributionは,正規(ガウス)分布に従う変量XNormalDistribution[μ,σ]の逆数 1/Xが従う分布ではない.InverseGaussianDistribution の「逆」という言葉は,正のドリフトがあるブラウン運動が一定の正のレベルに達するまでの時間が逆ガウス分布に従うのに対し,ガウス分布は固定時間におけるブラウン運動のレベルを説明することによる.InverseGaussianDistributionは,そのブラウン運動における役割に加え,Wiener過程,工学,信頼性理論,職業被曝データ,危険分析,保険統計学の研究におけるツールとして使われている.
- RandomVariateを使って,逆ガウス分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,InverseGaussianDistribution[μ,λ,θ]](より簡略な表記では xInverseGaussianDistribution[μ,λ,θ])を使って,確率変数 x が逆ガウス分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 逆ガウス分布の確率密度関数および累積分布関数は,PDF[InverseGaussianDistribution[μ,λ,θ],x]およびCDF[InverseGaussianDistribution[μ,λ,θ],x]を使って得られる.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合が逆ガウス分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリック逆ガウス分布を推定することが,FindDistributionParametersを使ってデータを逆ガウス分布にフィットすることができる.ProbabilityPlotを使って記号逆ガウス分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号逆ガウス分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された逆ガウス分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って逆ガウス分布を含む高次元分布を構築することが,ProductDistributionを使って逆ガウス分布を含む独立成分分布の結合分布を計算することができる.
- InverseGaussianDistributionは,他の多くの分布と密接な関係がある.例えば,NormalDistributionについてのCumulantGeneratingFunctionがスケールされていないInverseGaussianDistributionのそれの逆関数であるという意味でNormalDistributionと関係している.InverseGaussianDistributionにはGammaDistributionとしてInverseGammaDistributionが,また極限の場合としてのHyperbolicDistributionがある.InverseGaussianDistributionは,WeibullDistribution,LogNormalDistribution,ChiSquareDistribution,InverseChiSquareDistribution.FRatioDistributionとも関係している.
例題
すべて開くすべて閉じる例 (6)
スコープ (10)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (3)
正のドリフトがあるブラウン運動が2に達するまでの時間の分布を求める:
InverseGaussianDistributionをデータにフィットする:
あるデバイスの寿命が逆ガウス分布に従うとする.このデバイスの信頼性を求める:
粒子が媒介物の中を移動する際にその粒子は分散によってエネルギーを失う.エネルギー損失のスペクトルはLindhard and Nielsenの可積分もモデルによるとInverseGaussianDistribution断面を持つという:
特性と関係 (6)
![]() 個のInverseGaussianDistributionに従う独立同分布変数の総和はInverseGaussianDistributionに従う:
個のInverseGaussianDistributionに従う独立同分布変数の総和はInverseGaussianDistributionに従う:
TransformedDistributionを使って総和の分布を求める:
考えられる問題 (2)
InverseGaussianDistributionは,μ が正の実数ではないときは定義されない:
InverseGaussianDistributionは,λ が正の実数ではないときは定義されない:
テキスト
Wolfram Research (2007), InverseGaussianDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/InverseGaussianDistribution.html (2016年に更新).
CMS
Wolfram Language. 2007. "InverseGaussianDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/InverseGaussianDistribution.html.
APA
Wolfram Language. (2007). InverseGaussianDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseGaussianDistribution.html