InverseLaplaceTransform

InverseLaplaceTransform[F[s],s,t]

给出以 s 为变量的 F[s] 的以 t 为变量的符号拉普拉斯逆变换 f[t].

InverseLaplaceTransform[F[s],s,]

给出数值 处的数值拉普拉斯逆变换.

InverseLaplaceTransform[F[s1,…,sn],{s1,s2,…},{t1,t2,…}]

给出 F[s1,…,sn] 的多维拉普拉斯逆变换.

更多信息和选项

  • 拉普拉斯变换通常用于将微分和偏微分方程转换为代数方程，对方程求解，然后进行逆变换，从而得到解.
  • 拉普拉斯变换还广泛用于控制理论和信号处理，作为以传递函数和传递矩阵的形式表示和操纵线性系统的一种方式. 拉普拉斯变换及其逆变换是时域和频域之间变换的一种方式.
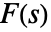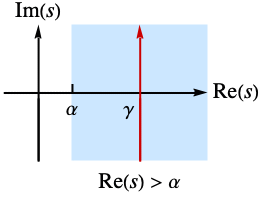
  • 函数 的拉普拉斯逆变换定义成 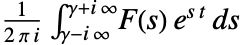，其中 γ 是任意选择的正常数，该常数使得积分的围道位于 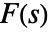的所有奇点的右边.
  • 函数 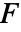的多维拉普拉斯逆变换由形为 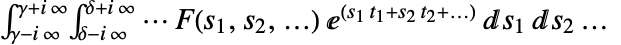的围道积分给出.
  • 如果赋给第三个参数 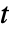的是数值，则使用数值法计算积分. 可用的方法包括："Crump"、"Durbin"、"Papoulis"、"Piessens"、"Stehfest"、"Talbot" 和 "Weeks".
  • 可用 Asymptotic 计算渐近拉普拉斯逆变换.
  • 可给出以下选项：
  • AccuracyGoalAutomatic追求的绝对准确度
    Assumptions$Assumptions对参数的设定
    GenerateConditions False是否给出涉及参数条件的答案
    Method Automatic所用的方法
    PerformanceGoal$PerformanceGoal优化的目标
    PrecisionGoalAutomatic追求的精度
    WorkingPrecisionAutomatic内部计算使用的精度
  • 在 TraditionalForm 中，InverseLaplaceTransform 用 ℒ-1 输出. »

范例

打开所有单元关闭所有单元

基本范例  (4)

计算函数的拉普拉斯逆变换：

含有参数的函数的拉普拉斯逆变换：

绘制结果：

计算数值拉普拉斯逆变换：

二元函数的拉普拉斯逆变换：

范围  (56)

基本用法  (3)

计算符号参数 t 的函数的拉普拉斯逆变换：

使用数值作为参数：

TraditionalForm 格式：

有理函数  (5)

线性函数的倒数：

二次函数的倒数：

逆变换为三角函数的函数：

逆变换为双曲函数的函数：

更多关于有理函数的例子：

初等函数  (5)

含有平方根的函数：

涉及指数和平方根函数的函数：

其他代数函数：

拉普拉斯逆变换的结果是贝塞尔函数：

反正切函数的逆变换：

对数函数  (4)

对数函数的拉普拉斯逆变换：

有理函数的对数：

绘制结果：

对数函数与幂函数的积：

对数函数的平方：

特殊函数  (12)

涉及 BesselK 的函数：

不完全伽马函数与幂函数之比：

多伽玛函数的逆变换：

涉及误差函数的函数的逆变换：

误差函数与平方根函数的复合：

LegendreP 和 LegendreQ 函数的逆变换：

Legendre 函数的辐角图：

BesselI 和 Exp 的积：

频域函数的 ComplexPlot：

BesselJ 和 Gamma 函数的积：

频域函数的 ComplexPlot：

指数积分和平方根函数的组合：

两个 ParabolicCylinderD 函数的积：

涉及椭圆积分函数的逆变换：

EllipticTheta 的逆变换：

分段函数  (5)

下面的函数的逆变换是分段函数：

绘制结果：

下面的指数函数的逆变换是 box 函数：

下面的指数函数的逆变换是分段三角函数：

逆变换的结果是阶梯函数：

更复杂的阶梯函数：

周期函数  (4)

下面的函数的逆变换是关于 t 的周期函数：

激活求和运算：

绘制结果，验证结果是一个方波：

逆变换为正弦函数的绝对值的函数：

激活并绘制结果：

逆变换为梯形波的函数：

更复杂的分段函数的例子：

广义函数  (3)

指数函数的逆变换是 Dirac 函数：

指数函数与 s 的幂函数的积的逆变换是 Dirac 函数的导数：

双曲正割的逆变换是一系列 Dirac 函数：

双曲余切：

多变量函数  (8)

二元有理函数的拉普拉斯逆变换：

验证结果：

关于 p 和 q 的可分离的有理函数：

不能关于 p 和 q 进行分离的有理函数：

逆变换与 BesselJ 有关的有理函数：

含有根式的二元函数的拉普拉斯逆变换：

三变量函数的拉普拉斯逆变换：

有理函数：

含有对数的函数：

数值逆变换  (4)

在一个点上计算拉普拉斯逆变换：

或者，先符号式计算拉普拉斯逆变换：

然后针对 t 的具体值进行计算：

绘制用数值法获得的拉普拉斯逆变换并与精确结果相比较：

逆变换是关于 t 的分段函数：

逆变换是关于 t 的周期函数：

分数阶微积分  (3)

域中代数函数的 ComplexPlot：

该代数函数的拉普拉斯逆变换：

到 -域的拉普拉斯变换：

代数函数的拉普拉斯逆变换：

在时域中绘图：

到 -域的拉普拉斯变换：

涉及参数的代数函数的拉普拉斯逆变换：

到 -域的拉普拉斯变换：

选项  (3)

GenerateConditions  (1)

默认情况下，InverseLaplaceTransform 假定结果是针对非负 t 定义的：

用 GenerateConditions 获取结果有效的范围：

Method  (1)

使用数值运算的默认方法：

用 Method 获取不同方法得到的结果：

Working Precision  (1)

用 WorkingPrecision 获取任意精度的结果：

应用  (5)

计算对应转换函数 的线性系统的步骤：

用拉普拉斯变换求解微分方程：

求解拉普拉斯变换：

求反转换：

应用初值条件：

用 DSolve 直接求解：

求解 3/2 阶分数微分方程：

求拉普拉斯变换：

求逆变换：

绘制解：

用 DSolve 直接求解：

求解 21/10 阶分数微分方程：

求拉普拉斯变换：

求逆变换：

绘制解：

用 DSolve 直接求解：

用 LaplaceTransform 求解分数阶微分方程组：

求逆变换：

属性和关系  (2)

用 Asymptotic 计算渐近近似：

InverseLaplaceTransform 和 LaplaceTransform 是互逆的：

巧妙范例  (2)

一个 MeijerG 函数的 InverseLaplaceTransform：

创建基本的拉普拉斯逆变换表：

Wolfram Research (1999)，InverseLaplaceTransform，Wolfram 语言函数，https://reference.wolfram.com/language/ref/InverseLaplaceTransform.html （更新于 2023 年）.

文本

Wolfram Research (1999)，InverseLaplaceTransform，Wolfram 语言函数，https://reference.wolfram.com/language/ref/InverseLaplaceTransform.html （更新于 2023 年）.

CMS

Wolfram 语言. 1999. "InverseLaplaceTransform." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2023. https://reference.wolfram.com/language/ref/InverseLaplaceTransform.html.

APA

Wolfram 语言. (1999). InverseLaplaceTransform. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/InverseLaplaceTransform.html 年

BibTeX

@misc{reference.wolfram_2025_inverselaplacetransform, author="Wolfram Research", title="{InverseLaplaceTransform}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/InverseLaplaceTransform.html}", note=[Accessed: 03-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_inverselaplacetransform, organization={Wolfram Research}, title={InverseLaplaceTransform}, year={2023}, url={https://reference.wolfram.com/language/ref/InverseLaplaceTransform.html}, note=[Accessed: 03-April-2025 ]}