MatrixPlot
MatrixPlot[m]
行列中の要素の値を視覚的に表すプロットを生成する.
詳細とオプション

- MatrixPlot[m]は,行列が一般的にフォーマットされるのと同じように,デフォルトで m の連続する行をページの下に向けて,連続する列を横に向けて並べる.
- MatrixPlotは,デフォルトで,ゼロ値を白で,負の値を青みがかった色で,正の値を赤みがかった色で表示する.
- MatrixPlotでは,ArrayPlotのオプションに以下の変更を加えたものが使える. [全オプションのリスト]
-
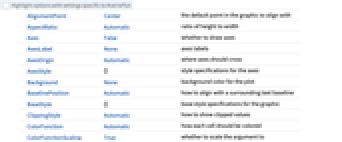
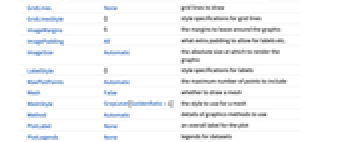
ClippingStyle Automatic 切り取られた値をどのように表示するか Frame True プロットの周囲に枠を描くかどうか FrameTicks All 枠にどのような目盛を入れるか MaxPlotPoints Automatic 含める点の最大数 - PlotRange->r は,-r から+r までの間の aijのみを示すように指定する.
- デフォルト設定のColorFunctionScaling->Trueでは,各行列要素の相対的な値とランキングに基づいてスケーリングが行われる.最終的にスケールされた値は常に0から1の間にあり,スケールされた値0.5が行列要素の値0に相当する.
- デフォルト設定のMaxPlotPoints->Automaticでは,非常に大きいあるいは疎な行列は,MatrixPlotが生成するプロットで構造が見えるようにダウンサンプルされる.
- MatrixPlotはSparseArrayオブジェクトに使うことができる.
全オプションのリスト

例題
すべて開くすべて閉じるスコープ (19)
データ (10)
プレゼンテーション (9)
ColorRulesを使って異なる値を色分けする:
優先順位はColorRulesを高くし,ColorRulesとColorFunctionの両方を使って要素に色付けする:
オプション (33)
Background (2)
ClippingStyle (3)
ColorFunction (5)
ColorDataから名前付きの色勾配を使う:
ColorFunctionScaling (4)
デフォルトで,広い範囲の値の弁別には項目の非線形スケーリングが使われる:
ColorFunctionScaling->Falseとすると項目はスケールされない:
ColorFunctionScaling->Falseとすると,MatrixPlotはArrayPlotのように振る舞う:
ColorFunctionScalingはColorRulesには効果がない:
ColorRules (6)
ColorRulesで任意のパターンを使う:
ColorRulesをColorFunctionとともに使うことができる.優先順位はColorRulesの方が高い:
MaxPlotPoints (1)
デフォルトで,サンプルの大きいおよび/または疎な行列をダウンサンプルするのに自動メソッドが使われる:
MaxPlotPointsのダウンサンプルした値を明示的に設定する:
結果のプロットの視覚的外観もまたColorFunctionの選択の影響を受ける:
PlotRange (3)
特性と関係 (6)
MatrixPlotでは負の項目は寒色,正の項目は暖色になる:
ArrayPlotはグレースケールを使う:
MatrixPlotは広範囲の値を弁別するために行列の項目を再スケールする:
ReliefPlotを医療データや地理データに使う:
連続密度からサンプルされた構造化データと非構造化データにListDensityPlotを使う:
ArrayPlot3Dをデータの3D配列に使う:
GraphPlotを隣接行列の可視化に使う:
考えられる問題 (2)
MaxPlotPointsを使うともとのデータには存在しないアーチファクトが生まれるかもしれない:
MaxPlotPointsオプションの値が小さいと,すべての項目が非零になる:
おもしろい例題 (1)
Sin関数を整数点でプロットする:
テキスト
Wolfram Research (2007), MatrixPlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/MatrixPlot.html (2014年に更新).
CMS
Wolfram Language. 2007. "MatrixPlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/MatrixPlot.html.
APA
Wolfram Language. (2007). MatrixPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MatrixPlot.html