MellinTransform
MellinTransform[expr,x,s]
expr のメリン(Mellin)変換を与える.
MellinTransform[expr,{x1,x2,…},{s1,s2,…}]
expr の多次元メリン変換を与える.
詳細とオプション

- 関数
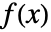 のメリン変換は
のメリン変換は 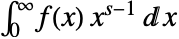 で定義される.
で定義される. - 関数
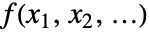 の多次元メリン変換は
の多次元メリン変換は 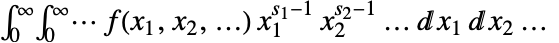 で与えられる.
で与えられる. 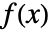 のメリン変換は
のメリン変換は 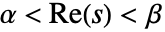 である
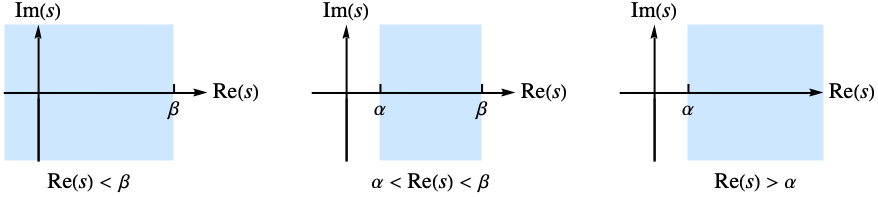
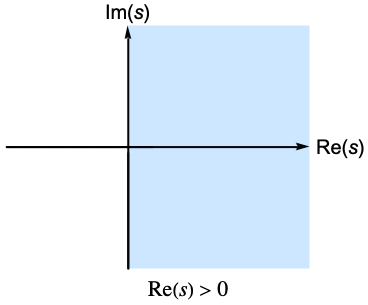
である 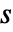 の複素数値についてのみ存在する.この定義が半平面に拡張されることがある.
の複素数値についてのみ存在する.この定義が半平面に拡張されることがある.- 使用可能なオプション
-
Assumptions $Assumptions パラメータについての仮定 GenerateConditions False パラメータについての条件を含む結果を生成するかどうか Method Automatic 使用するメソッド - TraditionalFormでは,MellinTransformは
![TemplateBox[{{f, (, x, )}, x, s}, MellinTransform1] TemplateBox[{{f, (, x, )}, x, s}, MellinTransform1]](Files/MellinTransform.ja/9.png) を使って出力される.
を使って出力される.
例題
すべて開くすべて閉じるスコープ (16)
基本的な用法 (3)
TraditionalFormによる表示:
初等関数 (3)
特殊関数 (3)
区分関数 (3)
一般化された関数 (2)
オプション (5)
GenerateConditions (1)
MellinTransformが与える結果の有効性についての条件を得る:
GenerateConditionsは,この場合はデフォルトでFalseに設定されている:
Method (3)
MeijerGに変換することでこの例の評価を試みても失敗する:
Integrateを通してMellinTransformの定義を使ってこの例を評価する:
この例のデフォルトメソッドではMeijerGへの変換が使われる:
こちらの方が,Integrateを通してMellinTransformの定義を使うよりも速い:
この例はNIntegrateに基づいた数値メソッドで評価される:
アプリケーション (3)
MellinTransformを使って ![]() を評価する.これは,次の関数のメリン変換とみなすことができる:
を評価する.これは,次の関数のメリン変換とみなすことができる:
MellinTransformを各関数に適用する:
Integrateを使って直接積分を計算する:
MellinConvolveを使って同じ結果を得る:
MellinTransformを使ってベッセル方程式の一般解を求める:
MellinTransformを方程式に適用する:
RSolveValueを使って再帰方程式を解く:
InverseMellinTransformを使って必要な一般解を求める:
DSolveValueを使って解を確かめる:
無限級数で定義される関数の漸近展開の最初の2項をMellinTransformを使って求める:
特性と関係 (11)
Asymptoticを使って漸近近似を計算する:
MellinTransformは積分 ![]() を計算する:
を計算する:
Integrateを使って同じ結果を得る:
MellinTransformとInverseMellinTransformは互いに逆関数である:
MellinTransformは線形演算子である:
MellinTransformは![]() によってFourierTransformと関係がある:
によってFourierTransformと関係がある:
考えられる問題 (1)
テキスト
Wolfram Research (2016), MellinTransform, Wolfram言語関数, https://reference.wolfram.com/language/ref/MellinTransform.html.
CMS
Wolfram Language. 2016. "MellinTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MellinTransform.html.
APA
Wolfram Language. (2016). MellinTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MellinTransform.html