Mod
✖
Mod
例題
すべて開くすべて閉じる例 (4)基本的な使用例
スコープ (13)標準的な使用例のスコープの概要
数値評価 (6)
https://wolfram.com/xid/02cbm-s15lus
https://wolfram.com/xid/02cbm-wmfosh
Modは整数に使うことができる:
https://wolfram.com/xid/02cbm-le07m0
https://wolfram.com/xid/02cbm-ccojl6
https://wolfram.com/xid/02cbm-m89
https://wolfram.com/xid/02cbm-ybp
https://wolfram.com/xid/02cbm-c3p
https://wolfram.com/xid/02cbm-10wfg
https://wolfram.com/xid/02cbm-c5gnrk
Modはリストに縫い込まれる:
https://wolfram.com/xid/02cbm-8lqbj9
TraditionalFormによる表示:
https://wolfram.com/xid/02cbm-6fi7x8
記号演算 (7)
https://wolfram.com/xid/02cbm-din
Modを総和で使う:
https://wolfram.com/xid/02cbm-2lbwm8
https://wolfram.com/xid/02cbm-17994q
https://wolfram.com/xid/02cbm-t86bhn
Mod数列を識別する:
https://wolfram.com/xid/02cbm-hixgwa
https://wolfram.com/xid/02cbm-ev808o
https://wolfram.com/xid/02cbm-vjtibo
https://wolfram.com/xid/02cbm-sqc91r
https://wolfram.com/xid/02cbm-flb0zc
アプリケーション (19)この関数で解くことのできる問題の例
基本的なアプリケーション (3)
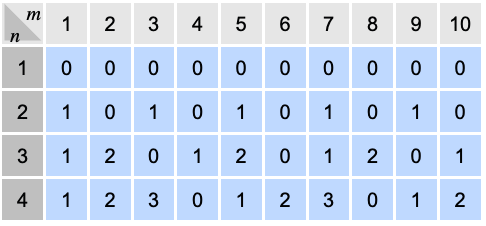
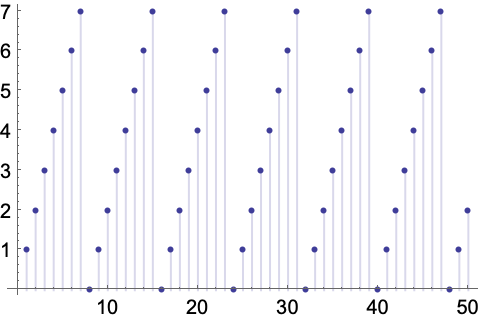
Modの最初の20の値:

https://wolfram.com/xid/02cbm-xwzbqi
https://wolfram.com/xid/02cbm-kbphd2
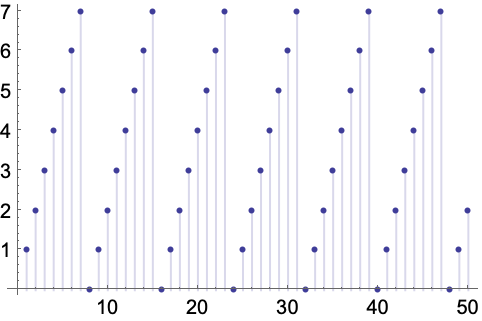
https://wolfram.com/xid/02cbm-b4hvu3
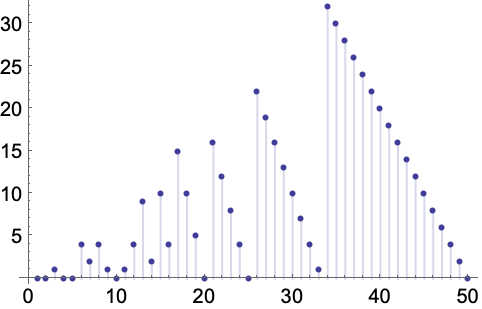
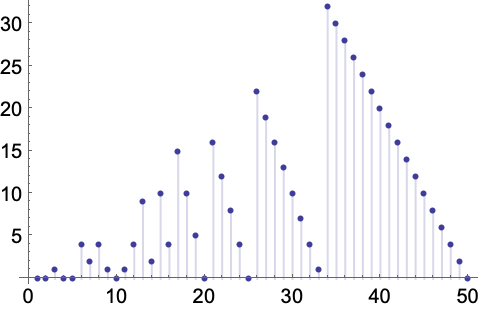
Mod[n,8]の母関数:
https://wolfram.com/xid/02cbm-j0vkps
https://wolfram.com/xid/02cbm-goee5n
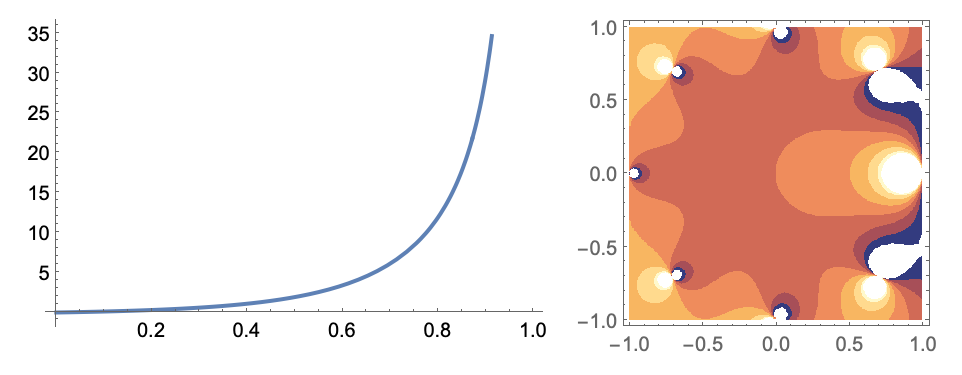
https://wolfram.com/xid/02cbm-7gkxaz
https://wolfram.com/xid/02cbm-5i00ln
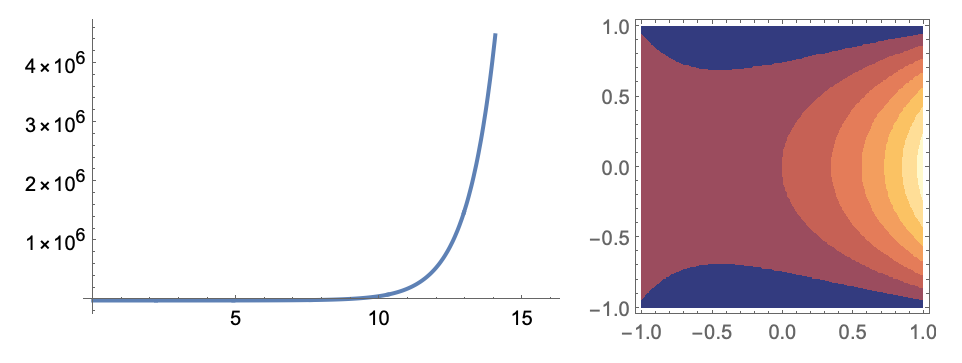
https://wolfram.com/xid/02cbm-sypupo
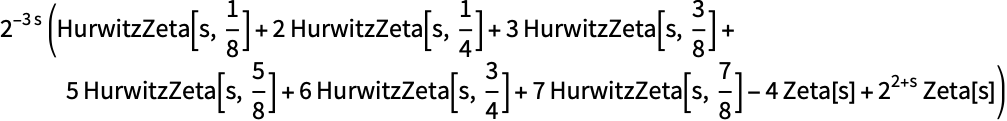
https://wolfram.com/xid/02cbm-4tqu70
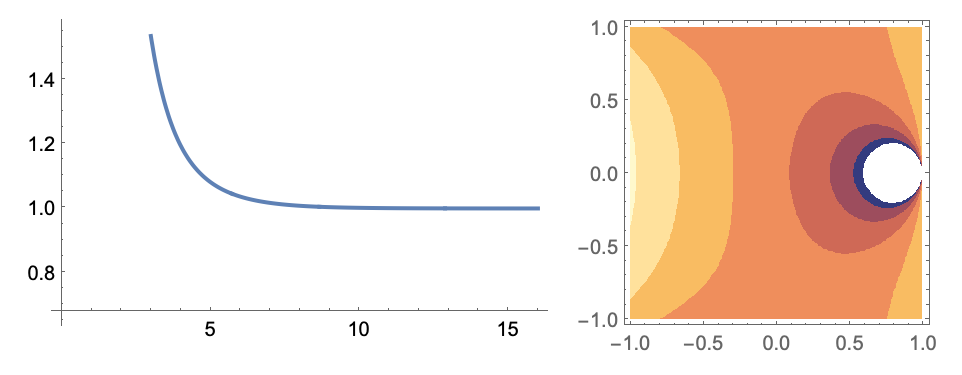
数値識別子 (1)
暗号 (2)
https://wolfram.com/xid/02cbm-b23pum
https://wolfram.com/xid/02cbm-ndudo
https://wolfram.com/xid/02cbm-dqq7e
https://wolfram.com/xid/02cbm-dphnlq
https://wolfram.com/xid/02cbm-esagl5

https://wolfram.com/xid/02cbm-dgtw2
アルファベットの文字をシフトさせてメッセージを暗号化するシーザー暗号をModを使って作る:

https://wolfram.com/xid/02cbm-xwc6ln

https://wolfram.com/xid/02cbm-0laq81
https://wolfram.com/xid/02cbm-gm577x
整数論 (6)
https://wolfram.com/xid/02cbm-00nxhi
https://wolfram.com/xid/02cbm-fcz7g7
https://wolfram.com/xid/02cbm-ts6
https://wolfram.com/xid/02cbm-dzozc8
https://wolfram.com/xid/02cbm-q60cqg
https://wolfram.com/xid/02cbm-1ac4i0
https://wolfram.com/xid/02cbm-wgxdmq
https://wolfram.com/xid/02cbm-yc8
https://wolfram.com/xid/02cbm-vgn
https://wolfram.com/xid/02cbm-qny
Modを使って線形合同式の系を解く:

https://wolfram.com/xid/02cbm-if2ogp
https://wolfram.com/xid/02cbm-5hf4fd
コンピュータサイエンス (3)
https://wolfram.com/xid/02cbm-qx2pgi
https://wolfram.com/xid/02cbm-kvu9y8
https://wolfram.com/xid/02cbm-8c5v1l
https://wolfram.com/xid/02cbm-x36
https://wolfram.com/xid/02cbm-1v1fjw
https://wolfram.com/xid/02cbm-04ubeq
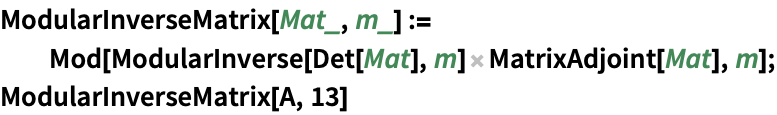
https://wolfram.com/xid/02cbm-z1iqvr
https://wolfram.com/xid/02cbm-1ck8su
政治学,経済学,社会学 (2)
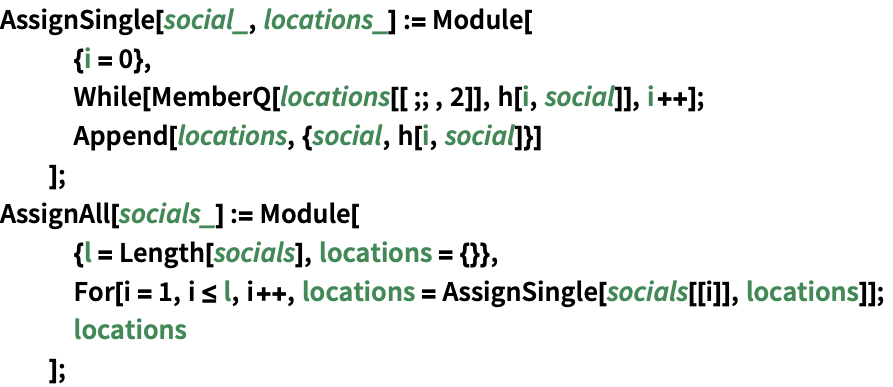
ハッシュアルゴリズムに基づいて(アメリカ合衆国の)社会保障番号にメモリアドレスを割り当てる:
https://wolfram.com/xid/02cbm-0yqjhn
各社会保障番号に場所を,衝突がないことを確認して割り当てる:
https://wolfram.com/xid/02cbm-3cycsr
https://wolfram.com/xid/02cbm-1jqepr
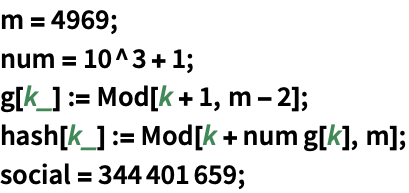
https://wolfram.com/xid/02cbm-xgcgio
https://wolfram.com/xid/02cbm-8pxpjb
その他のアプリケーション (2)
特性と関係 (7)この関数の特性および他の関数との関係
Modは周期関数である:
https://wolfram.com/xid/02cbm-ud8amv
Modはすべての複素数上で定義される:
https://wolfram.com/xid/02cbm-ctu0mc
https://wolfram.com/xid/02cbm-pqywiy
Modは推移的である.もし ![]() かつ
かつ ![]() なら
なら ![]() である:
である:
https://wolfram.com/xid/02cbm-i1dp6y
https://wolfram.com/xid/02cbm-tssupn
https://wolfram.com/xid/02cbm-lqnk95
https://wolfram.com/xid/02cbm-bk0r6w
https://wolfram.com/xid/02cbm-rhv2h3
QuotientRemainder[a,n]はMod[a,n]と同じである:
https://wolfram.com/xid/02cbm-jllr0w
https://wolfram.com/xid/02cbm-fp5d3g
PowerModを使って逆モジュロを計算する:
https://wolfram.com/xid/02cbm-jvgwab
https://wolfram.com/xid/02cbm-d8q8jd
https://wolfram.com/xid/02cbm-mfn
https://wolfram.com/xid/02cbm-di3
正の実数 x について,Mod[x,1]は x の小数部分を与える:
https://wolfram.com/xid/02cbm-wwuhnq
https://wolfram.com/xid/02cbm-60ycn2
考えられる問題 (1)よく起る問題と予期しない動作
計算によってはデフォルトよりも高い内部精度を要求するものがある:
https://wolfram.com/xid/02cbm-xih
$MaxExtraPrecisionの値をリセットする:
https://wolfram.com/xid/02cbm-itv

おもしろい例題 (4)驚くような使用例や興味深い使用例
https://wolfram.com/xid/02cbm-g1u

https://wolfram.com/xid/02cbm-tj7
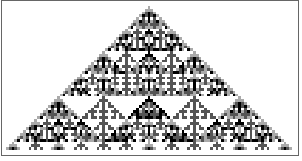
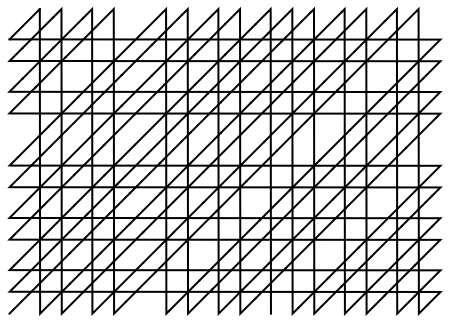
49を法として合同に基づいて彩色された数でウラム(Ulam)の螺線をプロットする:

https://wolfram.com/xid/02cbm-zp3c6
https://wolfram.com/xid/02cbm-qhm0kv

https://wolfram.com/xid/02cbm-nmlpvs

Wolfram Research (1988), Mod, Wolfram言語関数, https://reference.wolfram.com/language/ref/Mod.html (2002年に更新).テキスト
Wolfram Research (1988), Mod, Wolfram言語関数, https://reference.wolfram.com/language/ref/Mod.html (2002年に更新).
Wolfram Research (1988), Mod, Wolfram言語関数, https://reference.wolfram.com/language/ref/Mod.html (2002年に更新).CMS
Wolfram Language. 1988. "Mod." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2002. https://reference.wolfram.com/language/ref/Mod.html.
Wolfram Language. 1988. "Mod." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2002. https://reference.wolfram.com/language/ref/Mod.html.APA
Wolfram Language. (1988). Mod. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Mod.html
Wolfram Language. (1988). Mod. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Mod.htmlBibTeX
@misc{reference.wolfram_2025_mod, author="Wolfram Research", title="{Mod}", year="2002", howpublished="\url{https://reference.wolfram.com/language/ref/Mod.html}", note=[Accessed: 01-April-2025
]}BibLaTeX
@online{reference.wolfram_2025_mod, organization={Wolfram Research}, title={Mod}, year={2002}, url={https://reference.wolfram.com/language/ref/Mod.html}, note=[Accessed: 01-April-2025
]}