MultivariateTDistribution

MultivariateTDistribution[Σ,ν]

尺度行列 Σ，自由度のパラメータ ν の多変量スチューデント 分布を表す．

MultivariateTDistribution[μ,Σ,ν]

位置 μ，尺度行列 Σ，自由度 ν の多変量スチューデント 分布を表す．

詳細

  • 多変量 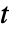分布におけるベクトル 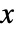の確率密度は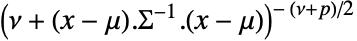に比例する．ただし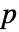， は 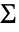の長さである．
  • 多変量スチューデント 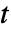分布は変量間の多変量正規分布と共分散の割合を特徴付ける．
  • MultivariateTDistributionでは，Σ は任意の実数の 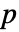× 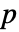正定値対称行列でよく，μ は任意の実ベクトルでよい．ただし，p=Length[μ] であり ν は任意の正の実数である．
  • これは，ベクトル μ と共分散行列 Σ が μ⊗μ と Σ が成分ごとに同じ単位次元を持つような数量でよく，ν が無次元量でよいことを示している． »
  • MultivariateTDistributionは，Mean，CDF，RandomVariate等の関数とともに使うことができる．

予備知識

  • MultivariateTDistribution[μ,Σ,ν]は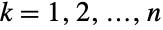， について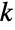， 番目の各（一変量）周辺分布がStudentTDistributionであるという特性によって特徴付けられた 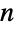個のタプル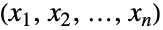すべての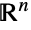の集合上でサポートされた多変量連続統計分布を表す．表現を変えるなら，各変量 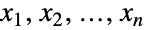は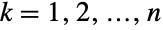， について xkStudentTDistributionを満足する．多変量 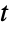分布は，正の実数 ν （分布の自由度を示す），実数のベクトル μ （分布の「位置」と呼ばれる），正定値対称行列 Σ （「尺度行列」と呼ばれる）によってパラメータ化される．これらは，nLength[μ]Length[Σ]を満足し，分布の陪平均，分散，共分散を定義する．2引数形のMultivariateTDistribution[Σ,ν]はMultivariateTDistribution[{0,…,0},Σ,ν]に等しく，中心（あるいは中心化）多変量 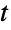分布と呼ばれることがある．
  • 多変量 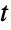分布の確率密度関数(PDF)は単一の絶対最大値を持つが，複数の「峰」（相対的最大値）を持つことがある．一般に，同伴周辺分布のPDFは，周辺分布のPDFが 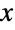の大きい値について指数的というよりむしろ代数的に減少するという意味で「太い」（この動作は周辺分布のSurvivalFunctionを分析することで数量的に厳密にすることができる）．
  • 多変量 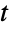分布は多変量正規分布と変量間の共分散の比として特徴付けられる．歴史的に，同じ特徴を持つがここで実装されているものとは異なる数多くの候補となる分布が定義されてきた．上で定義された多変量 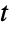分布は多変量ベイズ解析における不可欠のツールであり，多変量正規分布の事後分布として，あるいは特定の多変量回帰モデルにおける回帰係数ベクトルの周辺事後分布として等を含むさまざまなコンテキストで使われている．このため，多変量 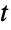分布はベイズ推論と関連した多くのアプリケーションに使われており，ポートフォリオの最適化，判別式，クラスタ解析，多重決定問題を含むさまざまなコンテキストにおけるツールとしても使われている．
  • RandomVariateを使って，多変量 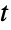分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,MultivariateTDistribution[μ,Σ,ν]] （より簡略な表記では xMultivariateTDistribution[μ,Σ,ν]）を使って，確率変数 x が多変量 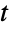分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • 多変量 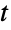分布の確率密度関数および累積分布関数は，PDF[MultivariateTDistribution[μ,Σ,ν],{x1,x2,…,xn}]およびCDF[MultivariateTDistribution[μ,Σ,ν],{x1,x2,…,xn}]を使って得られることがある．平均，中央値，分散，共分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Covariance，Moment，CentralMomentを使って計算することができる．
  • DistributionFitTestを使って，与えられたデータ集合が多変量 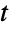分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからパラメトリック多変量 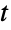分布を推定することが，FindDistributionParametersを使ってデータを多変量 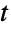分布にフィットすることができる．ProbabilityPlotを使って記号多変量 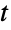分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使って記号多変量 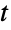分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換された多変量 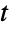分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使って多変量 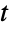分布含む高次元分布を構築することが，ProductDistributionを使って多変量 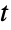分布を含む独立成分分布の結合分布を計算することができる．
  • MultivariateTDistributionは数多くの他の分布と関連がある．MultivariateTDistributionは，上で説明したように，StudentTDistributionと関係があり，MultivariateTDistributionの一次元周辺分布がStudentTDistributionに従うのに対し，周辺分布のそれぞれはMultivariateTDistributionの例となっている． MultivariateTDistributionは，ν∞におけるPDF[MultivariateTDistribution[{μ1,μ2},{{1,ρ},{ ρ,1}},ν],{x,y}]の極限がPDF[MultinormalDistribution[{μ1,μ2},{{1,ρ},{ ρ,1}}],{x,y}]と厳密に等しいという意味で，MultinormalDistributionの極限である．また，MultivariateTDistributionはMultinormalDistributionとの関係のためにTransformedDistributionを介してLogMultinormalDistributionと関連している．MultivariateTDistributionは，一変量StudentTDistributionとの関係のために，NoncentralStudentTDistribution，FRatioDistribution，NormalDistribution，HalfNormalDistribution，LogNormalDistribution，PearsonDistribution，CauchyDistribution，ChiSquareDistributionとも関連している．

例題

すべて開くすべて閉じる

例  (4)

確率密度関数：

累積分布関数：

平均と分散：

共分散：

スコープ  (9)

二変量 分布から擬似確率ベクトルのサンプルを生成する：

ヒストグラムを使ってサンプルを可視化する：

分布母数推定：

サンプルデータから分布母数を推定する：

適合度検定：

歪度：

定義されている場合は歪度は常に0である：

尖度：

尖度は自由度のみに依存する：

自由度が に近付くにつれ，尖度はMultinormalDistributionの尖度に近付く：

二変量 分布の相関：

標準二変量 分布のさまざまな混合モーメント：

混合中心モーメント：

混合階乗モーメント：

混合キュムラント：

ハザード関数：

周辺分布はStudentTDistributionに従う：

母数でQuantityを一貫して使うとQuantityDistributionが与えられる：

アプリケーション  (3)

分布関数とそのヒストグラムを同じプロットで示す：

確率密度関数とそのヒストグラムを比較する：

累積分布関数とそのヒストグラムを比較する：

多変量スチューデント 分布はコピュラ分布の定義に使われる：

確率密度関数：

平均と分散：

乱数を生成する：

幾何ブラウン運動でモデル化された株価は，対数利益率において正規分布に従うとみなされる．以下で，2015年におけるGOOG，MSFT，FB，AAPL，INTCの5社の株価を検討する：

対数利益率を計算する：

MultinormalDistributionにデータをフィットし，KolmogorovSmirnovTestを実行する：

データをMultivariateTDistributionにフィットし，同じ検定を行う：

特性と関係  (6)

二変量 分布の等確率の等高線：

多変量スチューデント 分布はアフィン変換のもとで閉じている：

アフィン変換は分布次元を保存する必要はない：

他の分布との関係：

多変量正規分布は ν が に近付く際のMultivariateTDistributionの極限である：

デフォルトの位置は0である：

MultivariateTDistributionは多変量Tカーネルとスチューデント 周辺分布を持つCopulaDistributionに等しい：

考えられる問題  (2)

Σ が正定値対称行列でなければMultivariateTDistributionは定義されない：

ν が正でなければMultivariateTDistributionは定義されない：

無効な母数を記号出力に代入すると意味のない結果が返される：

おもしろい例題  (1)

さまざまな相関の確率密度関数：

Wolfram Research (2010), MultivariateTDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/MultivariateTDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2010), MultivariateTDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/MultivariateTDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2010. "MultivariateTDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/MultivariateTDistribution.html.

APA

Wolfram Language. (2010). MultivariateTDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MultivariateTDistribution.html

BibTeX

@misc{reference.wolfram_2024_multivariatetdistribution, author="Wolfram Research", title="{MultivariateTDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MultivariateTDistribution.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_multivariatetdistribution, organization={Wolfram Research}, title={MultivariateTDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/MultivariateTDistribution.html}, note=[Accessed: 22-November-2024 ]}