WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

NearestNeighborG[pdata,r]

点データ pdata 内の半径 r にある最近傍関数 を推定する．

NearestNeighborG[pproc,r]

点過程 pproc について を計算する．

NearestNeighborG[bdata,r]

ビン分割データ bdata について を計算する．

NearestNeighborG[pspec]

異なる半径 r に繰り返し適用可能な関数 を生成する．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
点データ  
点過程  
オプション  
SpatialBoundaryCorrection  
アプリケーション  
特性と関係  
関連項目
関連するガイド
履歴
引用書式

NearestNeighborG

NearestNeighborG[pdata,r]

点データ pdata 内の半径 r にある最近傍関数 を推定する．

NearestNeighborG[pproc,r]

点過程 pproc について を計算する．

NearestNeighborG[bdata,r]

ビン分割データ bdata について を計算する．

NearestNeighborG[pspec]

異なる半径 r に繰り返し適用可能な関数 を生成する．

詳細とオプション

  • NearestNeighborGは，最近傍関数および最近傍分布としても知られている．
  • 関数 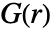は，pdata または pproc のどちらかの中で，典型的な点の距離 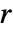内で別の点が見付かる確率を与える．
  •     
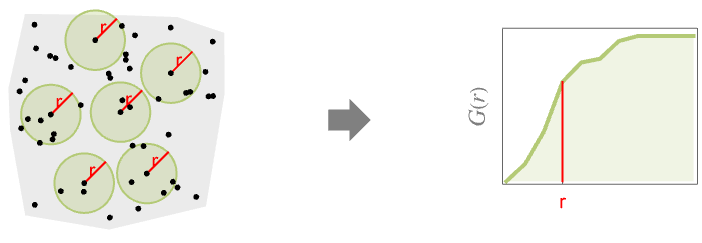
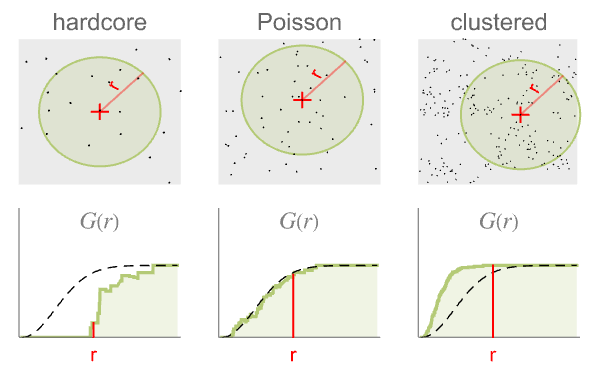
  • ポアソン(Poisson)点過程と比較すると，結果は以下のようになる．
  •     
  • 半径 r は単一の値でも値のリストでもよい．半径 r が指定されていないと，NearestNeighborGはPointStatisticFunctionを返す．これを使って 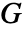関数を繰り返し評価することができる．
  • 点 pdata は次の形式でよい．
  • {p1,p2,…}点 pi
    GeoPosition[…],GeoPositionXYZ[…],…グラフィックスの点
    SpatialPointData[…]空間点の集合
    {pts,reg}点集合 pts と観測領域 reg
  • 観測領域 reg は，与えられていなければRipleyRassonRegionを使って自動的に計算される．
  • 点過程 pproc は次の形式でよい．
  • proc点過程 proc
    {proc,reg}点過程 proc と観測領域 reg
  • 観測領域 reg は，パラメータを持たずSpatialObservationRegionQでなければならない．
  • ビン分割データ bdata はSpatialBinnedPointDataからのもので，区分定強度関数でInhomogeneousPoissonPointProcessとして扱われる．
  • pdata について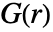，は観測領域を離散化することで計算され，一定の点強度を仮定している．
  • pproc について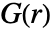，は厳密な式で，あるいはシミュレーションを使って点データを生成して計算される．
  • 次は，使用可能なオプションである．
  • MethodAutomatic使用するメソッド
    SpatialBoundaryCorrection Automatic使用する境界補正
  • SpatialBoundaryCorrectionには次の設定を使うことができる．
  • Automatic自動決定された境界補正
    None境界補正なし
    "BorderMargin"観測領域に内部余白を使う
    "Hanisch"最近傍までの距離が境界までの距離よりも大きい点を削除する
    "KaplanMeier"SurvivalDistribution法．最近傍までの点距離が境界領域で打ち切られる
    "NelsonAalen"SurvivalDistribution法．最近傍までの点距離が領域境界で打ち切られる
  • Method->{"Discretization"->opts}の設定では推定における離散化メソッドが調整される．ここでは，opts はDiscretizeRegionの任意の有効なオプションでよい．

例題

すべて開く すべて閉じる

例  (3)

最近傍関数を指定の距離で推定する：

Wolfram Language code: region = Ball[{0, 0}]; pts = RandomPoint[region, 100];
Wolfram Language code: NearestNeighborG[{pts, region}, 0.1]

最近傍関数を距離範囲内で推定する：

Wolfram Language code: spd = SpatialPointData[RandomReal[1, {100, 2}]]
Wolfram Language code: rspec = Range[0.01, 0.2, 0.01];
Wolfram Language code: est = NearestNeighborG[spd, rspec];

結果をListPlotで可視化する：

Wolfram Language code: ListPlot[est, DataRange -> MinMax[rspec], AxesLabel -> {r}, Filling -> Axis]

クラスタ点過程の空空間関数：

Wolfram Language code: f = NearestNeighborG[MaternPointProcess[3, 2, 0.2, 2], r];
Wolfram Language code: Plot[f, {r, 0, 0.5}, AxesLabel -> Automatic]

スコープ  (8)

点データ  (5)

最近傍関数を距離0.1で推定する：

Wolfram Language code: region = Rectangle[{0, 0}, {1, 2}]; pts = RandomPoint[region, 100];
Wolfram Language code: NearestNeighborG[{pts, region}, 0.1]

与えられた距離のリストについて最近傍関数の経験的推定を得る：

Wolfram Language code: NearestNeighborG[{pts, region}, {0.1, 0.15, 0.01, 0.03}]

NearestNeighborGをSpatialPointDataと一緒に使う：

Wolfram Language code: spd = SpatialPointData[RandomReal[1, {500, 3}]]
Wolfram Language code: res = NearestNeighborG[spd, {0.01, 0.02}]

後で使うためにPointStatisticFunctionを作成する：

Wolfram Language code: reg = Disk[]; pts = RandomPoint[Disk[], 100];
Wolfram Language code: psf = NearestNeighborG[{pts, reg}]

指定された半径で関数を評価する：

Wolfram Language code: psf[0.02]

明示的に観測領域を与えることなしに最近傍関数を推定する：

Wolfram Language code: BlockRandom[SeedRandom[1]; pts = RandomReal[1, {100, 2}] ];
Wolfram Language code: psf = NearestNeighborG[pts]

Ripley–Rasson推定器で生成された観測領域：

Wolfram Language code: psf["ObservationRegion"]

距離0.05で 関数を推定する：

Wolfram Language code: psf[0.05]

NearestNeighborGをGeoPositionと一緒に使う：

Wolfram Language code: pts = RandomGeoPosition[GeoDisk[GeoPosition[{0, 0}], Quantity[10, "Kilometers"]], 10 ^ 2]
Wolfram Language code: psf = NearestNeighborG[pts]

点統計関数をプロットする：

Wolfram Language code: ListPlot[Table[{x, psf[x]}, {x, Quantity[0, "km"], psf["MaxRadius"], Quantity[.1, "km"]}], AxesLabel -> {"km"}]

点過程  (3)

PoissonPointProcessの最近傍関数は閉じた形をしている：

Wolfram Language code: proc = PoissonPointProcess[μ, d];
Wolfram Language code: NearestNeighborG[proc, r]

固定強度と変化する次元について可視化する：

Wolfram Language code: Plot[Table[NearestNeighborG[proc /. μ -> 2, r], {d, 1, 4}]//Evaluate, {r, 0, 1.3}, AxesLabel -> Automatic, PlotLegends -> (Row[{#, "D"}]& /@ Range[4])]

指定次元のクラスタ過程ThomasPointProcessの最近傍関数：

Wolfram Language code: proc2D = ThomasPointProcess[20, 10, .05, 2];
Wolfram Language code: DiscretePlot[NearestNeighborG[proc2D, r], {r, 0.01, .5, .02}, PlotRange -> {0, 1}, AxesLabel -> Automatic]

3Dで：

Wolfram Language code: proc3D = ThomasPointProcess[20, 10, .05, 3];
Wolfram Language code: DiscretePlot[NearestNeighborG[proc3D, r], {r, 0.01, .5, .02}, PlotRange -> {0, 1}, AxesLabel -> Automatic]

指定次元のクラスタ過程MaternPointProcessの最近傍関数：

Wolfram Language code: proc2D = MaternPointProcess[30, 5, 1, 2];
Wolfram Language code: DiscretePlot[NearestNeighborG[proc2D, r], {r, 0.01, .5, .02}, PlotRange -> {0, 1}, AxesLabel -> Automatic]

3Dで：

Wolfram Language code: proc3D = MaternPointProcess[30, 5, 1, 3];
Wolfram Language code: DiscretePlot[NearestNeighborG[proc3D, r], {r, 0.01, .5, .02}, PlotRange -> {0, 1}, AxesLabel -> Automatic]

オプション  (2)

SpatialBoundaryCorrection  (2)

境界補正がないNearestNeighborG推定器には偏りがあるので，大きい点集合以外で使うべきではない：

Wolfram Language code: region = Rectangle[{0, 0}, {1, 2}]; pts = RandomPoint[region, 100];
Wolfram Language code: NearestNeighborG[{pts, region}, 0.1, SpatialBoundaryCorrection -> "None"]

デフォルトメソッドの"BorderMargin"は境界から の距離にある点だけを考慮する：

Wolfram Language code: NearestNeighborG[{pts, region}, 0.1, SpatialBoundaryCorrection -> "BorderMargin"]

"Hanisch"法は観測領域の各点に重みを付けて推定した値が偏らないようにする：

Wolfram Language code: NearestNeighborG[{pts, region}, 0.1, SpatialBoundaryCorrection -> "Hanisch"]

"KaplanMeier"法と"NelsonAalen"法はSurvivalDistributionで使われる推定器である．各点からその点の最近傍点までの距離は各点から観測領域の境界までの距離によって打ち切られる：

Wolfram Language code: NearestNeighborG[{pts, region}, 0.1, SpatialBoundaryCorrection -> "KaplanMeier"]
Wolfram Language code: NearestNeighborG[{pts, region}, 0.1, SpatialBoundaryCorrection -> "NelsonAalen"]

異なる辺補正メソッドを比較する：

Wolfram Language code: region = Ball[{0, 0, 0}]; pts = RandomPoint[region, 400];

最近傍関数の値を異なる3つの方法で推定する：

Wolfram Language code: rlist = Range[0.01, 0.3, 0.01]; mths = {"BorderMargin", "Hanisch", "KaplanMeier"};
Wolfram Language code: data = NearestNeighborG[{pts, region}, rlist, SpatialBoundaryCorrection -> #]& /@ mths;

結果を可視化する：

Wolfram Language code: f[r_] := 1 - Exp[-(400 / RegionMeasure[region])(4Pi / 3)r ^ 3];
Wolfram Language code: Show[Plot[f[r], {r, 0, 0.3}, PlotStyle -> Gray, PlotLegends -> {"theoretical"}], ListPlot[data, DataRange -> MinMax[rlist], PlotLegends -> mths], AxesLabel -> {r}]

アプリケーション  (5)

空間的にランダムなデータの最近傍関数：

Wolfram Language code: data1 = RandomPointConfiguration[PoissonPointProcess[50, 2], Disk[]]; data2 = RandomPointConfiguration[InhomogeneousPoissonPointProcess[Function[{x, y}, (40x ^ 2 + 80y ^ 2)], 2], Disk[]];

結果を可視化する：

Wolfram Language code: G1 = NearestNeighborG[data1]; G2 = NearestNeighborG[data2];
Wolfram Language code: Plot[{G1[r], G2[r]}, {r, 0, 1 / 2}, PlotRange -> All, AxesLabel -> {r}]

ハードコアデータのための空空間関数：

Wolfram Language code: rr = {0.05, 0.1, 0.15}; spds = Table[RandomPointConfiguration[HardcorePointProcess[100, rad, 2], Disk[]], {rad, rr}];

空空間関数の値を与えられたデータで推定する：

Wolfram Language code: Gs = Table[NearestNeighborG[spd], {spd, spds}];

結果を可視化する：

Wolfram Language code: DiscretePlot[Map[#[r]&, Gs]//Evaluate, {r, 0.005, 0.2, 0.005}, AxesLabel -> {r}, PlotLegends -> (Row[{"rad = ", #}]& /@ rr)]

ランシング(Lansing)の森でリスが木から木へと跳び移る際の平均距離はNearestNeighborGを使って計算できる：

Wolfram Language code: data = ResourceData["Sample Data: Lansing Woods"]
Wolfram Language code: nnG = NearestNeighborG[data]; maxR = nnG["MaxRadius"];
Wolfram Language code: DiscretePlot[nnG[r], {r, maxR / 100, maxR, maxR / 50}]

典型的な点とその最近傍点との平均距離（正のサポート分布の場合は1-累積分布関数のリーマン和で近似可能）：

Wolfram Language code: step = maxR / 100; partition = Table[{k, k + step}, {k, 0, maxR, step}]; values = nnG[Mean /@ partition];
Wolfram Language code: Total[(1 - values) * step]

場所の集合を結ぶのに必要なケーブルの最短の長さの平均を計算する：

Wolfram Language code: near𝒟 = ProbabilityDistribution[{CDF, NearestNeighborG[PoissonPointProcess[3, 2], r]}, {r, 0, ∞}]
Wolfram Language code: count𝒟 = PointCountDistribution[PoissonPointProcess[3, 2], Rectangle[]]
Wolfram Language code: cable𝒟 = TransformedDistribution[(n - 1) * r, {rnear𝒟, ncount𝒟}]
Wolfram Language code: Mean[cable𝒟]

既存のデータによって地震の確率を分析する：

Wolfram Language code: region = Entity["AdministrativeDivision", {"California", "UnitedStates"}]["Polygon"];
Wolfram Language code: es = EarthquakeData[region, 5, {{1600, 1, 1}, {2017, 1, 1}}, "Position"]

場所を抽出する：

Wolfram Language code: data = Normal[es["Values"]];
Wolfram Language code: GeoGraphics[{Orange, region, Darker@Red, Point[data]}]

歴史的な地震発生地から10マイル以内で別の地震が起こる確率：

Wolfram Language code: NearestNeighborG[{data, region}, Quantity[10, "Miles"]]

確率を可視化する：

Wolfram Language code: Plot[NearestNeighborG[{data, region}, Quantity[r, "Miles"]], {r, 1, 10}, PlotPoints -> 2, AxesLabel -> {r}]

特性と関係  (2)

NearestNeighborGはしばしばEmptySpaceFと比較されるが，後者は参照点から距離 r 以内で別の点が見付かる確率を推定する：

Wolfram Language code: region = Ball[{0, 0}]; spd = RandomPointConfiguration[PoissonPointProcess[100, 2], region]
Wolfram Language code: rspec = Range[0, 0.15, 0.005]; res = EmptySpaceF[spd, rspec];

EmptySpaceFは適切なCDFである：

Wolfram Language code: ListPlot[res, DataRange -> MinMax[rspec], Filling -> Axis, AxesLabel -> {r}]

HardcorePointProcessによって生成された点データについてのNearestNeighborGとEmptySpaceFの間の推定を比較する：

Wolfram Language code: spd1 = RandomPointConfiguration[HardcorePointProcess[500, 0.15, 2], region]
Wolfram Language code: rspec1 = Range[0, 0.3, 0.01]; esf = EmptySpaceF[spd1, rspec1]; nng = NearestNeighborG[spd1, rspec1];
Wolfram Language code: ListLinePlot[{esf, nng}, DataRange -> MinMax[rspec1], Filling -> Axis, AxesLabel -> {r}, PlotLegends -> {"Empty Space Distribution", "Nearest Neighbor Distribution"}]

PoissonPointProcessの空空間関数と最近傍関数は同じである：

Wolfram Language code: proc = PoissonPointProcess[μ, d];
Wolfram Language code: EmptySpaceF[proc, r]
Wolfram Language code: NearestNeighborG[proc, r]
Wolfram Language code: %% - %

どちらもExponentialDistributionの累積密度分布に等しい：

Wolfram Language code: Clear[vol]; vol[d_, r_] := π ^ (d / 2) / Gamma[1 + d / 2]r ^ d;
Wolfram Language code: CDF[ExponentialDistribution[μ * vol[d, r] / r], r]
Wolfram Language code: % == EmptySpaceF[proc, r] == NearestNeighborG[proc, r]//Refine[#, r > 0]&
Wolfram Research (2020), NearestNeighborG, Wolfram言語関数， https://reference.wolfram.com/language/ref/NearestNeighborG.html.

テキスト

Wolfram Research (2020), NearestNeighborG, Wolfram言語関数， https://reference.wolfram.com/language/ref/NearestNeighborG.html.

CMS

Wolfram Language. 2020. "NearestNeighborG." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NearestNeighborG.html.

APA

Wolfram Language. (2020). NearestNeighborG. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NearestNeighborG.html

BibTeX

@misc{reference.wolfram_2026_nearestneighborg, author="Wolfram Research", title="{NearestNeighborG}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/NearestNeighborG.html}", note=[Accessed: 06-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_nearestneighborg, organization={Wolfram Research}, title={NearestNeighborG}, year={2020}, url={https://reference.wolfram.com/language/ref/NearestNeighborG.html}, note=[Accessed: 06-November-2026]}