ParetoDistribution

ParetoDistribution[k,α]

最小値母数 k，形状母数 α のパレート分布を表す．

ParetoDistribution[k,α,μ]

位置母数 μ のパレート分布タイプIIを表す．

ParetoDistribution[k,α,γ,μ]

形状母数 γ のパレート分布タイプIVを表す．

詳細

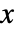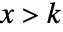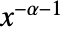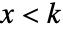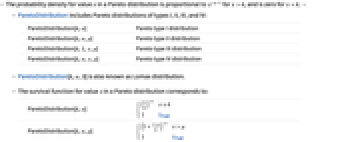
  • パレート分布における値 の確率密度は， のときは に比例し， のときは0である． »
  • ParetoDistributionにはタイプI，タイプII，タイプIII，タイプIVのパレート分布が含まれる．
  • ParetoDistribution[k,α]タイプIのパレート分布
    ParetoDistribution[k,α,μ]タイプIIのパレート分布
    ParetoDistribution[k,1,γ,μ]タイプIIIのパレート分布
    ParetoDistribution[k,α,γ,μ]タイプIVのパレート分布
  • ParetoDistribution[k,α,0]はLomax分布としても知られている．
  • パレート分布における値 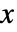の生存関数は以下に対応する．
  • ParetoDistribution[k,α](x/k)^(-alpha) x>=k; 1 TemplateBox[{True, paclet:ref/True}, RefLink, BaseStyle -> {2ColumnTableMod}]
    ParetoDistribution[k,α,μ](1+(x-mu)/k)^(-alpha) x>mu; 1 TemplateBox[{True, paclet:ref/True}, RefLink, BaseStyle -> {2ColumnTableMod}]
    ParetoDistribution[k,α,γ,μ](1+((x-mu)/k)^(1/gamma))^(-alpha) x>mu; 1 TemplateBox[{True, paclet:ref/True}, RefLink, BaseStyle -> {2ColumnTableMod}]
  • ParetoDistributionでは，α，k，γ は任意の正の実数でよく，μ は任意の実数でよい．
  • ParetoDistributionでは，k と μ は単位次元が等しい任意の数量でよく，α と γ は無次元量でよい． »
  • ParetoDistributionは，Mean，CDF，RandomVariate等の関数とともに使うことができる． »

予備知識

  • ParetoDistributionは，その引数構造によって，タイプIからタイプIVまでの4つのタイプのいずれに属するかが決まる，統計的分布を表す．パレート分布の確率密度関数(PDF)の全体的な形は，引数によって大きく変わる．例えば，タイプIおよびタイプIIのパレート分布のPDFは単調減少であるのに対し，タイプIVの分布は単一の峰を持つことがある．これに加えて，ParetoDistributionの全タイプのPDFは，半無限区間上で定義され，PDFの裾部はPDFが 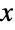の大きい値について指数的に減少するのではなく，むしろベキ法則として減少するという意味で「太って」いる．（この動作は，分布のSurvivalFunctionを解析することで，数量的に厳密にすることができる．）
  • パレート分布は，庭に植えてあるエンドウ豆のほぼ8割がおよそ2割のエンドウ豆の鞘から得られたものだということに気付いた，イタリアの経済学者ヴィルフレド・パレートから始まったものである．後に，パレートは国家間の富の分布が同様の分布に従うという観察を得た．この結果から，彼はいわゆるいわゆる80:20の法則（パレートの法則）を開発した．このもとになるのが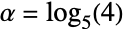でParetoDistribution[k,α]に対応するタイプIのパレート分布である．パレート分布は，この他の多くの数学および科学的な状況にも見られ，ハードディスクのエラー率，株式の利益．ボース・アインシュタイン統計等を含む現象に適用可能である．
  • RandomVariateを使って，パレート分布から1つあるいは複数の機械精度あるいは任意精度の（後者はWorkingPrecision オプションによる）擬似乱数変量を与えることができる．Distributed[x,ParetoDistribution[k,α]]（より簡略な表記では xParetoDistribution[k,α]）を使って，確率変数 x がタイプIのパレート分布に従って分布していると宣言することができる．正の母数 α はパレート指標として知られている．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で用いることができる．
  • タイプIのパレート分布についての確率密度関数および累積分布関数は，PDF[ParetoDistribution[k,α]],x]およびCDF[ParetoDistribution[k,α]],x]を使ってそれぞれ得ることができる．タイプII，III，IVのパレート分布についても同様の式がある．一般に，パレート分布には 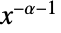に比例するPDFがある．平均，中央値，分散，原点の周りのモーメント，中心モーメントはそれぞれ，Mean，Median，Variance，Moment，CentralMomentを使って計算することができる．
  • DistributionFitTestを使って，与えられたデータ集合がパレート分布と一致するどうかを検定することが，EstimatedDistributionを使って，与えられたデータからパレートパラメトリック分布を推定することが，FindDistributionParametersを使って，データをパレート分布にフィットすることが可能である．ProbabilityPlotを使って記号パレート分布のCDFに対する与えられたデータのCDFプロットを生成することができ，QuantilePlotを使って記号パレート分布の変位値に対する与えられたデータの分位点プロットを生成することができる
  • TransformedDistributionを使って変換されたパレート分布を，CensoredDistributionを使って上限値と下限値の間で打ち切られた値の分布を，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使ってパレート分布を含むより高次元の分布を構築することが，ProductDistributionを使ってパレート分布を含む独立成分分布との結合分布を計算することができる．
  • ParetoDistributionは多くの他の分布と密接に関係している．例えば，パレート分布は，ZipfDistributionの連続版である．この定義の結果，パレート分布に従う確率変数の逆数はPowerDistributionに従う．さらに，パレート分布に従う確率変数の適切に中心が定まりスケールされた独立サンプルの値の合計の分布は，StableDistributionに近付くのに対し，ExponentialDistributionに従う確率変数の指数関数は ParetoDistributionに従う．ParetoDistributionは，LogNormalDistribution，BenktanderWeibullDistribution，BeniniDistribution，BenktanderGibratDistribution，ChiSquareDistribution，PearsonDistribution，BetaPrimeDistributionとも緊密に関係している．

例題

すべて開くすべて閉じる

例  (12)

タイプIのパレート分布の確率密度関数：

タイプIのパレート分布の累積分布関数：

タイプIのパレート分布の平均と分散：

タイプIのパレート分布の中央値：

タイプIIのパレート分布の確率密度関数：

タイプIIのパレート分布の累積分布関数：

タイプIIのパレート分布の平均と分散：

タイプIIのパレート分布の中央値：

タイプIVのパレート分布の確率密度関数：

タイプIVのパレート分布の累積分布関数：

タイプIVのパレート分布の平均と分散：

タイプIVのパレート分布の中央値：

スコープ  (10)

パレート分布から擬似乱数のサンプルを生成する：

そのヒストグラムを確率密度関数と比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：

タイプIのパレート分布とタイプIIのパレート分布の歪度は定義されているところでは α のみに依存する：

極限値：

タイプIVのパレート分布の歪度は位置母数 μ に依存しない：

タイプIのパレート分布とタイプIIのパレート分布の尖度は定義されているところでは等しい：

極限値：

タイプIVのパレート分布の尖度は位置母数 μ に依存しない：

母数の関数としての閉形式のタイプIのパレート分布の種々のモーメント：

Moment：

記号次数の閉形式：

CentralMoment：

記号次数の閉形式：

FactorialMoment：

Cumulant：

タイプIIのパレート分布の種々のモーメント：

Moment：

記号次数の閉形式：

CentralMoment：

FactorialMoment：

Cumulant：

タイプIVのパレート分布の種々のモーメント：

Moment：

CentralMoment：

FactorialMoment：

Cumulant：

タイプIのパレート分布のハザード関数：

タイプIIのパレート分布のハザード関数：

タイプIVのパレート分布のハザード関数：

タイプIのパレート分布の分位関数：

タイプIIのパレート分布の分位関数：

タイプIVのパレート分布の分位関数：

母数でQuantityを一貫して使うとQuantityDistributionが与えられる：

このモデルにおける給与の四分位数：

アプリケーション  (5)

裾部の長い分布としてのParetoDistributionは都市の人口サイズのモデル化に使うことができる：

人口サイズのヒストグラムを推定分布の確率密度関数と比較する：

ある都市の人口が少なくとも1万人である確率を求める：

平均的な都市のサイズを求める：

無作為に選んだ20都市の人口サイズのシミュレーションを行う：

ParetoDistributionを大規模な州立大学の収入のモデル化に使う：

パートタイムとフルタイムの給与を調整して非零の値を選ぶ：

パレート分布をデータにフィットする：

データのヒストグラムを推定分布の確率密度関数と比較する：

大規模な州立大学の平均給与を求める：

給与が最高で$50000になる確率を求める：

給与が最低でも$150000になる確率を求める：

給与の中央値を求める：

上記のような大学の無作為に選んだ100名の雇用者の給与のシミュレーションを行う：

あるデバイスの寿命はParetoDistributionに従う：

デバイスの信頼性を求める：

このデバイスの平均寿命を求める：

このデバイスが6年以上使用可能である確率を求める：

このデバイスの故障率を求める：

1935年から1989年までにアメリカ合衆国で記録された地震のマグニチュードについて考える：

リクタースケール(Richter scale)で記録されたマグニチュードの整数部分はParetoDistributionでモデル化できる：

マグニチュードのヒストグラムをフィットされた分布と比較する：

地震のマグニチュードがリクタースケールで最低でも6になる確率を求める：

マグニチュードの平均を求める：

次の30回の地震のシミュレーションを行う：

切断されたタイプIVのパレート分布を使ってBradford分布を定義する：

形状母数が0に近付く場合の密度関数の極限を求める：

定数を簡約するために代入する：

Bradford分布を定義する：

Bradford確率密度関数：

累積分布関数：

乱数を生成する：

特性と関係  (20)

パレート分布は平行移動の下では閉じている：

確率密度と確率変数にはベキ法則の関係がある：

パレート分布の族は最小値の下で閉じている：

形状母数の異なる値について：

切断の特殊ケース：

他の分布との関係：

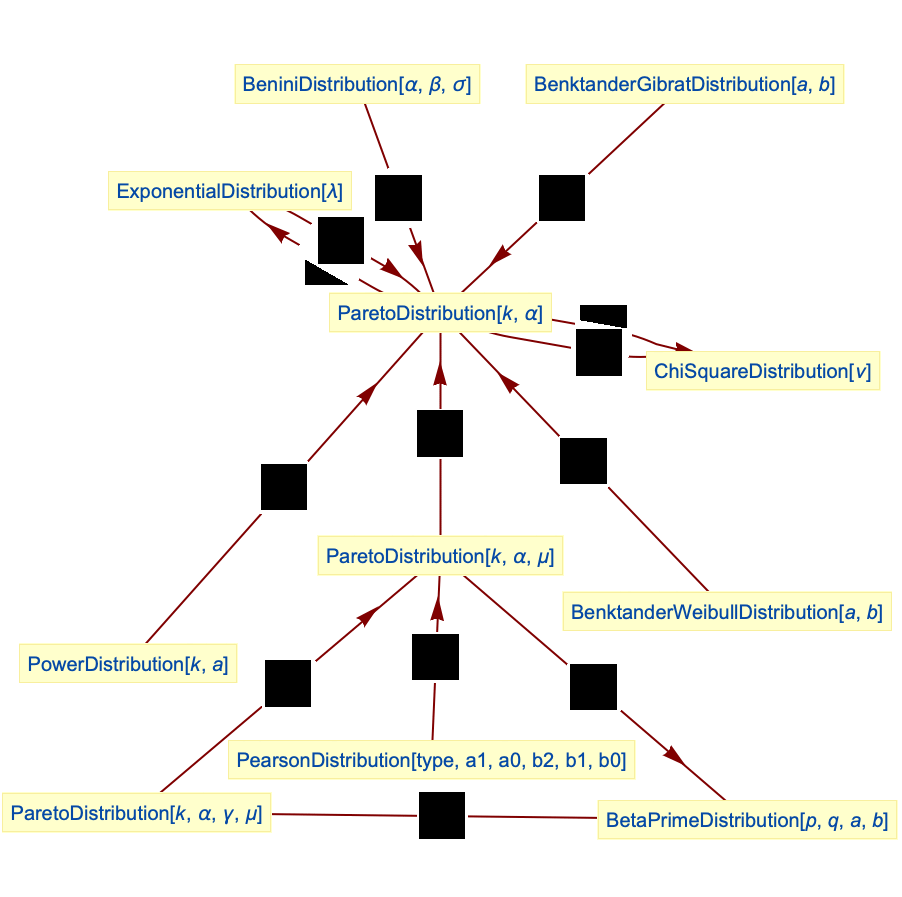
タイプIIのパレート分布はPearsonDistributionの特殊ケース（タイプVI）である：

タイプIのパレート分布はBeniniDistributionの特殊ケースである：

タイプIIのパレート分布は についてタイプIのパレート分布に簡約される：

タイプIVのパレート分布は についてタイプIIのパレート分布に簡約される：

パレート分布はPowerDistributionの逆の分布である：

パレート分布はBenktanderGibratDistributionの極限のケースである：

パレート分布はBenktanderWeibullDistributionの極限のケースである：

ChiSquareDistributionはパレート分布に従う変量を変換したものである：

ChiSquareDistributionはパレート分布に従う変量を変換したものである：

パレート分布はExponentialDistributionを変換したものである：

パレート分布を変換するとExponentialDistributionが得られる：

タイプIIのパレート分布はBetaPrimeDistributionに関連している：

タイプIVのパレート分布はBetaPrimeDistributionに関連している：

ParetoDistributionはExponentialDistributionとErlangDistributionの商として求めることができる：

ParetoDistributionはExponentialDistributionとGammaDistributionの商として求めることができる：

考えられる問題  (3)

ParetoDistributionは，k が実数でないときは定義されない：

ParetoDistributionは，α が正の実数でないときは定義されない：

記号出力に無効な母数値を代入すると意味のない結果が返される：

についてのタイプIIのパレート分布はタイプIのパレート分布ではない：

タイプIIのパレート分布は についてタイプIのパレート分布に簡約される：

おもしろい例題  (1)

累積分布関数の等高線を持つ γ のさまざまな値についての確率密度関数：

Wolfram Research (2007), ParetoDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/ParetoDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2007), ParetoDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/ParetoDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2007. "ParetoDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ParetoDistribution.html.

APA

Wolfram Language. (2007). ParetoDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ParetoDistribution.html

BibTeX

@misc{reference.wolfram_2024_paretodistribution, author="Wolfram Research", title="{ParetoDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ParetoDistribution.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_paretodistribution, organization={Wolfram Research}, title={ParetoDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/ParetoDistribution.html}, note=[Accessed: 22-November-2024 ]}