PearsonDistribution[a1,a0,b2,b1,b0]
母数が a1,a0,b2,b1,b0のピアソン(Pearson)の分布族を表す.
PearsonDistribution[type,a1,a0,b2,b1,b0]
指定された type のピアソン分布を表す.


PearsonDistribution
PearsonDistribution[a1,a0,b2,b1,b0]
母数が a1,a0,b2,b1,b0のピアソン(Pearson)の分布族を表す.
PearsonDistribution[type,a1,a0,b2,b1,b0]
指定された type のピアソン分布を表す.
詳細

- 確率密度
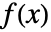 は微分方程式
は微分方程式 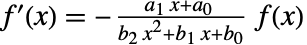 を満足する.
を満足する. - ピアソンの分布族は歴史的に7つのタイプに分類できる.PearsonDistribution[type,…]の形式が与えられると,各タイプは陰的に領域と母数の制約を与える.
- PearsonDistribution[1,…]はシフトされ再スケールされたBetaDistributionである.
- PearsonDistribution[2,…]は左右対称でシフトおよび再スケールされたBetaDistributionである.
- PearsonDistribution[3,…]はNormalDistributionとGammaDistributionを含む.
- PearsonDistribution[4,…]は標準分布には関係していない.
- PearsonDistribution[5,…]はシフトされたInverseGammaDistributionである.
- PearsonDistribution[6,…]はシフトおよび再スケールされたFRatioDistributionである.
- PearsonDistribution[7,…]はシフトおよび再スケールされたStudentTDistributionである.
- 記号母数でタイプの引数がない場合,母数の仮定が明示的には破られていない最初のタイプが仮定される.タイプは4,1,6,3,5,2,7の順で試される.
- 母数の仮定はDistributionParameterAssumptionsから得ることができる.
- PearsonDistributionでは,a1,a0,b2,b1,b0は,
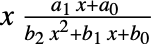 が無次元になるような x の単位を求められる数量でよい. »
が無次元になるような x の単位を求められる数量でよい. » - PearsonDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- PearsonDistributionは,引数の構造によって決定される,統計分布の7タイプのうちの1つに属するものを表す.ピアソン分布は,目に見えて歪んでいる分布をモデル化するためにこの分布を考案した,英国人の数学者であるカール・ピアソンに由来する.
- ピアソン分布の確率密度関数(PDF)の全体的な形は,その引数によって大きく変わる.例えば,タイプ1のピアソン分布のPDFは,単調増加,単調減少,1つの「峰」(つまり極大値)を持つのいずれかである.これに対し,タイプ4のピアソン分布のPDFは,常に単一の峰を持ち,歪んだ非対称ガウス分布と同じように見える.これに加え,さまざまなタイプのPearsonDistributionのPDFが,さまざまなタイプの区間上で定義されまたこれにサポートされる.(例えば,タイプ1のピアソン分布の領域は,有界で有限長であるのに対し,タイプ4の領域はのすべてである),そして,PDFの裾部は,タイプによって,「太い」(つまり,
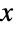 の大きい値について確率密度分布が非指数的に減少する)場合も,「薄い」(つまり,確率密度関数が大きい
の大きい値について確率密度分布が非指数的に減少する)場合も,「薄い」(つまり,確率密度関数が大きい 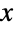 について指数的に減少する)場合もある.(この動作は,分布のSurvivalFunctionを解析することで,数量的に厳密にすることができる.)
について指数的に減少する)場合もある.(この動作は,分布のSurvivalFunctionを解析することで,数量的に厳密にすることができる.) - タイプ4のピアソン分布はデータあるいはモンテカルロシミュレーションから得られた分布をフィットするのによく使われるのに対し,その他のピアソン族は単峰型分布の近似を意図して使われる.これらの単峰型分布は,タイプ4によってうまくモデル化されるが,他のより「標準的な」分布によってはモデル化できない.多くの分布はピアソン分布族によって説明される(あるいは限定的な値および/または特殊ケースのピアソン族).つまり,ピアソン分布は,この分布がモデル化するような現象タイプについて非常に一般的なのである.例えば,ピアソン分布のある種のタイプは疫病伝播動作,ウィナー過程の特性,ベイズ統計学の基本概念,保険金支払い請求額の大きさ,細菌の遺伝子式の説明に基本的な役割を果たす.
- RandomVariateを使って,ピアソン分布からの1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,PearsonDistribution[type,a1,a0,b2,b1,b0]](より簡略すると xPearsonDistribution[type,a1,a0,b2,b1,b0])を使って,確率変数 x が指定されたタイプ type のピアソン分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 指定されたタイプ type のピアソン分布の確率密度関数および累積分布関数は,PDF[PearsonDistribution[type,a1,a0,b2,b1,b0],x]およびCDF[PearsonDistribution[type,a1,a0,b2,b1,b0],x]を使って得られることがある.ピアソン分布は,PDFが
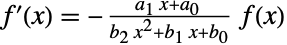 という形の単純な有理関数を含む1階の微分方程式を満足する点で特別である.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.ピアソン分布が有限の場合,最初の4つのモーメントがこれを一意的に決定する.
という形の単純な有理関数を含む1階の微分方程式を満足する点で特別である.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.ピアソン分布が有限の場合,最初の4つのモーメントがこれを一意的に決定する. - DistributionFitTestを使って,与えられたデータ集合がピアソン分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックピアソン分布を推定することが,FindDistributionParametersを使ってデータをピアソン分布にフィットすることができる.ProbabilityPlotを使って記号ピアソン分布の累積分布関数に対する与えられたデータの累積分布関数のプロットを生成することが,QuantilePlotを使って記号ピアソン分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたピアソン分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってピアソン分布を含む高次元分布を構築することが,ProductDistributionを使ってピアソン分布を含む独立成分分布の結合分布を計算することができる.
- PearsonDistributionは他の数多くの分布と関連している.例えば,タイプ1とタイプ2のピアソン分布は,シフトされ再スケールされたBetaDistributionであり,タイプ3のピアソン分布はNormalDistributionとGammaDistributionの両方を一般化し,タイプ5のピアソン分布はシフトされたInverseGammaDistributionであり,タイプ4とタイプ7のピアソン分布はそれぞれFRatioDistributionおよびStudentTDistributionのシフトされ再スケールされたバージョンである.タイプ4のピアソン分布は,このような一般的な意味では他の標準的な分布とは関連していないが,その確率密度分布はStudentTDistributionの非対称バージョンのように見える.さらに,引数の値によっては,タイプ4のピアソン分布はCauchyDistributionの一般化になる.PearsonDistributionは,ArcSinDistribution,BetaPrimeDistribution,PowerDistribution,ParetoDistribution,LevyDistribution,InverseChiSquareDistribution,HotellingTSquareDistribution,HalfNormalDistribution,ErlangDistributionとも密接な関係がある.
例題
すべて開く すべて閉じるスコープ (8)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
ピアソン分布(タイプ4)の母数の関数としての閉じた形の種々のモーメント:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (3)
タイプ4のPearsonDistributionは他の標準分布と関連がない唯一のタイプである:
タイプ4のピアソン分布の確率変量がプロットされた範囲の外にある確率を求める:
PearsonDistributionのモーメントは定義微分方程式で密度関数 ![]() について暗示された三項再帰方程式を満足する:
について暗示された三項再帰方程式を満足する:
ゼロ平均と単位分散を持ち歪度と尖度でパラメータ化されたピアソン分布を定義する:
モーメントがサンプリングモーメントにマッチするPearsonDistributionのタイプを判断する:
特性と関係 (24)
PearsonDistribution族のあるものはアフィン変換下では閉じた形になる:
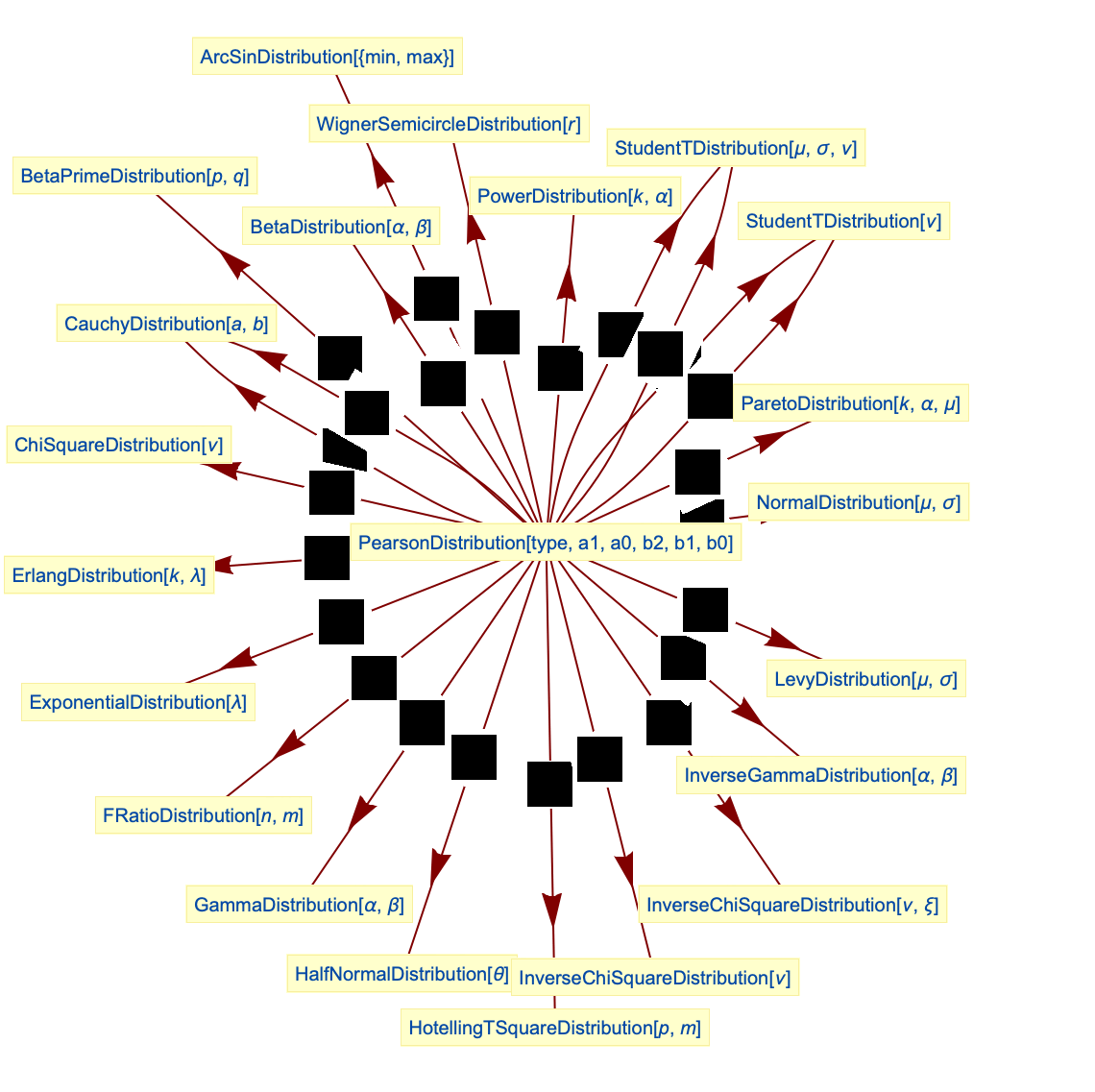
ArcSinDistributionはタイプ1とタイプ2のピアソン分布の特殊ケースである:
BetaDistributionはタイプ1のピアソン分布の特殊ケースである:
PowerDistributionはタイプ1のピアソン分布の特殊ケースである:
WignerSemicircleDistributionはタイプ1とタイプ2のピアソン分布の特殊ケースである:
ChiSquareDistributionはタイプ3のピアソン分布の特殊ケースである:
ErlangDistributionはタイプ3のピアソン分布の特殊ケースである:
ExponentialDistributionはタイプ3のピアソン分布の特殊ケースである:
GammaDistributionはタイプ3のピアソン分布の特殊ケースである:
スケールされたHalfNormalDistributionはタイプ3のピアソン分布の特殊ケースである:
NormalDistributionはタイプ3のピアソン分布の特殊ケースである:
CauchyDistributionはタイプ4のピアソン分布の極限のケースである:
CauchyDistributionはタイプ7のピアソン分布の特殊ケースである:
StudentTDistributionはタイプ4とタイプ7のピアソン分布の特殊ケースである:
一般化されたStudentTDistributionはタイプ4とタイプ7のピアソン分布の特殊ケースである:
InverseChiSquareDistributionはタイプ5のピアソン分布の特殊ケースである:
スケールされたInverseChiSquareDistributionはタイプ5のピアソン分布の特殊ケースである:
InverseGammaDistributionはタイプ5のピアソン分布の特殊ケースである:
LevyDistributionはタイプ5のピアソン分布の特殊ケースである:
BetaPrimeDistributionはタイプ6のピアソン分布の特殊ケースである:
FRatioDistributionはタイプ6のピアソン分布の特殊ケースである:
HotellingTSquareDistributionはタイプ6のピアソン分布の特殊ケースである:
ParetoDistributionはタイプ6のピアソン分布の特殊ケースである:
関連するガイド
テキスト
Wolfram Research (2010), PearsonDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/PearsonDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "PearsonDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/PearsonDistribution.html.
APA
Wolfram Language. (2010). PearsonDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PearsonDistribution.html
BibTeX
@misc{reference.wolfram_2025_pearsondistribution, author="Wolfram Research", title="{PearsonDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/PearsonDistribution.html}", note=[Accessed: 22-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_pearsondistribution, organization={Wolfram Research}, title={PearsonDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/PearsonDistribution.html}, note=[Accessed: 22-February-2026]}