StationaryWaveletPacketTransform

StationaryWaveletPacketTransform[data]

data 配列の定常ウェーブレットパケット変換(SWPT)を与える．

StationaryWaveletPacketTransform[data,wave]

ウェーブレット wave を使った定常ウェーブレットパケット変換を与える．

StationaryWaveletPacketTransform[data,wave,r]

r 個の細分化レベルを使う定常ウェーブレットパケット変換を与える．

詳細とオプション

  • StationaryWaveletPacketTransformは，ウェーブレット係数の完全木が計算されるStationaryWaveletTransformを一般化したものである．
  • StationaryWaveletPacketTransformはDiscreteWaveletDataオブジェクトを与える．
  • DiscreteWaveletData dwd の特性は dwd["prop"]で得られる．使用可能な特性のリストは dwd["Properties"]で得られる．
  • 結果のウェーブレット係数は入力 data と同じ深さ，同じ次元の配列である．
  • data は次のいずれでもよい．
  • list任意階数の数値配列
    image任意のImageオブジェクト
    audioAudioオブジェクトまたはサンプルされたSoundオブジェクト
  • 使用可能なウェーブレット wave
  • BattleLemarieWavelet[…]Bスプラインに基づいたBattle–Lemariéウェーブレット
    BiorthogonalSplineWavelet[…]Bスプラインに基づいたウェーブレット
    CoifletWavelet[…]Daubechiesウェーブレットの対称性変種
    DaubechiesWavelet[…]Daubechiesウェーブレット
    HaarWavelet[…]古典的なHaarウェーブレット
    MeyerWavelet[…]周波数領域で定義されるウェーブレット
    ReverseBiorthogonalSplineWavelet[…]Bスプラインに基づいたウェーブレット（逆双対ウェーブレットと主ウェーブレット）
    ShannonWavelet[…]シンク関数に基づいたウェーブレット
    SymletWavelet[…]最小非対称直交ウェーブレット
  • デフォルト wave はHaarWavelet[]である．
  • 細分化レベル r の設定値を高くすると，スケールの大きい特徴が解決される．
  • デフォルトの細分化レベル r はmin(TemplateBox[{{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, n, )}, +, {1, /, 2}}}, Floor],4)で与えられる．ただし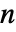， は data の最小次元である．
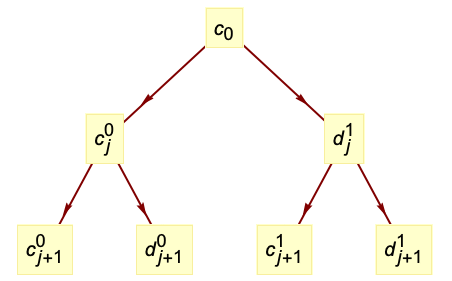
  • 細分化レベルがFullのとき，r はTemplateBox[{{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, n, )}, +, {1, /, 2}}}, Floor]で与えられる．
  • レベル 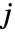のウェーブレット係数の木は，粗い係数 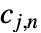と詳細化係数 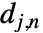からなる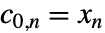． は入力 data を表す．
  • 前方変換は 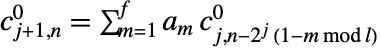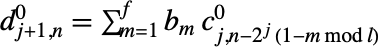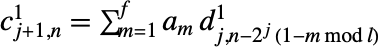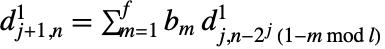，，，で与えられる．ただし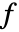， は対応する wspec のフィルタ長であり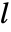， は入力 data の長さである．
  • 逆変換は 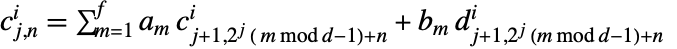で与えられる．
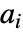  • はローパスフィルタ係数で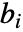， はハイパスフィルタ係数である．どちらもそれぞれのウェーブレット族で定義される．
  • 使用可能なオプション
  • MethodAutomatic使用するメソッド
    WorkingPrecision MachinePrecision内部計算で使用する精度
  • StationaryWaveletPacketTransformはデータに対して周期的充填を行う．
  • InverseWaveletTransformは逆変換を与える．
  • デフォルトで，InverseWaveletTransformは再構成の際に dwd["BasisIndex"]で表される係数を使う．また，WaveletBestBasisを使って計算や最適な底の設定を行う．

例題

すべて開くすべて閉じる

例  (3)

定常ウェーブレットパケット変換を計算する：

結果のDiscreteWaveletDataはウェーブレット係数の完全木を表す：

逆変換で入力が再構築される：

音声信号を変換する：

dwd[…,"Audio"]を使って係数信号を取り出す：

逆変換を計算する：

Imageオブジェクトを変換する：

dwd[…,"Image"]を使って係数画像を抽出する：

逆変換を計算する：

スコープ  (33)

基本的な用法  (4)

DiscreteWaveletDataオブジェクトから有益な特性を抽出することができる：

特性の完全リストを得る：

データと係数の次数を得る：

Normalを使ってすべてのウェーブレット係数を明示的に得る：

Allを引数として使ってすべての係数を得ることもできる：

Automaticを使って逆変換で使われる係数だけを得る：

"TreeView"または"WaveletIndex"を使ってどのウェーブレット係数が使えるかを調べる：

特定の係数配列を抽出する：

ウェーブレット指標指定のリストに対応するいくつかのウェーブレット係数を抽出する：

ウェーブレット指標がパターンにマッチするすべての係数を抽出する：

より高い細分化レベルを使って周波数分解能を高くする：

細分化レベルが低いと，より多くの信号エネルギーが{0,0}に残される：

さらに細分化を進めると，{0,0}はより一層要素に分解される：

ウェーブレット族  (10)

異なるウェーブレット族を使ってウェーブレットパケット変換を計算する：

係数を比較する：

異なるウェーブレット族を使って異なる特徴を捉える：

HaarWavelet（デフォルト）：

DaubechiesWavelet：

BattleLemarieWavelet：

BiorthogonalSplineWavelet：

CoifletWavelet：

MeyerWavelet：

ReverseBiorthogonalSplineWavelet：

ShannonWavelet：

SymletWavelet：

一次元データ  (6)

WaveletListPlotを使って係数を共通水平軸上にプロットする：

共通垂直軸に対してプロットする：

WaveletScalogramを使い，係数を時間と細分化レベルの関数として可視化する：

マウスポインタが係数上に置かれると係数指標がツールチップとして現れる：

定数データ：

粗い係数{0,0,…}を除き，すべての係数が小さい：

分解可能な最高の周波数（ナイキスト(Nyquist)周波数）で振動するデータ：

小さくないのは第1詳細化係数{1}とその粗い子係数{1,0,0,…}のみである：

大きい不連続箇所のあるデータ：

粗い係数{0,…}はデータと同じ大きいスケールの構造を持つ：

詳細化係数は不連続箇所に敏感である：

空間構造と周波数構造の両方を持つデータ：

粗い係数{0,…}はデータの局所平均を辿る：

第1詳細化係数{1}とその粗い子係数{1,0,…}は振動を表す：

共通垂直軸上のすべての係数：

二次元データ  (5)

二次元定常ウェーブレットパケット変換を計算する：

ウェーブレット係数の木構造を見る：

逆変換をするともとの信号に戻る：

dwd[…,"MatrixPlot"]を使い，各係数をMatrixPlotで可視化する：

対角詳細化係数{3}とその子係数{3,__}を可視化する：

二次元では，各方向のフィルタリング操作のベクトルが計算できる：

これらのベクトルを二進数展開として解釈するとウェーブレット指標の数が得られる：

Haarウェーブレットのローパスフィルタとハイパスフィルタを得る：

結果の2Dフィルタは2方向のフィルタの外積である：

ステップデータのウェーブレット変換：

垂直方向に不連続性を有するデータ：

すべての水平および対角詳細化係数，つまりウェーブレット指標{___,2|3,___}は0である：

水平に不連続性を有するデータ：

すべての垂直および対角詳細化係数，つまりウェーブレット指標{___,1|3,___}は0である：

より高次元のデータ  (2)

三次元ウェーブレットパケット変換を計算する：

計算されたすべてのウェーブレット係数をリストにする：

逆変換でもとの信号に戻る：

三次元クロス配列のウェーブレット変換：

ローパスウェーブレット係数{___,0}を可視化する：

もとのデータのエネルギーは変換された係数内に保存されている：

音声データ  (2)

Audioオブジェクトを変換する：

逆変換すると再構築された音声が返される：

デフォルトで，係数は各サウンドチャンネル用のデータのリストとして与えられる：

{1,1}係数をAudioオブジェクトとして取得する：

{1,1}係数のAudioオブジェクトとしての逆変換：

サウンドデータ  (2)

Soundオブジェクトを変換する：

逆変換すると再構築された音声オブジェクトが与えられる：

MenuViewを使ってすべての係数をブラウズする：

画像データ  (2)

Imageオブジェクトを変換する：

逆変換するとImageオブジェクトが再構築される：

ウェーブレット係数は通常各画像チャンネルのデータのリストとして与えられる：

代りに，すべての係数をImageオブジェクトとして得る：

カラーレベルの再スケールを施していない生のImageオブジェクトを得る：

{0,1}係数の逆変換をImageオブジェクトとして得る：

一般化と拡張  (3)

StationaryWaveletPacketTransformは記号による量の配列に使うことができる：

逆変換で入力が厳密に復元される：

任意の内部作業精度を指定する：

複素数値のデータを使う：

ウェーブレット係数が複素数になる：

オプション  (3)

WorkingPrecision  (3)

デフォルトで，WorkingPrecision->MachinePrecisionが使われる：

より精度の高い評価を使う：

WorkingPrecision->∞を使って厳密計算を行う：

特性と関係  (10)

StationaryWaveletPacketTransformはウェーブレット係数の完全木を計算する：

StationaryWaveletTransformは係数の完全木の部分木を計算する：

DiscreteWaveletPacketTransform係数は細分化の各レベルで長さが半分になる：

循環されたデータは異なる係数を与える：

StationaryWaveletPacketTransform係数はデータと同じ長さである：

循環されたデータは循環された係数を与える：

デフォルトの細分化はMin[Round[Log2[Min[Dimensions[data]]]],4]で与えられる：

より高次元：

直交ウェーブレット族用のエネルギーのノルムは保存される：

双直交ウェーブレット族用のエネルギーのノルムはほぼ保存される：

データの平均は変換の最高細分化レベルで捉えられる：

最高細分化レベルの係数を抽出する：

個々の係数配列からの逆変換の総和はもとのデータを与える：

各ウェーブレット係数配列を別々に逆変換させる：

その総和でもとのデータが与えられる：

一次元のHaar定常ウェーブレットパケット変換を計算する：

{0}と{1}のウェーブレット係数を計算する：

StationaryWaveletPacketTransformで計算する：

二次元では，各次元で異なるフィルタが適用される：

Haarウェーブレットのローパスとハイパスのフィルタ：

行列データのHaarウェーブレット変換：

HaarWaveletを使ってStationaryWaveletPacketTransformと比較する：

画像チャンネルは別々に変換される：

別々に変換された画像チャンネルの{0}係数を組み合せる：

もと画像のStationaryWaveletPacketTransformの{0}係数と比較する：

画像は同じである：

Wolfram Research (2010), StationaryWaveletPacketTransform, Wolfram言語関数， https://reference.wolfram.com/language/ref/StationaryWaveletPacketTransform.html （2017年に更新）.

テキスト

Wolfram Research (2010), StationaryWaveletPacketTransform, Wolfram言語関数， https://reference.wolfram.com/language/ref/StationaryWaveletPacketTransform.html （2017年に更新）.

CMS

Wolfram Language. 2010. "StationaryWaveletPacketTransform." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/StationaryWaveletPacketTransform.html.

APA

Wolfram Language. (2010). StationaryWaveletPacketTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StationaryWaveletPacketTransform.html

BibTeX

@misc{reference.wolfram_2024_stationarywaveletpackettransform, author="Wolfram Research", title="{StationaryWaveletPacketTransform}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/StationaryWaveletPacketTransform.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_stationarywaveletpackettransform, organization={Wolfram Research}, title={StationaryWaveletPacketTransform}, year={2017}, url={https://reference.wolfram.com/language/ref/StationaryWaveletPacketTransform.html}, note=[Accessed: 22-November-2024 ]}