StationaryWaveletTransform
StationaryWaveletTransform[data]
data の配列の定常ウェーブレット変換(SWT)を与える.
StationaryWaveletTransform[data,wave]
ウェーブレット wave を使って定常ウェーブレット変換を与える.
StationaryWaveletTransform[data,wave,r]
レベル r の細分化を使って定常ウェーブレット変換を与える.
詳細とオプション



- StationaryWaveletTransformはDiscreteWaveletTransformに似ているが,どの細分化レベルにおいてもサブサンプリングが起こらず,結果の係数配列がすべてもとのデータと同次元である点が異なる.
- StationaryWaveletTransformはDiscreteWaveletDataオブジェクトを与える.
- DiscreteWaveletData dwd の特性は dwd["prop"]で求まり,使用可能な特性のリストは dwd["Properties"]で得られる.
- data は次のいずれでもよい.
-
list 任意階数の数値配列 image 任意のImageオブジェクト audio AudioオブジェクトまたはサンプルされたSoundオブジェクト - 使用可能なウェーブレット wave
-
BattleLemarieWavelet[…] Bスプラインに基づいたBattle–Lemariéウェーブレット BiorthogonalSplineWavelet[…] Bスプラインに基づいたウェーブレット CoifletWavelet[…] Daubechiesウェーブレットの対称性変種 DaubechiesWavelet[…] Daubechiesウェーブレット HaarWavelet[…] 古典的なHaarウェーブレット MeyerWavelet[…] 周波数領域で定義されたウェーブレット ReverseBiorthogonalSplineWavelet[…] Bスプラインに基づいたウェーブレット(逆双対ウェーブレットと主ウェーブレット) ShannonWavelet[…] シンク関数に基づいたウェーブレット SymletWavelet[…] 最小非対称直交ウェーブレット - デフォルトの wave はHaarWavelet[]である.
- 細分化レベル r を最高にすると,スケールの大きい特徴が解決される.
- デフォルトの細分化レベル r は
![TemplateBox[{{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, n, )}, +, {1, /, 2}}}, Floor] TemplateBox[{{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, n, )}, +, {1, /, 2}}}, Floor]](Files/StationaryWaveletTransform.ja/1.png) で与えられる.ただし,
で与えられる.ただし,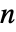 は data の最小次元である. »
は data の最小次元である. » - レベル
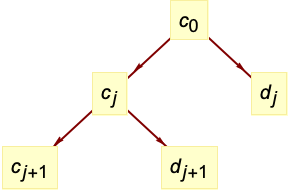
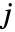 におけるウェーブレット係数の木は粗い係数
におけるウェーブレット係数の木は粗い係数 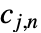 と詳細化係数
と詳細化係数 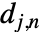 からなる.
からなる.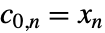 は入力 data を表す.
は入力 data を表す. - 前方変換は
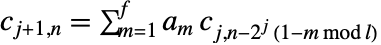 と
と 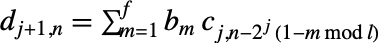 で与えられる.ただし,
で与えられる.ただし,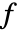 は対応する wspec のフィルタの長さであり,
は対応する wspec のフィルタの長さであり,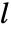 は入力 data の長さである. »
は入力 data の長さである. » - 逆変換は
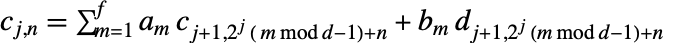 で与えられる. »
で与えられる. » 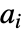 はローパスフィルタ係数で,
はローパスフィルタ係数で,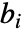 はハイパスフィルタ係数である.どちらも各ウェーブレット族で定義される.
はハイパスフィルタ係数である.どちらも各ウェーブレット族で定義される.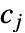 と
と 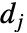 の次元は入力 data の次元に等しい.
の次元は入力 data の次元に等しい.- 使用可能なオプション
-
Method Automatic 使用するメソッド WorkingPrecision MachinePrecision 内部計算で使用する精度 - StationaryWaveletTransformはデータを周期的に充填する.
- InverseWaveletTransformは逆変換を与える.
例題
すべて開くすべて閉じる例 (3)
スコープ (34)
基本的な用法 (6)
結果のDiscreteWaveletDataは変換係数の木構造を表している:
DiscreteWaveletDataオブジェクトから有用な特性を抽出することができる:
Normalを使ってウェーブレットのすべての係数を明示的に求める:
Allを引数として使ってすべての係数を得ることもできる:
Automaticを使って逆変換に使われた係数だけを求める:
"TreeView"または"IndexMap"を使ってどのウェーブレット係数が使えるかを明らかにする:
ウェーブレットの指標指定リストに対応するいくつかのウェーブレット係数を抽出する:
ウェーブレット指標がパターンにマッチするすべての係数を抽出する:
WaveletListPlot等の関数では,デフォルトでAutomatic係数が使われている:
ウェーブレット族 (10)
ベクトルデータ (6)
WaveletListPlotを使って,係数を共通水平軸上でプロットする:
WaveletScalogram使い,係数を時間と細分化レベルの関数として可視化する:
マウスポインタが係数上にくると,係数指標がツールチップとして現れる:
分解可能な最高の周波数(ナイキスト(Nyquist)周波数)で振動するデータ:
行列データ (5)
dwd[…,"MatrixPlot"]を使って各係数をMatrixPlotとして可視化する:
二次元では,各方向のフィルタリング操作のベクトルが計算できる:
これらのベクトルを二進数展開として解釈するとウェーブレット指標の数が得られる:
Haarウェーブレットのローパスフィルタとハイパスフィルタを得る:
配列データ (2)
画像データ (2)
一般化と拡張 (3)
StationaryWaveletTransformは記号による量の配列に使うことができる:
オプション (3)
WorkingPrecision (3)
アプリケーション (3)
逆網点化 (1)
GaussianFilterを詳細化係数に適用する:
数値微分 (1)
平行移動回転変換(TRT, Translation-Rotation-Transform)は線形要素を入力信号から取り除くことで境界効果を少なくするために使われる:
HaarWaveletには消失モーメントがあるので,![]() のウェーブレット変換を行うためにこれを選ぶ:
のウェーブレット変換を行うためにこれを選ぶ:
詳細化係数がデータの微分を与える.ノイズを最小にするために細分化レベル4の係数が選ばれる:
画像融合 (1)」
組合わさったウェーブレット係数の新たなDiscreteWaveletDataを構築する:
特性と関係 (12)
StationaryWaveletPacketTransformウェーブレット係数の完全木を計算する:
StationaryWaveletTransformは係数の完全木の部分木を計算する:
DiscreteWaveletTransform係数は細分化の各レベルで長さが半分になる:
StationaryWaveletTransform係数はもとのデータと同じ長さである:
エネルギーのノルムは双直交ウェーブレット族用に近似的に保存される:
DiscreteWaveletPacketTransformと比較する:
HaarWaveletを使ってDiscreteWaveletPacketTransformと比較する:
もと画像のStationaryWaveletTransformの{0}係数と比較する:
テキスト
Wolfram Research (2010), StationaryWaveletTransform, Wolfram言語関数, https://reference.wolfram.com/language/ref/StationaryWaveletTransform.html (2017年に更新).
CMS
Wolfram Language. 2010. "StationaryWaveletTransform." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/StationaryWaveletTransform.html.
APA
Wolfram Language. (2010). StationaryWaveletTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StationaryWaveletTransform.html