StationaryWaveletTransform
StationaryWaveletTransform[data]
给出由 data 组成的数组的平稳小波变换(SWT).
StationaryWaveletTransform[data,wave]
给出使用 wave 的平稳小波变换.
StationaryWaveletTransform[data,wave,r]
给出使用 r 级细化得到的平稳小波变换.
更多信息和选项



- StationaryWaveletTransform 与 DiscreteWaveletTransform 类似,除了在任何细化级别都不进行子采样,并且所得的系数数组都具有与原始数据相同的维数.
- StationaryWaveletTransform 给出一个 DiscreteWaveletData 对象.
- DiscreteWaveletData dwd 的属性可以使用 dwd["prop"] 找到,并且可用属性的列表可以使用dwd["Properties"] 找到.
- data 可以为以下形式:
-
list 任意阶数的数值数组 image 任意 Image 对象 audio Audio 或采样 Sound 对象 - 可能的小波 wave 包括:
-
BattleLemarieWavelet[…] 基于 B 样条的 Battle‐Lemarié 小波 BiorthogonalSplineWavelet[…] 基于 B 样条的小波 CoifletWavelet[…] Daubechies 小波的对称变种 DaubechiesWavelet[…] Daubechies 小波 HaarWavelet[…] 经典的 Haar 小波 MeyerWavelet[…] 在频域定义的小波 ReverseBiorthogonalSplineWavelet[…] 基于 B 样条的小波(反向原始-对偶) ShannonWavelet[…] 基于 sinc 函数的小波 SymletWavelet[…] 最小不对称正交小波 - 默认的 wave 是 HaarWavelet[].
- 在精细度 r 的较高设置下,解决了大规模的特点.
- 默认精细度 r 由
![TemplateBox[{{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, n, )}, +, {1, /, 2}}}, Floor] TemplateBox[{{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, n, )}, +, {1, /, 2}}}, Floor]](Files/StationaryWaveletTransform.zh/1.png) 给出,其中
给出,其中 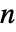 是 data 的最小维度. »
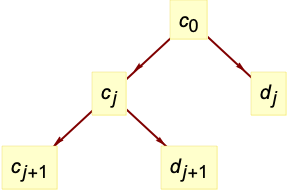
是 data 的最小维度. » - 小波系数组成的树在第
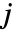 层包括粗系数
层包括粗系数 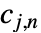 和细系数
和细系数 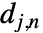 ,其中
,其中 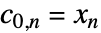 表示输入 data.
表示输入 data. - 正向变换由
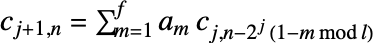 和
和 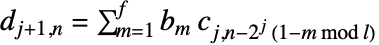 给出,其中
给出,其中 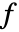 是对应的 wspec 的滤波器长度,而
是对应的 wspec 的滤波器长度,而 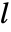 是输入 data 的长度. »
是输入 data 的长度. » - 逆变换由
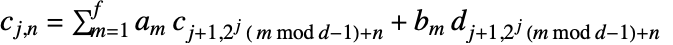 给出. »
给出. » 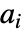 是低通滤波器系数,而
是低通滤波器系数,而 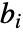 是为每个小波群定义的高通滤波器系数.
是为每个小波群定义的高通滤波器系数. 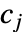 和
和 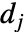 的维度与输入 data 的维度相同.
的维度与输入 data 的维度相同.- 可以给出如下选项:
-
Method Automatic 所要使用的方法 WorkingPrecision MachinePrecision 在内部计算中所要使用的精度 - StationaryWaveletTransform 使用数据的周期性填充 (periodic padding).
- InverseWaveletTransform 给出逆变换.
范例
打开所有单元关闭所有单元基本范例 (3)
范围 (34)
基本用途 (6)
所得的 DiscreteWaveletData 表示一个由变换系数组成的树:
可以从 DiscreteWaveletData 对象提取有用的属性:
使用 Normal 以明确获取所有小波系数:
也使用 All 作为一个变量以获取所有系数:
使用 Automatic 仅获取在逆变换中所用的系数:
使用 "TreeView" 或者 "IndexMap" 来找到可用的小波系数:
默认情况下,Automatic 系数在函数如 WaveletListPlot 中使用:
小波群 (10)
向量数据 (6)
使用 WaveletListPlot 在一个共用水平轴上绘制系数:
使用 WaveletScalogram,将系数可视化为以时间和精细度为变量的函数:
矩阵数据 (5)
使用 dwd[…,"MatrixPlot"] 将每个系数可视化为一个 MatrixPlot:
图像数据 (2)
推广和延伸 (3)
StationaryWaveletTransform 对符号形式的数量组成的数组起作用:
选项 (3)
WorkingPrecision (3)
应用 (3)
逆半调 (1)
在细系数上应用 GaussianFilter :
数值微分 (1)
通过从输入信号减去线性成分使用翻译-旋转-变换(Translation-Rotation-Transform (TRT) )减少边界效应:
因为 HaarWavelet 有一个消失矩,选择它来进行在 ![]() 上的小波变换:
上的小波变换:
图像融合 (1)
属性和关系 (12)
StationaryWaveletPacketTransform 计算由小波系数组成的完全树:
StationaryWaveletTransform 计算系数组成的完全树的一个子集:
DiscreteWaveletTransform 系数在每个精细度长度缩短一半:
StationaryWaveletTransform 系数具有和原始数据相同的长度:
与 DiscreteWaveletPacketTransform 比较:
使用 HaarWavelet 与 DiscreteWaveletPacketTransform 比较:
与原始图像的 StationaryWaveletTransform 的 {0} 系数比较:
文本
Wolfram Research (2010),StationaryWaveletTransform,Wolfram 语言函数,https://reference.wolfram.com/language/ref/StationaryWaveletTransform.html (更新于 2017 年).
CMS
Wolfram 语言. 2010. "StationaryWaveletTransform." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2017. https://reference.wolfram.com/language/ref/StationaryWaveletTransform.html.
APA
Wolfram 语言. (2010). StationaryWaveletTransform. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/StationaryWaveletTransform.html 年