数

数の型任意精度の計算
複素数任意精度の数
数と数値機械精度の数値
数の桁区間演算
厳密値と近似値不定形・無限大
数値の精度数値計算の抑制
数の型
Wolframシステムには，4つの数の型が組み込まれている．
Integer
任意の桁数の整数
Rational
integer/integer の約分された分数
Real
指定された桁精度で近似された実数
Complex
number+number Iの形の複素数
Wolframシステム内部での数の型
有理数は，常に約分された整数の比として表される：
小数点を用いると，整数や有理数ではなく，実数の近似値として扱われる：
近似値としての実数の桁数は何であってもよい：
複素数は整数や有理数の成分で構成してもよい：
実数を成分としてもよい：
123
整数
123.
実数の近似値
123.0000000000000
指定された桁精度を持つ近似値
123.+0.I
実数の近似値を成分とする複素数（実部と虚部が近似値）
型の違いによる値123の意味の相違
Wolframシステムでは，頭部（ヘッド）を調べることによって数の型の区別を確認することができる．（他の表記物と同様に数も頭部を持つが，数の頭部は型以外の情報を持たない．）
値123は，頭部Integerを持つ厳密な整数である：
今度は小数点を指定し，値123.を実数として入力する．型を確認すると頭部Realを持つ実数型が返される：
NumberQ[x]
x が数かどうか判定する
IntegerQ[x]
x が整数かどうか判定する
EvenQ[x]
x が偶数かどうか判定する
OddQ[x]
x が奇数かどうか判定する
PrimeQ[x]
x が素数かどうか判定する
Head[x]===type
数の型を判定する
数の型の判定関数
NumberQ[x]は，どんな型の数に対しても判定を行う：
5.は実数(Real)の近似値として扱われるのでIntegerQはFalseを返す：
複素数をよく使う場合，虚数部の表記によっては微妙な違いが生じるので気を付ける必要がある．入力値123.は実数として扱われ，その虚数部分は厳密なゼロとされる．しかし，虚数部がある精度のもとで近似値としてゼロとなっているような複素数を扱いたいという場合もあるだろう．
虚数部分を厳密な整数0とすると，複素数は実数に簡約される：
ここで，虚数部は特定の精度までのゼロなので，複素数のまま保持される：
複素数の虚数部が厳密なゼロか有限精度のゼロかどうかを区別することは理屈っぽいだけで実用的な意味がないように思われる．しかし，区別することは重要で，「一意的な値を持たない関数」で説明するが，複素数を使ったベキと根の解釈でこの違いは大きな意味を持つ．
数の型を調べるにはHead[expr]を使えば，Wolframシステムが保持する数の頭部が参照できる．しかし，多くの場合はIntegerQのような関数で特定の型かどうかを調べる方が手っ取り早い．これらの判定関数は引数が調べる型に属するときTrueを返し，そうでなければFalseを返す．例えば，判定する前に整数の型をxに割り当てておかなければ，IntegerQ[x]はFalseを返してくる．
複素数
複素数を入力するにはを意味する定数Iを使う．Iは大文字であることに注意する．
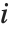ノートブックを使っているなら，ユーザはEsciiEscとタイプすることによってIを のように入力することができる（「ノートブックにおける数学表記法」参照）．出力には記号 が通常は使われる．通常のiは単に という変数を表し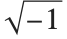，を意味しないことに注意しよう．
虚数 が求まる：
2つの複素数の比を計算させる：
複素数の指数関数を数値近似させる：
x+I y
複素数
Re[z]
実数部分
Im[z]
虚数部分
Conjugate[z]
共役複素数 または
Abs[z]
絶対値
Arg[z]
偏角 （ただし）
複素数の表記法と関連関数
数と数値
NumberQ[expr]
式 expr が数かどうかを判定する
NumericQ[expr]
式 expr が数値的な量を持つかどうかを判定する
数の型と数値の型の判定
Piは代数記号であるから，Pi+3は明確な数ではない：
しかし，特定の数値は持っている：
Pi+3がどんな値か確認してみる：
Wolfram言語は，Pi等の定数は記号であって数ではないが，特定の数値を持っていることを認識する．同じように，LogやSin等の標準的な関数についても変数の値が数値となっているときには関数の値も数値と認識する．
Log[2+x]は未知数xを含むため，数値ではない：
多くの関数は数値を持つ引数を前提にしている：
属性NumericFunctionを持つ関数は，一般に，引数が数値的なものである限り何らかの数値を返す．標準的なWolfram言語の関数はすべてこの属性を持っている．ユーザ定義の関数に関してはその限りではない．特別にWolfram言語に指示し，引数を数値として扱いたければユーザ定義の関数にこの属性を特別に与える必要がある．
数の桁
IntegerDigits[n]
整数 n の10進法表記の各桁をリストアップする
IntegerDigits[n,b]
n の b 進法表記の各桁をリストアップする
IntegerDigits[n,b,len]
合計桁数が len になるように左側を0で充填した桁をリストアップする
IntegerLength[n]
n の10進法表記の桁数
IntegerLength[n,b]
n の b 進法表記の桁数
IntegerExponent[n,b]
n の b 進法表記の最後に付く0の個数
RealDigits[x]
近似実数 x の10進法表記の各桁をリストアップし，小数点以上の桁数も表示する
RealDigits[x,b]
x の b 進法表記の各桁をリストアップする
RealDigits[x,b,len]
x の b 進法表記の右端の桁から数え len 桁目までの桁をリストアップする
RealDigits[x,b,len,n]
bn の係数で指定される桁から数えて len 桁目までの桁をリストアップする
FromDigits[list]
10進値の数の列を桁成分とする数を生成する
FromDigits[list,b]
b 進法の数の列を桁成分とする数を生成する
FromDigits["string"]
数列から整数を生成する
FromDigits["string",b]
b 進法の数列から整数を生成する
IntegerString[n]
整数 n 中の10進法の数列
IntegerString[n,b]
b 進法における n の桁数字の数列
数からリストあるいは桁成分への変換と逆変換
整数の各桁を16進法表記でリストアップする：
各桁の数のリストと小数点以上の桁数を出力する：
56を2進法表記で桁をリストアップし，リスト長が8になるようにリストの左側にゼロを足し加える：
2進値リストからもとの数を再生する：
これは56を2進法で表したものである：
もとの数を再生する：
b^^nnnn
b 進法表記の数
BaseForm[x,b]
数 x を b 進法表記で表示する
IntegerString[n,b]
数 n を b 進法表記で表す文字列
10進法以外の表記指定と表示
10進法以上を使う場合，各桁に現れる数が10以上の値を持つときはa–zのアルファベットで表される．
2進数は10進法表記でになる：
値を2進数で出力する：
以下は，2進法表記を文字列として与える：
16進数を10進法表記にする：
16進数の計算もできる．この例では答が10進法で出力される：
答を16進数に変換する：
この例のように，整数だけでなく実数近似値も10進法以外の表記法で表すことができる：
を特別な桁精度で近似し，結果を8進法表記で出力する：
左端桁から数え15桁目までの桁成分を8進法表記でリストアップする：
の桁から数えて15桁の要素をリストアップする：
「数値の出力書式」において数を表示するために使う各種書式を説明している．特別な書式を使う場合，関数MantissaExponentを使い実数の構成成分をあらかじめ分解しておく必要がある．
MantissaExponent[x]
x を仮数部と指数部に分離しリスト形式で出力する
MantissaExponent[x,b]
b 進法表記を使い仮数部と指数部をリスト形式で出力する
仮数部と指数部への数の分解
実数を仮数部と指数部に分解しリスト形式で出力する：
厳密値と近似値
普通の電卓では，例えば，10桁精度で計算が行われる．一方，Wolfram言語では厳密な結果を得ることができる．
の値を計算すると，31桁の大きな数だが，厳密な値が得られる：
電卓で値が得られるような近似値を求めることもできる．それには，式の後に//Nを続けて入力する．Nは数値を意味する語Numericalの頭文字を取ったもので，大文字でなければいけない．二重スラッシュ // の意味は「式の特殊な入力法」で説明する．
この入力で近似値が得られる：
式は通分され，結果は厳密な有理数として返される：
結果の近似値を得たいときは //Nを付け加える：
expr//N
式 expr の近似値を返す
数値近似
例えば，7と整数を入力すると，それは厳密なものとして扱われる．しかし，4.5と小数点を明記して入力すると，それは一定の精度の近似値として扱われる．
厳密な有理数とみなされ，既約分数が求められる：
小数を含む計算では，結果は近似値で与えられる：
この例でも小数点を明示したので，結果は近似値である：
式中にひとつでも小数があれば，最終的な結果は近似値となる：
数値の精度
「厳密値と近似値」で触れたが，Wolfram言語はどんな桁精度の実数でも扱える．ここで，実数の精度とは一般に有効桁数の大きさを計る．一方，精度に似た尺度に確度という考えがある．実数近似値において確度とは小数点以下の桁数の大きさを計る．つまり，精度は数値の相対誤差の大きさを計り，確度は絶対誤差の大きさを計る．数の扱いが完全に首尾一貫するためには，精度と確度の値が整数桁に対応しないことがしばしばある．
Precision[x]
数 x の10進法表記の有効桁数
Accuracy[x]
数 x の10進法表記の小数点以下の有効桁数
実数の精度と確度
30桁精度の数を生成する：
数の桁精度を調べる：
何桁かだけが小数点の右側になっているので確度は低い：
この数は桁すべてが小数点の右側になっている：
確度が精度よりも大きくなっている：
近似実数の値には見えない桁に関連する不確かさが常に付きまとう．精度をこの不確かさの相対的な大きさの尺度と考えることもできる．確度はこの不確かさの絶対的な大きさの尺度である．
Wolfram言語は数 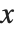の不確かさが 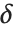であればその真値は 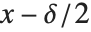から 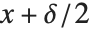までの大きさ 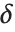の区間のどこかにあるように設定されている．確度が 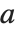の近似値の不確かさはで，精度 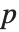の非零の近似値の不確かさは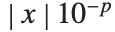であると定義される．
Precision[x]
Accuracy[x]
不確かさについての精度と確度の定義
不確かさよりも小さな量を足したり引いたりしても目に見える影響は出ない：
N[expr,n]
任意精度の数を使って expr を n 桁まで評価する
N[expr]
機械精度の数を使って expr を数値的に評価する
任意精度数と機械精度数による数値計算
Wolfram言語は「任意精度」数と「機械精度」数，すなわち「機械数」の2種類の近似実数を区別する．任意精度数は何桁でもよく，精度の情報も保っていられる．一方機械数は常に同じ桁数で精度情報も持たない．
これは を機械数に近似したものである：
これは両方とも任意精度数である：
以下でより詳しく説明するが，機械数は使用しているコンピュータシステムの数値機能を直接使用するものである．結果として，これを使うと計算が速くできることが多い．しかし任意精度数に比べて柔軟性は低く，結果が正しいかどうかの判断に難解な数値解析等が必要なことがある．
MachinePrecision
機械数を示す精度指定
$MachinePrecision
使用しているコンピュータシステムの機械数で有効な精度
MachineNumberQ[x]
x が機械数かどうかの検証
機械数
これは機械数を示す記号MachinePrecisionを返す：
このコンピュータの機械数は16桁より若干劣る：
近似実数の入力があると，機械精度数としてか，それとも，任意精度数として扱うかをWolfram言語内部で選択しなければならない．特に指定しない限り，Ceiling[$MachinePrecision+1]の桁長より短い桁長で実数を入力したならば，機械精度が使われ，その反対に，より長い桁長で入力したならば，任意精度が使われる．
123.4
機械精度の数
123.45678901234567890
コンピュータシステムによっては任意精度の数として扱われる
123.45678901234567890`
すべてのコンピュータシステムでの機械精度の数
123.456`200
任意精度（この場合は200桁精度）の数
123.456``200
任意精度（この場合は200桁確度）の数
1.234*^6
科学表記法の機械精度の数 (1.234×106)
1.234`200*^6
科学表記法の200桁精度の数
2^^101.111`200
200桁精度の2進数
2^^101.111`200*^6
科学表記の2進数 (101.1112×26)
数の入力形式
計算が終了し答が出力されるとき，読みやすさのため桁長が調整される．こうして出力された答は精度が落ちている可能性があるので，再度入力として使う場合は注意が必要である．求めた答を入力として使いたいときは，入力形を答に作用させ，桁精度調整前の情報が失われていないことを確認する必要がある．
標準出力形を使っている場合，この例にあるように答は6桁になってしまう：
入力形にすると，Wolfram言語が現時点で認識している全桁が得られる：
任意精度の数を標準出力形で出力する：
入力形を使うと，現行の桁精度を特別に表示できる．さらに，必ず現行精度で数を再構築できるよう指定した以上の桁精度で答を出力する：
こうすると桁長の表示はされない：
InputForm[expr,NumberMarks->True]
有限精度の実数末尾にナンバーマーク( ` )を付け数値の桁長を明示する
InputForm[expr,NumberMarks->Automatic]
任意精度の数のみにナンバーマーク( ` )による桁長表示を行う
InputForm[expr,NumberMarks->False]
ナンバーマーク(`)桁長表示を禁止する
数の出力形の制御
上記InputFormや後述のToStringとOpenWrite等の数の表記にかかわる関数において，オプションNumberMarksのデフォルト設定は$NumberMarksの値で定められる．したがって，$NumberMarksを設定し直すことによってInputFormを使った数の表記方法をすべて変更できる．
以下により，Wolfram言語はデフォルトで入力形式にナンバーマークを含むようになる：
常時表示にしたので，機械精度の答にもナンバーマークが付け加えられる：
ナンバーマークを禁止しても，InputFormを使うと記号*^を使った科学表記で答が表示される：
数値計算ではときには望んでいる精度以下の結果しか得られないことは避けられないことである．特に，ゼロに非常に近い値が得られたときには，その値をゼロと仮定してよいような場合がある．このときにはChopを使うとゼロに非常に近い近似値を整数0で置き換えることができる．
Chop[expr]
式 expr に含まれる10-10未満の実数近似値を0に置き換える
Chop[expr,dx]
dx 未満の実数近似値を0に置き換える
ゼロに近い端数の除去
この例の計算をすると虚数部に非常に小さい値が生じる：
Chopを作用させ答から虚数部を除去する：
任意精度の計算
Wolfram言語では，//Nを使った数値近似の計算は電卓と同じように行われる．つまり，決まった一定の精度で計算が行われる．これに対して，有効数字を指定して任意な桁精度で計算させることもできる．このため，Wolfram言語では，数値計算の結果をどのような精度でも得ることができるのである．
expr//N または N[expr]
式 expr を固定桁精度で数値近似
N[expr,n]
式 expr を n 桁精度で数値近似
数値評価関数
を固定桁精度で表示させる．N[Pi]はPi//Nと同じである：
を40桁精度で表示させる：
を30桁精度で表示させる：
どんな計算でも数値処理をすれば，必ず，丸め誤差が結果に入ってしまう．数値計算の精度を高めれば，これに比例して誤差も小さくなる．精度を高めていって，同一の答が得られることが確かめられれば，結果が正しいかどうかの確認になる．
は整数に非常に近い値である．整数でないことを確認するには十分に高い桁精度で値を表示させる必要がある：
任意精度の数
計算が任意精度を持つ数に基づいて行われるとき，精度管理が全計算過程において取られる．そうすることで，入力値の精度に基づく最高精度で答が通常求まる．
Wolfram言語内部では，任意精度の数には有効な桁長は任意で限られた数しかなく，他の桁は未知である，とされる．一般に，任意精度の数 x は確定している有効数字（Precision[x]の返す桁数）とそれに続く全く不確定な無限桁長の数字からなるものとして扱われる．
これは を10桁精度で計算する：
ある点を過ぎるとすべての桁が曖昧になる：
式が入力され計算が始まると，計算結果のどの数字が入力値の持つ不確定な数字に影響されるか検討がなされる．そして影響を受けた数字が含まれないように精度が設定される．その結果，不確定な数字がどんな値であろうと，Wolfram言語が出力する数字はすべて正しいものであることが保証される．
を30桁精度で計算する：
結果は厳密に30桁の精度である：
数桁精度の値を入力すると，答の精度が落ちていることが分かる：
引数が近似値でなく厳密な値142/1000であるならば，これをはっきりしなければいけない：
多くの計算問題で「丸め誤差」や「桁落ち誤差」が原因となり，計算ステップが重なるにつれ答の精度が次第に落ちてしまうことがある．このうち「桁落ち誤差」はほとんど同じ値を持った2つの数の差を取るときによく起る．接近した2数の差はその有効数字のうち末尾の方だけによって定まるが，一般的に，差を取る前の数に比べ答の有効数字の桁は非常に少なくなってしまう．
両入力値とも有効数字は20ある．しかし，答の精度はずっと低くなる：
差を取る片方の数だけ桁精度を上げても，答の精度は上がらない：
関数の出力精度は引数の持つ精度（入力精度）に複雑な形で依存する．変化の激しい挙動を持つ関数は一般に出力精度が劣る．なぜかというと，同じ誤差を持つ引数を入力したら，変化の小さい関数に比べ，関数値により大きな出力変動幅が出てしまうからである．これに対して，定数関数に近い関数は入力精度より高い精度で関数値を返すときがある．
これは，出力精度が入力精度より劣った例である：
の値を20桁精度で計算する：
厳密な整数値1を加えると答がより高い精度を持つようになる：
一般に，同じ計算をいくつかの違う方法で行うと，精度が違った答が得られてしまうことを認識しておく必要がある．桁精度は1度失ったら取り戻せない．これは情報を失うことである．
40桁精度で1に近い値を持つ数を定義する：
整数値1を加算しても桁精度は落ちない：
確認してみると，40桁のままである：
この例の式は，実は，1+xの値と同じ計算をするが，この式を使うと精度が落ちてしまう：
やはりかなり精度が落ちてしまっている：
上の例にもあったように，同じ計算をしても演算法を変えると違った近似値が答として求まってしまうときがある．このことから，2つの近接値の比較をするときは十分な注意を払う必要があると言える．Wolfram言語が2つの実数が等しいかどうかを判定するときは実効的な差を取る．そして，差が入力精度的に許容される幅の中にあるかどうか判定する．許容幅に収まる場合は「ゼロに一致」と解釈する．
2つの数は指定した桁精度内で等しい：
数学関数の計算に使うWolfram言語の内部アルゴリズムは，答の精度をなるべく高く保つように作られている．Wolfram言語の組込み関数を使っている限り，通常，入力精度に対応する最高の精度で答が得られる．しかし場合によっては期待するほど高い精度で答は返ってこない．これは，内部処理的に高い精度で処理を続けることが不可能になり，Wolfram言語が計算精度を下げて処理したため起ってしまう．もちろん，引数の有効数字を増やし，入力精度を上げておけば，Wolfram言語の内部処理がより高い精度で実行できるため，多くの場合，答の精度もそれにつられて高くなる．
N[expr]
式 expr を数値解析的に計算し機械精度で答を出力する
N[expr,n]
式 expr を数値解析的に計算し最高 n 桁精度で答を出力する
数値計算と桁精度
整数とその他の厳密数値要素のみで構成される式が第1の入力式であれば，N[expr,n]を使い，ほとんどの場合，指定通り n 桁精度で答を得られるであろう．ここで注意してほしいのは，高い桁精度で答を出すということは，ときには，内部の中間計算はそれ以上の精度で行われなければならない，ということである．
この中間処理で許容する補助的な有効数字を指定・変更するには，大域パラメータである$MaxExtraPrecisionの値を変えればよい．
変数
デフォルト値
$MaxExtraPrecision50
使用する追加的最大精度
中間計算の精度管理
Wolfram言語は正しい答を得るために自動的に内部精度を上げる：
デフォルト設定の$MaxExtraPrecision=50では，Wolfram言語は正しい答を出せない：
このようにしてWolfram言語に，内部計算でもっと桁数を使ってもよいと指示する：
正しい答が出せるようになった：
$MaxExtraPrecisionをデフォルト値に設定し直す：
計算に厳密な数を使っていても，内容によっては内部処理の一部で近似値が使われることがある．このため，$MaxExtraPrecisionの設定値によっては，厳密な値を使っていても精度の低下が起る場合がある．
近似値から得られる境界値が使われ式が評価される：
デフォルトの$MaxExtraPrecisionの設定ではこの式は計算できない：
$MaxExtraPrecisionの設定を臨時に変更する．今度は計算できる：
精度を低下させる計算をすると，結果の数に有効桁が全くない可能性もある．しかし，そのような場合でもなお，Wolfram言語はその数の確度に関する情報を保っている．有効数字はないが確度が a である数を与えられると，Wolfram言語はその数の実際の値が範囲{-10-a,+10-a}/2にあることが示せる．Wolfram言語はデフォルトによりそのような数を0.×10eという形で出力する．
これは20桁精度の数である：
ここには有効桁がない：
それでもWolfram言語は結果の確度を記録している：
この結果を厳密な1に加えるとかなり高精度の数が与えられる：
数をその精度で特徴付ける難しさは，ゼロと一致する数ならどれでも精度がゼロであるとして扱われる点である．そのような数の既知の桁はすべてゼロなので有効であるとみなし得る桁がないというのがその理由である．
これは値がゼロと一致する数である：
この数には精度の有効桁と見なせる桁がない：
しかし，この数にはこの数の不確かさを特徴付ける確かな確度がある：
結果がゼロ付近になりそうな計算をするときは所望の精度ではなく確度を指定した方がよいかもしれない．
N[expr,p]
精度 p で expr を評価する
N[expr,{p,a}]
最高精度 p， 確度 a で expr を評価する
N[expr,{Infinity,a}]
任意精度，確度 a で expr を評価する
確度と精度の指定
これは記号式である：
これは式がゼロに等しいことを示している：
Nは結果が精度20であることを保障できない：
しかし確度20の結果を得ることはできる：
任意精度の数に現れる不確定数字を扱うときに，Wolfram言語は異なる2数の不確定数字は互いに完全に独立であると仮定する．その理由は追って説明するが，そうしておけば，答の精度が不正に高くなるというようなことは起らなくなる．しかし，同時に，不必要に精度を下げてしまうこともある．
特に，ある計算で2つの数が同じ処理で生成される場合には，不確定桁のうちのいくつかが同じ値を持つ可能性がある．そして，差を取ると，不確定桁が実際には消えてしまうという場合も起り得る．ところが，Wolfram言語では，不確定桁は常に独立しているという前提を取っているので，本来なら行われるべきキャンセル処理をしないという可能性もある．
20桁精度で計算する：
1+dの計算値はおよそ34桁精度である：
この値では精度が劣る．各々の入力変数dの持つ不確定桁は独立であるという前提で計算処理を進めたからである：
数値計算アルゴリズムは，場合によっては，式中の数と数で不確定桁がキャンセルすることで答の精度を上げている．もし不確定桁がいずれキャンセルする，ということが事前に分かっているならキャンセルする不確定桁の代りに固定桁を追加しておくとよい．計算で確定桁がキャンセルすることによって，桁精度の向上した答が得られる．
SetPrecision[x,n]
必要な数だけ2進値のゼロの桁数字を付け加えることで，数値から n 桁精度の値を作成する
SetAccuracy[x,n]
n 桁精度の確度を持つ値を作成する
精度と確度を変更する関数
dに桁10個を付け足す：
こうすれば付け足した桁はキャンセルする：
答の精度は約44桁ある．前は34桁だった：
SetPrecisionは2進値ゼロの桁を必要数付け足すことで数の精度を上げる．ただし，計算によっては，Wolfram言語が表示する桁数より多い桁を任意数導入するようになっている．そのようなときは，SetPrecisionではゼロの桁を追加する前にWolfram言語が入れた桁を使う．
40桁精度の実数を作る．任意に付け足す桁は2進値ゼロとして導入される：
変数
デフォルト値
$MaxPrecisionInfinity
使用する最大合計精度
$MinPrecision0
使用する最低精度
大域精度管理パラメータ
$MinPrecision=n と大域定義をすることで，実効的に，SetPrecision[expr,n]で行う任意精度の設定を計算するすべてのステップに適応することができる．これは，n 桁以下の有効数字を持つ任意精度の数には，全桁数が常に n になるようゼロ桁が自動的に付け足される，ということを意味している．
$MaxPrecision=n と$MinPrecision=n の両方を設定しておくと，任意精度の数ならどんな数でも n 桁長の固定精度を持つように強制することができる．つまり，Wolfram言語に，任意精度の数を機械精度の数と同じように扱うように指示することになる．もちろん，通常の機械精度より桁精度を上げてだ．
固定桁精度にすると，計算処理によっては効率が上がることがある．しかし，注意深い分析をしないと，答が出てもどの桁までが実際に正しいのか不明である．
20桁精度の小さい値を持つ数を例に取る：
普通の計算をする．問題なく答を出してくれる：
固定桁精度で計算するように命令する：
最初の数桁は正しいが残りは正しくない：
機械精度の数値
計算式にひとつでも機械精度の数があると，その式のすべての計算は機械精度で行われ，答は機械精度で出てくる．
1つでも機械精度の入力数値があると，すべて機械精度で計算される：
Zeta[5.6]は機械精度の値を返すので，Nがこの場合あってもなくても答は機械精度の数値で出てくる：
今度は，高い精度で答を得ることができる：
任意精度の数を用いて計算するとき，「任意精度の数」で説明してあるように，Wolfram言語内部で常に計算結果の桁精度がどのステップでいくつあるか監視される．そして，入力値の精度に応じて，正確に判明している桁だけが答として出力される．しかし，機械精度の数で計算をする場合は事情が違ってくる．つまり，入力値の精度に基づいて計算結果の全桁が決定できたとしてもWolfram言語は常に機械精度の桁数でしか答を出さない．
機械精度を持った2つの数の差を取る：
桁精度を確認してみると，機械精度になっている：
実際に確定した桁をすべて表示する：
Wolfram言語で機械精度の数値計算をすると，ちぐはぐな桁が発生するという事実は望ましいことではない．しかし，固定桁精度を使う最大の理由は計算効率を高めるということにある．
ユーザがコンピュータシステムの詳細を調べる必要がないようにWolfram言語は設定されている．とはいっても，もし，Wolfram言語がコンピュータの持つ実数演算機能を最大限に利用していないと，機械精度の数を扱った計算で大きな損失が出てしまう．
ほとんどのコンピュータは特定の固定桁精度で浮動点数値計算を実行するための特殊なハードウェア，または，マイクロコードを備えていている．機械精度で数値計算をする際に，それらの機能をWolfram言語は最大限利用する．
Wolfram言語の動作するコンピュータでは，Wolfram言語において機械精度とされる数値は，倍精度の浮動点数値として表される．現在使われているほとんどのコンピュータでは，倍精度の数は64ビットの情報量を持っており，10進法で16桁の仮数部からなる．
コンピュータに組み込まれた浮動点機能を使う最大の理由はスピードである．そのような機能を直接使わない任意精度の数値計算は普通，機械精度の計算に比べ何倍も遅い．
組込み演算機能を使うと悪い点もある．すでに説明したが，そのひとつは，適切な桁精度が別にあっても，計算に使うすべての数が固定桁精度に強制されることである．
2つ目の悪い点は，コンピュータが違えば機械精度の数は違った扱いを受ける可能性があることである．機械精度の数を使うとき，Wolfram言語はコンピュータの演算システムの言いなりにならざるを得ない．もし，浮動点の演算処理を違った方法で行うコンピュータを使ったなら，Wolfram言語で行う機械精度の計算は微妙に違った結果が得られることもある．
$MachinePrecision
10進法表記の桁精度の桁長
$MachineEpsilon
1.0に加えて得られる値が1.0に等しくなくなる最小の機械精度の正の数
$MaxMachineNumber
機械精度の最大値
$MinMachineNumber
正規化された形式で表すことのできる機械精度の正の最小値
$MaxNumber
任意精度の数の取り得る最大値
$MinNumber
任意精度の正の数の最小値
あるコンピュータシステムにおける数の特徴
コンピュータシステムが何であれ，機械精度の数は特定の2進ビットの固定数で表される．このため，非常に近い値を持った数が2つあると，両者は全く同じビットパターンを持ってしまい，区別ができなくなる．使っているコンピュータで，1.0の値に最も近似で，かつ，異なった2進表記の数が何かを調べることができる．両者の値の差がパラメータ$MachineEpsilonに割り付けられているので，このパラメータを参照すればよい．
この本の例題の計算に使っているコンピュータシステムの$MachineEpsilonの値を確認する：
返ってくる精度値は1.であるが，Wolfram言語は実際の値がそれより大きいことを知っている：
InputFormを使うと結果が厳密な1ではないことが分かる：
1を引き，$MachineEpsilonを得る：
これもまた1.の答が返ってくる：
この場合は，機械精度で結果は1.とはっきり区別できない：
結果から1を引くと0が返される：
機械数は限定した桁精度しか持たないだけでなく，大きさも限定される．$MaxMachineNumberより大きい数を生成する場合は，Wolfram言語内部で自動的にその数が任意精度に変換される．
この例で使ったコンピュータシステムの扱える機械精度で表せる最大値を参照する：
Wolfram言語は$MaxMachineNumberより大きな結果を自動的に任意精度に変換する：
次の計算では結果が機械精度数の範囲外になっている：
バージョン11.3では，機械精度の計算で$MinMachineNumberより大きさの小さい数が生成される場合，Wolfram言語が警告を出力するようになった．しかし，その結果は二進の仮数で先頭にゼロを持つ非正規の機械数として保持される．
次は，この例題に使われたコンピュータシステム上で正規形式に変換された最小機械精度数である：
Wolfram言語は$MinMachineNumberよりも小さい数になる計算について警告メッセージを発するが，自動的に任意精度計算には変換しない．
有効数字をすべて失って，最終的に機械数ゼロの答になることもある：
SetPrecisionを使って任意精度に変換すると，このアンダーフローを回避することができる：
区間演算
Interval[{min,max}]
min から max までの区間（閉区間）
Interval[{min1,max1},{min2,max2},…]
min1から max1まで，min2から max2まで，…の区間の和集合
実数の区間の表記法
との間のすべての数を表す：
との間にある数の2乗は必ずからの間にある：
逆数を計算すると，2つの区間が返ってくる：
Absを作用させると，区間を数直線の正の側に折り返す：
区間をいろいろな種類の関数計算に使ってもよい：
ある種の関数は自動的に区間を返す：
IntervalUnion[interval1,interval2,…]
複数の区間の和集合
IntervalIntersection[interval1,interval2,…]
複数の区間の共通部分
IntervalMemberQ[interval,x]
区間に点 x が含まれるかどうかを判定する
IntervalMemberQ[interval1,interval2]
区間 interval2が区間 interval1の中に完全に含まれるかどうかを判定する
区間に関する操作
2つの区間の交差する部分を探す：
MaxとMinを使い区間の端を探す：
7がどの区間に含まれるか判定させる：
厳密な値に対してだけでなく近似値に対しても区間が使える．機械精度の数であっても答が有効になるように内部で四捨五入処理が施される．
機械精度で0.に四捨五入される区間を表示する：
100.近傍に相当する区間を表示する．これはゼロのまわりまで平行移動したものを示す：
どんな桁精度の数でも同様な処理を行える：
普通の機械精度の計算では，この例の値は間違って計算される：
しかし，ここで生成する区間は正解である0を含む：
不定形・無限大
0/0のような式を入力すると，答が不確定とのメッセージが表示される．答の値としてはIndeterminateが返ってくる：
0/0のような式は，数値的な計算をすると不確定（不定形）な結果になる．ただ，0/0と入力しても，どのような答をユーザが期待しているかWolfram言語には全く分からない．もし，で 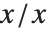の極限を計算させ，結果的に0/0が発生するなら，必要な答は1であろう．また，もし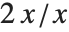， の極限を計算するなら，ほしい答は2であろう．式0/0だけでは十分な情報を持っていないので，正解が上記の極限か，または，他の演算法で得られる答なのか限定できない．実際に計算させると，答は不確定なもの(indeterminate)として返ってくる．
演算計算で結果が不確定になるときは，警告メッセージが表示され，計算の答として不確定な値Indeterminateが返される．Indeterminateを別の式で使うとその答もまたIndeterminateになる．不確定な結果が一度でも発生すると，続く演算はおかしくなってしまう（Wolfram言語で使うIndeterminateは，IEEE浮動点規格における「数でない」オブジェクトに相当する）．
Indeterminateの演算には，通常の簡約化の規則は当てはまらない：
演算が何であっても，1つIndeterminateがあると不確定な結果になる：
計算プログラムを書いているとき，計算を進めていく上で，不確定な結果が発生したかどうか判断できるかどうかが多くの場合重要になる．この判断をするには，「メッセージ」で触れた関数Checkが使える．この関数は不確定結果に関して警告メッセージの出力があったかどうかを判定するのに使う．
プログラムの中にCheckを入れておき警告が発せられたか，確認ができる：
Indeterminate
不確定な数値計算の結果
Infinity
正の無限大
-Infinity
負の無限大 ( DirectedInfinity[-1] )
DirectedInfinity[r]
複素数 r 方向の無限大
ComplexInfinity
複素平面上で不確定な方向性を持った無限大（無限遠点）
DirectedInfinity[]
ComplexInfinityに同等
不確定な値と無限大
計算で無限な値を扱えると便利な場面が多くある．代数記号Infinityは正の無限大を表す．これを使って和や積分の区間(limits)が指定できる．さらに，無限大を演算の中で直接使える場合もある．
積分の端点が無限大の例：
Wolfram言語は無限大の逆数はと分かっている：
無限大と無限大の差は不確定である：
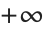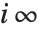無限大を扱うときには微妙な問題がいくつか発生する．1つは無限大の方向に関する．無限大の積分を計算するとき，通常，複素平面上のある一定方向の無限大までの経路で積分することを考える．その場合，違った方向を取れば違った無限大になる，ということを認識することが重要である．例えば，同じ無限大でも と があるように，場合によっては， 等の無限大が必要になることもある．
Wolfram言語では無限大に複素数の表す方向を与えることができる．正の無限大Infinityを入力したなら，内部ではDirectedInfinity[1]の形に変換される．この形では無限大は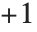 の方向にある点を示す．同様に，-InfinityはDirectedInfinity[-1]として扱われ，IInfinityはDirectedInfinity[I]になる．常にDirectedInfinityの形で内部処理が行われるが，出力形としてはDirectedInfinity[r]がr Infinityを使った記述に再変換される．
InfinityはDirectedInfinity[1]に内部で変換される：
方向性を持つ無限大という考え方は便利ではあるが，そのような値が常に結果として得られるとは限らない．例えば，1/0と入力し，無限の値が答として返ってきても，その無限の方向を知ることはできない．1/0の値は計算するとDirectedInfinity[]として返ってくる．また，標準的な出力形では不確定方向の無限値はComplexInfinityと表示される．
1/0と入力すると，不確定方向の無限大（いわゆる無限遠点）が返ってくる：
数値計算の抑制
NHoldAll
関数のどの引数もNの影響を受けないようにするN
NHoldFirst
最初の引数が影響を受けないようにする
NHoldRest
最初の引数以外の引数が影響を受けないようにする
数値計算を抑制する属性
通常，Nは関数の内部に入り，引数ひとつひとつに作用する：
fの最初の引数にはNを適用しないように命じる：
fの最初の引数は厳密な値のまま残される：