DiscreteWaveletPacketTransform[data]
配列 data の離散ウェーブレットパケット変換(DWPT)を与える.
DiscreteWaveletPacketTransform[data,wave]
ウェーブレット wave を使って離散ウェーブレットパケット変換を与える.
DiscreteWaveletPacketTransform[data,wave,r]
r レベルの細分化を使って離散ウェーブレットパケット変換を与える.




DiscreteWaveletPacketTransform
DiscreteWaveletPacketTransform[data]
配列 data の離散ウェーブレットパケット変換(DWPT)を与える.
DiscreteWaveletPacketTransform[data,wave]
ウェーブレット wave を使って離散ウェーブレットパケット変換を与える.
DiscreteWaveletPacketTransform[data,wave,r]
r レベルの細分化を使って離散ウェーブレットパケット変換を与える.
詳細とオプション




- DiscreteWaveletPacketTransformはDiscreteWaveletDataオブジェクトを与える.
- DiscreteWaveletData dwd の特性は dwd["prop"]で求まる.使用可能な特性のリストは dwd["Properties"]で求まる.
- DiscreteWaveletPacketTransformは,ウェーブレットの完全木が計算されたDiscreteWaveletTransformを一般化したものである.
- data は任意の深さの矩形配列である.
- data は次のいずれでもよい.
-
list 任意階数の数値配列 image 任意のImageオブジェクト audio AudioオブジェクトまたはサンプルされたSoundオブジェクト - 使用可能なウェーブレット wave
-
BattleLemarieWavelet[…] Bスプラインに基づいたBattle–Lemariéウェーブレット BiorthogonalSplineWavelet[…] Bスプラインに基づいたウェーブレット CoifletWavelet[…] Daubechiesウェーブレットの対称性変種 DaubechiesWavelet[…] Daubechiesウェーブレット HaarWavelet[…] 古典的なHaarウェーブレット MeyerWavelet[…] 周波数領域で定義されるウェーブレット ReverseBiorthogonalSplineWavelet[…] Bスプラインに基づいたウェーブレット( 逆双対ウェーブレットと主ウェーブレット) ShannonWavelet[…] シンク関数に基づいたウェーブレット SymletWavelet[…] 最小非対称直交ウェーブレット - デフォルトの wave はHaarWavelet[]である.
- 細分化レベル r の設定値を高くすると,スケールの大きい特徴が解決される.
- デフォルトの細分化レベル r は
![min(TemplateBox[{{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, n, )}, +, {1, /, 2}}}, Floor],4) min(TemplateBox[{{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, n, )}, +, {1, /, 2}}}, Floor],4)](Files/DiscreteWaveletPacketTransform.ja/1.png) で与えられる.ただし,
で与えられる.ただし,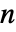 は data の最小次元である.
は data の最小次元である. - 細分化レベルが Fullのとき,r は
![TemplateBox[{{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, n, )}, +, {1, /, 2}}}, Floor] TemplateBox[{{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, n, )}, +, {1, /, 2}}}, Floor]](Files/DiscreteWaveletPacketTransform.ja/3.png) で与えられる.
で与えられる. - レベル
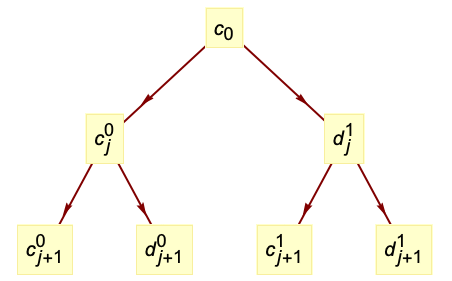
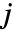 のウェーブレット係数の木は,粗い係数
のウェーブレット係数の木は,粗い係数 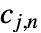 と詳細化係数
と詳細化係数 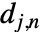 からなる.
からなる.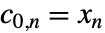 は入力 data を表す.
は入力 data を表す. - 前方変換は
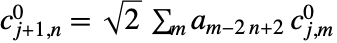 ,
, 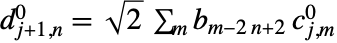 ,
, 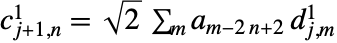 ,
, 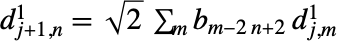 で与えられる.
で与えられる. - 逆変換は
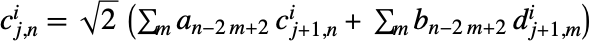 で与えられる.
で与えられる. 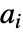 はローパスフィルタ係数で,
はローパスフィルタ係数で,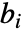 はハイパスフィルタ係数である.どちらも各ウェーブレット族で定義される.
はハイパスフィルタ係数である.どちらも各ウェーブレット族で定義される.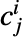 と
と 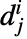 の次元は
の次元は ![wd_(j+1)=TemplateBox[{{{1, /, 2}, , {(, {{wd, _, j}, +, fl, -, 2}, )}}}, Ceiling] wd_(j+1)=TemplateBox[{{{1, /, 2}, , {(, {{wd, _, j}, +, fl, -, 2}, )}}}, Ceiling]](Files/DiscreteWaveletPacketTransform.ja/18.png) で与えられる.ただし,
で与えられる.ただし,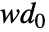 は入力 data の次元であり,fl は対応する wspec のフィルタ長である.
は入力 data の次元であり,fl は対応する wspec のフィルタ長である.- 使用可能なオプション
-
Method Automatic 使用するメソッド Padding "Periodic" 境界を越えてデータをどのように延長するか WorkingPrecision MachinePrecision 内部計算で使用する精度 - Paddingの設定値はArrayPadで使用できるものと同じである.
- InverseWaveletTransformは逆変換を与える.
- デフォルトで,InverseWaveletTransformは再構築に dwd["BasisIndex"]で表される係数を使う.WaveletBestBasisを使って最適化基底を計算し設定する.
例題
すべて開く すべて閉じる例 (3)
結果のDiscreteWaveletDataはウェーブレット係数の完全木を表す:
Imageオブジェクトを変換する:
スコープ (34)
基本的な用法 (5)
DiscreteWaveletDataオブジェクトから役に立つ特性を抽出することができる:
Normalを使ってすべてのウェーブレット係数を明示的に得る:
また,Allを引数として使ってすべての係数を得る:
Automaticを使って逆変換で使われる係数のみを得る:
"TreeView"または"IndexMap"を使ってどのウェーブレット係数が使えるかを見る:
ウェーブレット指標指定のリストに対応するいくつかのウェーブレット係数を抽出する:
ウェーブレット指標がパターンにマッチするすべての係数を抽出する:
WaveletBestBasisを使ってウェーブレットパケット係数の最適化基底を計算する:
計算された最良基底はデフォルトでWaveletListPlotのような関数で使われる:
ウェーブレット族 (10)
ベクトルデータ (6)
WaveletListPlotを使って,係数を共通の水平軸上でプロットする:
WaveletScalogramを使って係数を時間と細分化レベルの関数として可視化する:
マウスポインタが係数上に来ると係数指標がツールチップとして表示される:
データの最高の木としての表現のWaveletScalogram:
分解可能な最高の周波数(ナイキスト(Nyquist)周波数)で振動するデータ:
小さくないのは最初の詳細化係数{1}とその粗い子係数{1,0,0,…}のみである:
粗い係数{0,…}はデータと同じ大きいスケールの構造を持つ:
行列データ (5)
WaveletMatrixPlotを使ってさまざまなウェーブレット係数を可視化する:
最高の木表現のWaveletMatrixPlot:
二次元では,各方向のフィルタリング操作のベクトルが計算できる:
これらのベクトルを二進数展開として解釈するとウェーブレット指標の数が得られる:
Haarウェーブレットのローパスフィルタとハイパスフィルタを得る:
すべての水平および対角の詳細化係数,つまりウェーブレット指標{___,2|3,___}は0である:
配列データ (2)
画像データ (3)
一般化と拡張 (3)
DiscreteWaveletPacketTransformは記号的な量の配列に使うことができる:
オプション (5)
Padding (2)
WorkingPrecision (3)
デフォルトで,WorkingPrecision->MachinePrecisionが使われる:
WorkingPrecision->∞を使って厳密計算を行う:
アプリケーション (3)
特性と関係 (11)
DiscreteWaveletPacketTransformはウェーブレット係数の完全木を計算する:
DiscreteWaveletTransformは係数の完全木のサブセットを計算する:
DiscreteWaveletPacketTransform係数は各細分化のレベルで長さを半分にする:
StationaryWaveletPacketTransform係数はもとのデータと同じ長さである:
多次元離散ウェーブレット変換は一次元パケット変換と関連している:
Haarウェーブレット(デフォルト)でデータ長![]() の場合,計算される係数は等しい:
の場合,計算される係数は等しい:
デフォルトの細分化はMin[Round[Log2[Min[Dimensions[data]]]],4]で与えられる:
双直交ウェーブレット族では,エネルギーノルムは近似的に保存される:
HaarWaveletは平均すること(ローパスフィルタ)と差分を取ること(ハイパスフィルタ)に相当する:
DiscreteWaveletPacketTransformと比較する:
Haarウェーブレットのローパスフィルタとハイパスフィルタ:
HaarWaveletを使ってDiscreteWaveletPacketTransformと比較する:
もと画像のDiscreteWaveletPacketTransformの{0}係数と比較する:
テキスト
Wolfram Research (2010), DiscreteWaveletPacketTransform, Wolfram言語関数, https://reference.wolfram.com/language/ref/DiscreteWaveletPacketTransform.html (2017年に更新).
CMS
Wolfram Language. 2010. "DiscreteWaveletPacketTransform." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/DiscreteWaveletPacketTransform.html.
APA
Wolfram Language. (2010). DiscreteWaveletPacketTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteWaveletPacketTransform.html
BibTeX
@misc{reference.wolfram_2025_discretewaveletpackettransform, author="Wolfram Research", title="{DiscreteWaveletPacketTransform}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteWaveletPacketTransform.html}", note=[Accessed: 10-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_discretewaveletpackettransform, organization={Wolfram Research}, title={DiscreteWaveletPacketTransform}, year={2017}, url={https://reference.wolfram.com/language/ref/DiscreteWaveletPacketTransform.html}, note=[Accessed: 10-March-2026]}