InfiniteLine
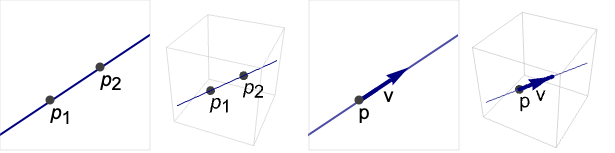
InfiniteLine[{p1,p2}]
表示经过点 p1 和 p2 的无限长直线.
InfiniteLine[p,v]
表示经过点 p,方向为 v 的无限长直线.
更多信息

- InfiniteLine 也被称为线.
- InfiniteLine 可被用作几何区域及图形基元.
- InfiniteLine 表示线性曲线
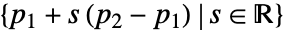 或
或 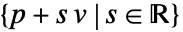 .
. - Hyperplane[n,p] 是在 2D 中使用法线 n 的替代表示.
- InfiniteLine 可用在 Graphics 和 Graphics3D 中.
- 进行渲染时 InfiniteLine 会被 PlotRange 修剪.
- 在图形中,点 p、pi 和矢量 v 可以是 Dynamic 表达式.
- 有些指令,比如 Thickness、Dashing 和着色会影响图形渲染.
- InfiniteLine 可与 GeometricScene 中的符号点一起使用.
范例
打开所有单元关闭所有单元基本范例 (3)常见实例总结
范围 (19)标准用法实例范围调查
图形 (8)
规范 (3)
坐标 (1)
点和矢量可以是 Dynamic 表达式:
区域 (11)
InfiniteLine 的度量为无限大:
应用 (17)用该函数可以解决的问题范例
将直线的截距式转换为 InfiniteLine:
将直线的点斜式转换为 InfiniteLine:
将直线的斜截式转换为 InfiniteLine:
将直线的两点式转换为 InfiniteLine:
将直线的参数式转换为 InfiniteLine:
参数式曲线 f[u] 的切线为 InfiniteLine[f[u],f'[u]]. 计算参数式曲线 ![]() 的切线:
的切线:
计算 InfiniteLine[{0,0},{1,1}] 和 InfiniteLine[{{0,1},{1,0}}] 的交点:
计算 InfiniteLine[{0,0},{1,1}] 和 Circle[{0,0},1] 的交点:
利用 BooleanCountingFunction 来表示恰好满足两个条件的情况:
计算 InfiniteLine[{{-1,1,1},{1,1,1}}] 和 InfinitePlane[{{2,0,0},{0,2,0},{0,0,2}}] 的交点:
计算 InfiniteLine[{{-1,1,1},{1,1,1}}] 和 Sphere[{0,0,0},3] 的交点:
计算 InfiniteLine[{{-1,1/3,1/2},{1,1/3,1/2}}] 和 Tetrahedron[{{0,0,0},{1,0,0},{0,1,0},{0,0,1}}] 的表面的交点:
可视化 RotationTransform 的旋转轴:
属性和关系 (5)函数的属性及与其他函数的关联
InfiniteLine[{p1,p2}] 等价于 InfiniteLine[p1,p2-p1]:
在二维空间,InfiniteLine[p,v] 等价于 Hyperplane[Cross[v],p]:
ParametricRegion 可以表示任意 InfiniteLine:
ImplicitRegion 可以表示任意 InfiniteLine:
InfiniteLine 是 ConicHullRegion 的一个特例:
文本
Wolfram Research (2014),InfiniteLine,Wolfram 语言函数,https://reference.wolfram.com/language/ref/InfiniteLine.html.
CMS
Wolfram 语言. 2014. "InfiniteLine." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/InfiniteLine.html.
APA
Wolfram 语言. (2014). InfiniteLine. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/InfiniteLine.html 年