KirchhoffGraph

KirchhoffGraph[kmat]

给出基尔霍夫矩阵（Kirchhoff matrix）为 kmat 的图.

KirchhoffGraph[{v₁,v₂,…},kmat]

给出顶点为 v_i 以及基尔霍夫矩阵为 kmat 的图.

更多信息和选项

KirchhoffGraph 也被称为拉普拉斯图.

KirchhoffGraph[kmat] 等价于 KirchhoffGraph[{1,2,…,n},kmat]，其中 kmat 的维度为 ×.
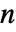KirchhoffGraph 采用和 Graph 相同的选项.

所有选项的列表

AlignmentPoint	Center	在图形内对齐的缺省点
AnnotationRules	{}	图、边和顶点的注释
AspectRatio	Automatic	高与宽的比
Axes	False	是否绘制轴
AxesLabel	None	坐标轴标签
AxesOrigin	Automatic	坐标轴原点
AxesStyle	{}	坐标轴样式指定
Background	None	绘图的背景色
BaselinePosition	Automatic	如何与环绕文本基线对齐
BaseStyle	{}	图形的基本样式指定
ContentSelectable	Automatic	是否允许进行内容选择
CoordinatesToolOptions	Automatic	坐标工具的详细行为
DirectedEdges	Automatic	是否将 Rule 解释为 DirectedEdge
EdgeLabels	None	边的标签和标签放置
EdgeLabelStyle	Automatic	边的标签所使用的样式
EdgeShapeFunction	Automatic	如何生成边的图形表示
EdgeStyle	Automatic	边的样式
EdgeWeight	Automatic	边的权值
Epilog	{}	主图形之后执行的图形指令
FormatType	TraditionalForm	文本的缺省样式类型
Frame	False	是否在图形周围放置边框
FrameLabel	None	边框标签
FrameStyle	{}	边框的样式指定
FrameTicks	Automatic	边框刻度
FrameTicksStyle	{}	边框刻度的样式指定
GraphHighlight	{}	要突出显示的图的元素
GraphHighlightStyle	Automatic	突出显示时使用的样式
GraphLayout	Automatic	如何设计顶点和边的布局
GridLines	None	绘制的网格线
GridLinesStyle	{}	网格线的样式指定
ImageMargins	0.	图形周围的边幅
ImagePadding	All	为标签等额外填充内容
ImageSize	Automatic	图形的绝对尺寸
LabelStyle	{}	标签的样式指定
Method	Automatic	使用图形方式的细节
PerformanceGoal	Automatic	优化的目标
PlotLabel	None	图形的一个整体标签
PlotRange	All	图形值的范围
PlotRangeClipping	False	是否在图形范围剪切
PlotRangePadding	Automatic	填充图形值范围的程度
PlotRegion	Automatic	填充的最后显示区域
PlotTheme	$PlotTheme	图的整体主题样式
PreserveImageOptions	Automatic	当显示相同图形的新版本时，是否保存图形选项
Prolog	{}	主图形之前执行的图形指令
RotateLabel	True	是否在边框上旋转 y 标签
Ticks	Automatic	坐标轴标记
TicksStyle	{}	坐标轴标记的样式指定
VertexCoordinates	Automatic	顶点的坐标
VertexLabels	None	顶点的标签和位置
VertexLabelStyle	Automatic	顶点的标签所使用的样式
VertexShape	Automatic	顶点的形状
VertexShapeFunction	Automatic	生成顶点的形状的函数
VertexSize	Medium	顶点的大小
VertexStyle	Automatic	顶点的样式
VertexWeight	Automatic	顶点的权值

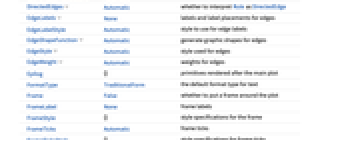
背景

KirchhoffGraph 基于表示无向或有向图的有效基尔霍夫矩阵而构造出一个图. 这里，有 n 个顶点的图对应的基尔霍夫矩阵是一个由图顶点度数及其邻接矩阵定义的 n×n 的方阵. 基尔霍夫矩阵在谱图理论中起着核心的作用，谱图理论是基于图邻接矩阵或基尔霍夫矩阵的特征值的对图的研究. 它也可被用于计算图中顶点之间的电阻距离，后者被定义为把每条图的边都替换为单位电阻后，顶点之间有效电阻的大小（当有电池与他们连在一起时）.
选项 DirectedEdges 可被用于指定构造的是无向图还是有向图. 默认情况下，若输入矩阵是对称的，那么 KirchhoffGraph 返回的是无向图否则返回的就是有向图. KirchhoffGraph 采用和 Graph 相同的选项.
对给定的图（包括用 KirchhoffGraph 构造的）的基尔霍夫矩阵可用 KirchhoffMatrix 返回. 类似的函数包括 AdjacencyGraph（从邻接矩阵构造图）、WeightedAdjacencyGraph 和 IncidenceGraph（从关联矩阵构造图）.

范例

打开所有单元关闭所有单元

基本范例 (2)

从基尔霍夫矩阵构建一个图：

一个对称基尔霍夫矩阵产生一个无向图：

范围 (6)

对称基尔霍夫矩阵解释为无向图：

非对称基尔霍夫矩阵解释为有向图：

使用 DirectedEdges 从对称矩阵构建一个有向图：

使用一个 SparseArray 对象来指定邻接矩阵：

默认情况下，顶点采用从 1 到 n 的整数值：

使用一个显式顶点列表来给出顶点名称：

KirchhoffGraph 对大规模矩阵起作用：

选项 (82)

AnnotationRules (3)

指定顶点的注释：

边：

图自身：

DirectedEdges (3)

默认情况下，一个对称矩阵生成一个无向图：

使用 DirectedEdges->True 来生成一个有向图：

默认情况下，一个非对称矩阵生成一个有向图：

EdgeLabels (7)

对边 12 添加标签：

对每个边分别添加标签：

使用任意表达式作为标签：

使用符号位置信息的 Placed 来控制沿着一条边的标签位置：

使用显式坐标来放置标签：

改变标签内的位置：

放置多个标签：

通过 Tooltip 和 StatusArea 的值，使用自动标签：

EdgeShapeFunction (6)

获取 EdgeShapeFunction 的内置设置列表：

包含基本线条的无向边：

具有各种符号的边线条：

包含实心箭头的有向边：

线型箭头：

开放式箭头：

对每条边指定一个边函数：

与一个不同的默认边函数合用：

通过运行程序，绘制边：

EdgeShapeFunction 可以与 EdgeStyle 合起来使用：

EdgeShapeFunction 具有比 EdgeStyle 更高的优先级：

EdgeStyle (2)

对所有边进行样式化处理：

对单条边进行样式化处理：

EdgeWeight (2)

指定所有边的权值：

将任意数值表达式作为权值使用：

GraphHighlight (3)

突出显示顶点 1：

突出显示边 23：

突出显示顶点和边：

GraphHighlightStyle (2)

获取 GraphHighlightStyle 的默认设置列表：

使用 GraphHighlightStyle 的内置设置：

GraphLayout (5)

缺省情况下，自动选择布局样式：

指定特殊曲线的布局：

指定满足最优标准的布局：

VertexCoordinates 覆盖 GraphLayout 的坐标：

用 AbsoluteOptions 来提取按布局算法得出的 VertexCoordinates：

PlotTheme (4)

基本主题 (2)

采用常见基本主题：

采用单色主题：

特色主题 (2)

采用大图主题：

采用经典的示意图主题：

VertexCoordinates (3)

默认情况下，自动计算任意顶点坐标：

使用 AbsoluteOptions 提取所得的顶点坐标：

指定沿着一个椭圆的布局函数：

使用它来生成顶点坐标：

VertexCoordinates 具有比 GraphLayout 更高的优先级：

VertexLabels (13)

将顶点名称作为标签使用：

对单个顶点添加标签：

对所有顶点添加标签：

将任意表达式作为标签使用：

使用具有符号位置信息的 Placed 来控制标签位置，包括内部位置：

拐角位置外的符号表示：

内部位置的符号表示：

内拐角位置的符号表示：

使用显式坐标来放置标签中心：

把所有标签放在顶点的右上角，并且在标签内改变坐标：

放置多个标签：

可以使用任意数目的标签：

使用 Placed 的变量来控制格式，包括 Tooltip：

或者 StatusArea:

使用更美观的格式函数：

VertexShape (5)

将任意 Graphics、Image 或者 Graphics3D 作为顶点形状使用：

对单个顶点，指定顶点形状：

VertexShape 可以与 VertexSize 合起来使用：

VertexShape 不受 VertexStyle 影响：

VertexShapeFunction 具有比 VertexShape 更高的优先级：

VertexShapeFunction (10)

获取 VertexShapeFunction 的内置设置列表：

利用 VertexShapeFunction 在 "Basic" 集合中的内置设置：

简单基本形状：

普通基本形状：

使用 VertexShapeFunction 在 "Rounded" 集合中的内置设置：

使用 VertexShapeFunction 在 "Concave" 集合中的内置设置：

绘制单个顶点：

与默认的顶点函数合起来使用：

使用预定义的图形绘制顶点：

通过运行程序，绘制顶点：

VertexShapeFunction 可以与 VertexStyle 合起来使用：

VertexShapeFunction 具有比 VertexStyle 更高的优先级：

VertexShapeFunction 可以与 VertexSize 合起来使用：

VertexShapeFunction 具有比 VertexShape 更高的优先级：

VertexSize (8)

默认情况下，自动计算顶点大小：

使用符号顶点尺寸，指定所有顶点的大小：

使用顶点坐标之间的最小距离的百分比：

对所有顶点坐标，使用整体对角线比率：

指定在和方向上的尺寸：

对单个顶点，指定大小：

VertexSize 可以与 VertexShapeFunction 合起来使用：

VertexSize 可以与 VertexShape 合起来使用：

VertexStyle (4)

对所有顶点进行样式化处理：

对单个顶点进行样式化处理：