LogMultinormalDistribution
LogMultinormalDistribution[μ,Σ]
母数が μ と Σ の多変量正規対数分布を表す.
詳細
- LogMultinormalDistribution[μ,Σ]はTransformedDistribution[Exp[{u1,u2,…,un}],{u1,u2,…,un}MultinormalDistribution[μ,Σ]]に等しい.
- LogMultinormalDistributionでは,μ は実ベクトルであり,Σは
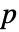 ×
×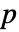 (ただし,p=Length[μ])の任意の正定値実数対称行列である.
(ただし,p=Length[μ])の任意の正定値実数対称行列である.
予備知識
- LogMultinormalDistribution[μ,Σ]は,
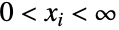 を満足するすべてのタプル
を満足するすべてのタプル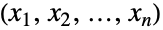 からなる
からなる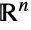 の部分集合上でサポートされ,
の部分集合上でサポートされ,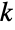 番目の周辺分布のそれぞれが
番目の周辺分布のそれぞれが 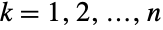 について正規対数であるという特性で特徴付けられる多変量連続統計分布を表す.言葉を変えれば,各
について正規対数であるという特性で特徴付けられる多変量連続統計分布を表す.言葉を変えれば,各 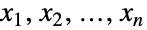 変数は
変数は 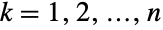 について xkLogNormalDistributionを満足する.多変量正規対数分布LogMultinormalDistribution[μ,Σ]は実数ベクトル μ とnLength[μ]Length[Σ]を満足し分布の合併平均,合併分散,合併共分散を定義する正定値対称行列 Σ でパラメータ化される.
について xkLogNormalDistributionを満足する.多変量正規対数分布LogMultinormalDistribution[μ,Σ]は実数ベクトル μ とnLength[μ]Length[Σ]を満足し分布の合併平均,合併分散,合併共分散を定義する正定値対称行列 Σ でパラメータ化される. - 多変量正規対数分布は,この分布が厳密に,座標が
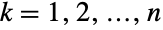 について
について 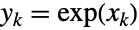 を満足する確率変量である確率変量ベクトル
を満足する確率変量である確率変量ベクトル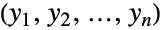 でありベクトルが
でありベクトルが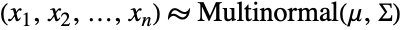 である分布であることから,この名前で呼ばれている.また,ベクトル
である分布であることから,この名前で呼ばれている.また,ベクトル 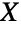 が正規分布に従う場合にベクトル
が正規分布に従う場合にベクトル 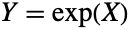 が多変量対数分布に従うことも,この名前の由来となっている.多変量対数正規分布の確率密度関数(PDF)は,絶対最大値を持つが,複数の「峰」(相対的極大値)を持つこともある.一般に,同伴周辺分布の各PDFは,周辺分布のPDFが
が多変量対数分布に従うことも,この名前の由来となっている.多変量対数正規分布の確率密度関数(PDF)は,絶対最大値を持つが,複数の「峰」(相対的極大値)を持つこともある.一般に,同伴周辺分布の各PDFは,周辺分布のPDFが 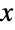 の大きい値に対して指数的というよりむしろ代数的に減少するという意味で「太い」(この動作はこれら周辺分布のSurvivalFunctionを分析することで量的に厳密にすることができる).
の大きい値に対して指数的というよりむしろ代数的に減少するという意味で「太い」(この動作はこれら周辺分布のSurvivalFunctionを分析することで量的に厳密にすることができる). - 多変量の正の分布(変量ベクトルの各座標が正である分布)の研究は,1970年代にJohnsonとKotzが経済学,心理学,信頼性等の分野でGammaDistribution,BetaDistribution,ParetoDistribution,FRatioDistributionの多変量版を調べたことから流行した.2001年には,多変量正規対数分布は,そのPDFとCDF(累積分布関数)が比較的単純な形をしていることから,多変数の座標成分ごとの正の現象のモデル化の際の魅力的な代替案として導入された.
- RandomVariateを使って,多変量正規対数分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,LogMultinormalDistribution[μ,Σ]] (より簡略な表記では xLogMultinormalDistribution[μ,Σ])を使って,確率変数 x が多変量正規対数分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[LogMultinormalDistribution[μ,Σ],x]およびCDF[LogMultinormalDistribution[μ,Σ],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合が多変量正規対数分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータから多変量パラメトリック正規対数分布を推定することが,FindDistributionParametersを使ってデータを多変量正規対数分布にフィットすることができる.ProbabilityPlotを使って多変量記号正規対数分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って多変量記号正規対数分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された多変量正規対数分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って多変量正規対数分布を含む高次元分布を構築することが,ProductDistributionを使って多変量正規対数分布を含む独立成分分布の結合分布を計算することができる.
- LogMultinormalDistributionは,他の数多くの分布と関連している.LogMultinormalDistributionは,上で説明したように,NormalDistribution,BinormalDistribution,LogNormalDistribution,MultinormalDistributionと関連があり,その対数的動作は,LogLogisticDistribution,LogNormalDistribution,LogGammaDistributionのそれと定性的に類似している.LogMultinormalDistributionの一次元周辺分布のPDFはLogNormalDistributionであるのに対し,多変量周辺分布のそれぞれはLogMultinormalDistributionである.LogMultinormalDistributionは,MultinormalDistribution,BinormalDistribution,LogNormalDistributionの変換(TransformedDistribution)として実現でき,Σが直交行列のときはLogNormalDistributionの積分布(ProductDistribution)としても得られる.多変量正規対数分布は,一変量分布NormalDistributionおよびLogNormalDistributionとの関係から,DavisDistribution,LogLogisticDistribution,ExponentialDistribution,WeibullDistribution,GompertzMakehamDistribution,ExtremeValueDistribution,GammaDistributionとも関係がある.
例題
すべて開くすべて閉じるスコープ (6)
多変量正規対数分布から擬似乱数ベクトルのサンプルを生成する:
一変量周辺分布はLogNormalDistributionに従う:
特性と関係 (7)
LogMultinormalDistributionはMultinormalDistributionの変換である:
LogMultinormalDistributionはBinormalDistributionの変換である:
一次元周辺分布はLogNormalDistributionである:
対角行列を持つ特殊ケースはLogNormalDistributionのProductDistributionである:
LogMultinormalDistributionはLogNormalDistributionと関連している:
LogMultinormalDistributionはGeometricBrownianMotionProcessについてのスライス分布である:
テキスト
Wolfram Research (2012), LogMultinormalDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/LogMultinormalDistribution.html.
CMS
Wolfram Language. 2012. "LogMultinormalDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LogMultinormalDistribution.html.
APA
Wolfram Language. (2012). LogMultinormalDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LogMultinormalDistribution.html