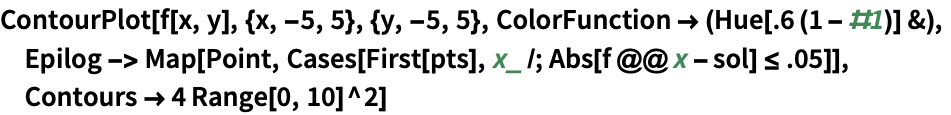NMinValue
✖
NMinValue
詳細とオプション
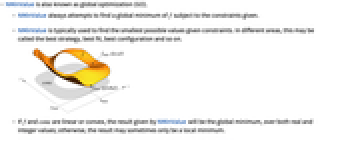

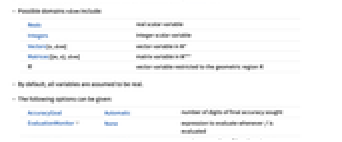

- NMinValueは大域的最適化(GO)としても知られている.
- NMinValueは,与えられた制約条件に従って常に f の最小値を求めようとする.
- NMinValueは,通常,制約が与えられた場合に可能な最小値を求めるために使われる.分野によっては,最適な戦略,最良適合,最適な構成等と呼ばれることがある.
- f と cons が線形または凸のとき,NMinValueが与える結果は実数および整数値の両方の上で最小値になる.それ以外の場合は結果が単に極小値であるかもしれない.
- NMinValueが制約条件を満足できないと判断した場合はInfinityが返される.
- NMinValueは,目的関数 f と制約条件 cons がスカラー変数またはベクトル変数に依存する式で与えられるモデリング言語をサポートする.f と cons は,一般に,非常に効率的な形に解析されるが,f と cons の項が変数の数値に対して数値を与える限りNMinValueはしばしば解を求めることができる.
- 制約条件 cons は以下の論理結合でよい.
-
lhs==rhs 等式 lhs>rhs, lhs≥rhs, lhs<rhs, lhs≤rhs 不等式 (LessEqual, …) lhsrhs, lhsrhs, lhsrhs, lhsrhs ベクトル不等式 (VectorLessEqual, …) {x,y,…}∈rdom 領域指定 - NMinValue[{f,cons},x∈rdom]は,事実上,NMinValue[{f,cons&&x∈rdom},x]に等しい.
- x∈rdomについては,Indexed[x,i]を使って別の座標に言及することができる.
- 次は,使用可能な領域 rdom である.
-
Reals 実数スカラー変数 Integers 整数スカラー変数 Vectors[n,dom] 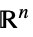 のベクトル変数
のベクトル変数Matrices[{m,n},dom] 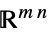 の行列変数
の行列変数ℛ 幾何学領域 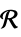 に制限されたベクトル変数
に制限されたベクトル変数 - デフォルトで,変数はすべて実数であるとみなされる.
- 次は,指定可能なオプションである.
-
AccuracyGoal Automatic 目標となる最終確度桁数 EvaluationMonitor None f が評価されたときに常に評価される式 MaxIterations Automatic 使用する最大反復回数 Method Automatic 使用されるメソッド PrecisionGoal Automatic 目標となる最終精度桁数 StepMonitor None ステップを取るたびに常に評価される式 WorkingPrecision MachinePrecision 内部計算に使用する精度 - AccuracyGoalとPrecisionGoalの設定で,最小値の位置の値と最小になったときの関数の値の両方で目標とする桁数を指定する.
- NMinValueは,AccuracyGoalとPrecisionGoalで指定された目標値のどちらかが達成されるまで計算を続ける.
- NMinValueのためのメソッドには2つのクラスがある.最初のクラスは問題の特性を使うので,メソッドが収束する際に求まった最小値は大域的であることが保証される.2番目のクラスは発見的なメソッドで,複数の局所探索を使うことがあるが,一般的には確率論によって調整され,大域的最小値に焦点が当てられる.このメソッドもしばしば大域的な最小値を求めるが,必ずそうするとは保証されない.
- 次は,解に収束する場合に最小値を与えることが保証されているメソッドである.
-
"Convex" 凸法だけを使う "MOSEK" 凸問題用の商用MOSEKライブラリを使う "Gurobi" 凸問題用の商用Gurobiライブラリを使う "Xpress" 凸問題用の商用Xpressライブラリを使う - 次は,発見的な方法である.
-
"NelderMead" Nelder・Meadのシンプレックス法 "DifferentialEvolution" 差分進化を使う "SimulatedAnnealing" 焼きなまし法を使う "RandomSearch" 複数のランダムな初期点から始めて求まった最良の極小値を使う "Couenne" 非凸混合整数非線形問題にCouenneライブラリを使う
例題
すべて開くすべて閉じる例 (4)基本的な使用例
https://wolfram.com/xid/0j47jhg6-faqf4h
https://wolfram.com/xid/0j47jhg6-b6nuhh
https://wolfram.com/xid/0j47jhg6-fcm1i7
https://wolfram.com/xid/0j47jhg6-ewyjra
スコープ (40)標準的な使用例のスコープの概要
基本的な用法 (12)
https://wolfram.com/xid/0j47jhg6-edj208
いくつかの線形不等式制約がVectorGreaterEqualで表現できる:
https://wolfram.com/xid/0j47jhg6-pjuvi
![]() v>=
v>=![]() または\[VectorGreaterEqual]を使ってベクトル不等式の記号を入力する:
または\[VectorGreaterEqual]を使ってベクトル不等式の記号を入力する:
https://wolfram.com/xid/0j47jhg6-ivyhv5
https://wolfram.com/xid/0j47jhg6-ib8bsr
https://wolfram.com/xid/0j47jhg6-lu8fwi
![]() にスレッディングの可能性があるので,不等式
にスレッディングの可能性があるので,不等式 ![]() は
は ![]() とは等しくないかもしれない:
とは等しくないかもしれない:
https://wolfram.com/xid/0j47jhg6-wfe84
https://wolfram.com/xid/0j47jhg6-cdrbb6
![]() での意図しないスレッディングを避けたければInactive[Plus]を使うとよい:
での意図しないスレッディングを避けたければInactive[Plus]を使うとよい:
https://wolfram.com/xid/0j47jhg6-i1qbdu
定数パラメータを持つ方程式を使って ![]() での意図しないスレッディングを回避する:
での意図しないスレッディングを回避する:
https://wolfram.com/xid/0j47jhg6-dd18z3
https://wolfram.com/xid/0j47jhg6-69739j
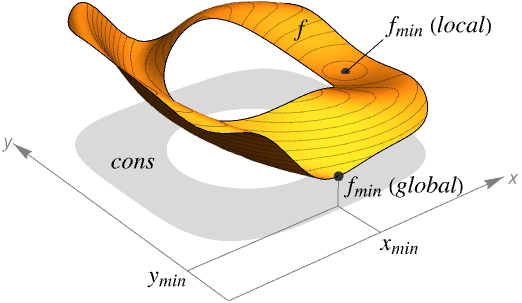
VectorGreaterEqualは"NonNegativeCone"についての錐不等式を表す:
https://wolfram.com/xid/0j47jhg6-c8jcv
円錐の次元を明示的に指定したければ,{"NonNegativeCone",n}を使うとよい:
https://wolfram.com/xid/0j47jhg6-ej00nr
https://wolfram.com/xid/0j47jhg6-bhykun
https://wolfram.com/xid/0j47jhg6-6o2li
"NormCone"で錐不等式を使って制約条件 ![]() を指定する:
を指定する:
https://wolfram.com/xid/0j47jhg6-n3a57
https://wolfram.com/xid/0j47jhg6-jmkzci
https://wolfram.com/xid/0j47jhg6-v9guvz
Indexedを使ってベクトル変数の成分(例:![]() )にアクセスする:
)にアクセスする:
https://wolfram.com/xid/0j47jhg6-p46cfv
ベクトル変数の次元と領域が曖昧なときはVectors[n,dom]を使って指定する:
https://wolfram.com/xid/0j47jhg6-9kphq
https://wolfram.com/xid/0j47jhg6-ev6iib
NonNegativeReals (![]() )を使って非負の制約条件を指定する:
)を使って非負の制約条件を指定する:
https://wolfram.com/xid/0j47jhg6-bsy75
https://wolfram.com/xid/0j47jhg6-uobom
NonPositiveReals (![]() )を使って非正の制約条件を指定する:
)を使って非正の制約条件を指定する:
https://wolfram.com/xid/0j47jhg6-domqhv
https://wolfram.com/xid/0j47jhg6-bim93z
Orという条件を指定することができる:
https://wolfram.com/xid/0j47jhg6-46hoh8
領域制約1 (4)
Integersを使って整数領域の制約を指定する:
https://wolfram.com/xid/0j47jhg6-xi06kw
Vectors[n,Integers]を使ってベクトル変数に整数領域の制約を指定する:
https://wolfram.com/xid/0j47jhg6-df5n5z
NonNegativeIntegers (![]() )を使って非負の整数領域の制約を指定する:
)を使って非負の整数領域の制約を指定する:
https://wolfram.com/xid/0j47jhg6-2eforb
NonPositiveIntegers (![]() )を使って非正の整数領域の制約を指定する:
)を使って非正の整数領域の制約を指定する:
https://wolfram.com/xid/0j47jhg6-f0btvc
領域制約2 (5)
https://wolfram.com/xid/0j47jhg6-q0zuo5
https://wolfram.com/xid/0j47jhg6-2td19x
https://wolfram.com/xid/0j47jhg6-pdj8lj
https://wolfram.com/xid/0j47jhg6-s3co46
https://wolfram.com/xid/0j47jhg6-lo12o0
https://wolfram.com/xid/0j47jhg6-zsebb7
https://wolfram.com/xid/0j47jhg6-fxoyak
https://wolfram.com/xid/0j47jhg6-6vbtl
Circumsphereを使って同じ結果を直接得ることができる:
https://wolfram.com/xid/0j47jhg6-ccn5a7
https://wolfram.com/xid/0j47jhg6-gf8ag3
https://wolfram.com/xid/0j47jhg6-sz8ksq
線形問題 (5)
線形の目的関数と制約条件がある場合は,最小値が見付かるとそれは大域的になる:
https://wolfram.com/xid/0j47jhg6-rx665t
https://wolfram.com/xid/0j47jhg6-7grjvm
Equalを使っていくつかの等式制約を一度に表現する:
https://wolfram.com/xid/0j47jhg6-dkthbi
https://wolfram.com/xid/0j47jhg6-s527v9
VectorLessEqualを使っていくつかのLessEqual不等式制約を一度に表現する:
https://wolfram.com/xid/0j47jhg6-s5e3zm
https://wolfram.com/xid/0j47jhg6-0mtyw2
https://wolfram.com/xid/0j47jhg6-b9pt3y
Intervalを使って変数の境界を指定する:
https://wolfram.com/xid/0j47jhg6-d31yau
凸問題 (7)
"NonNegativeCone"を使って ![]() の形の線形関数を指定する:
の形の線形関数を指定する:
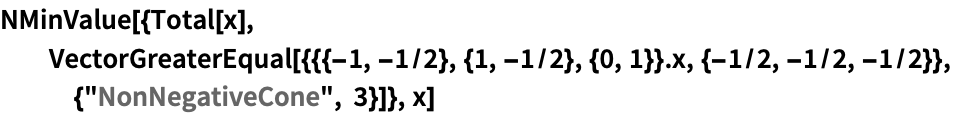
https://wolfram.com/xid/0j47jhg6-hazv2m
https://wolfram.com/xid/0j47jhg6-2347tx
https://wolfram.com/xid/0j47jhg6-16jara
https://wolfram.com/xid/0j47jhg6-d5t5gt
https://wolfram.com/xid/0j47jhg6-q5zkfc
https://wolfram.com/xid/0j47jhg6-pegha4
https://wolfram.com/xid/0j47jhg6-dysqdc
https://wolfram.com/xid/0j47jhg6-ml87f0
https://wolfram.com/xid/0j47jhg6-9j1nn4
凸に変換可能 (4)
縦が最大で横の半分になるようにして,面積が1の長方形の最短外周を求める:
https://wolfram.com/xid/0j47jhg6-kwgi5j
この問題は対数凸問題で,変換{hExp[],wExp[ ]}を行なって対数を取り凸問題にすることで解ける:
https://wolfram.com/xid/0j47jhg6-62ce3
https://wolfram.com/xid/0j47jhg6-forh8e
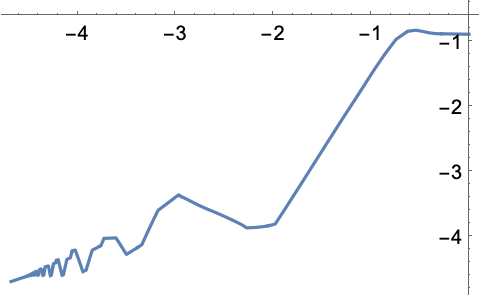
不等式制約とノルム制約に従って擬似凹関数![]() の最小値を求める.目的関数は領域上の非負の関数と非正の関数の積なので,擬似凸関数である:
の最小値を求める.目的関数は領域上の非負の関数と非正の関数の積なので,擬似凸関数である:
https://wolfram.com/xid/0j47jhg6-7xu2gh
擬似凸問題はパラメータ ![]() についてのパラメトリック凸最適化問題として解くことができる:
についてのパラメトリック凸最適化問題として解くことができる:
https://wolfram.com/xid/0j47jhg6-nz65dn
https://wolfram.com/xid/0j47jhg6-36x0u9
https://wolfram.com/xid/0j47jhg6-2eal5r
https://wolfram.com/xid/0j47jhg6-rlvnf0
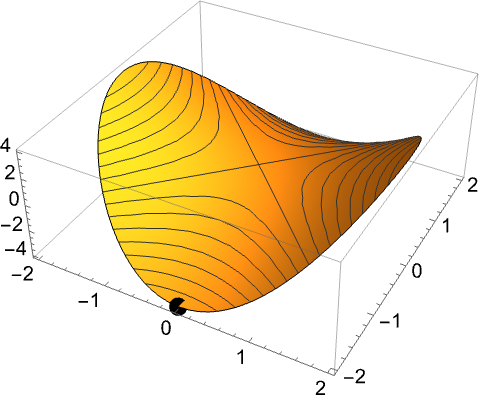
制約条件![]() に従って
に従って ![]() を最小化する.目的関数は凸ではないが,凸関数の差
を最小化する.目的関数は凸ではないが,凸関数の差 ![]() で表すことができる.ただし,
で表すことができる.ただし,![]() と
と ![]() は凸関数である:
は凸関数である:
https://wolfram.com/xid/0j47jhg6-ybo4h2
https://wolfram.com/xid/0j47jhg6-f0dmil
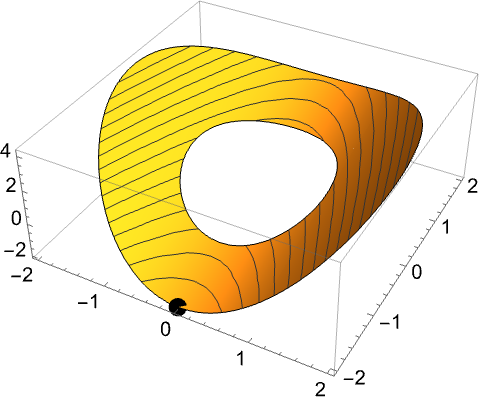
制約条件![]() に従って
に従って ![]() を最小化する.制約条件
を最小化する.制約条件![]() は凸ではないが凸制約の差
は凸ではないが凸制約の差 ![]() で表すことができる.ただし,
で表すことができる.ただし,![]() は凸関数である:
は凸関数である:
https://wolfram.com/xid/0j47jhg6-6vzg6m
https://wolfram.com/xid/0j47jhg6-2fcv6g
オプション (7)各オプションの一般的な値と機能
AccuracyGoalとPrecisionGoal (2)
https://wolfram.com/xid/0j47jhg6-05x0hq
次で,収束基準![]() と
と![]() を強制する.これはデフォルトの機械精度計算では達成できない:
を強制する.これはデフォルトの機械精度計算では達成できない:
https://wolfram.com/xid/0j47jhg6-ykixh5
WorkingPrecisionの設定値を高くするとプロセスが収束するようになる:
https://wolfram.com/xid/0j47jhg6-xk2rz
EvaluationMonitor (1)
Method (2)
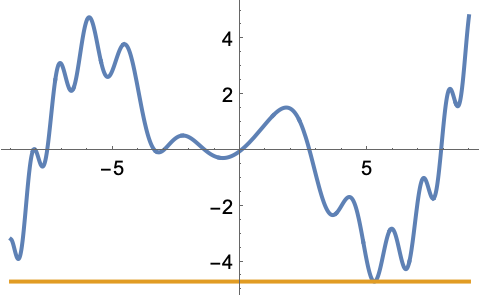
メソッドの中には特定の問題について準最適な結果を返すものがある:

https://wolfram.com/xid/0j47jhg6-ukm3m
この問題については,自動選択されたメソッドが最適な結果を与える:
https://wolfram.com/xid/0j47jhg6-yo3qc8
https://wolfram.com/xid/0j47jhg6-lo8kgo
速度を求めるなら,多くの変数がある問題には"NelderMead"メソッドを使う:

https://wolfram.com/xid/0j47jhg6-cdle4a
StepMonitor (1)
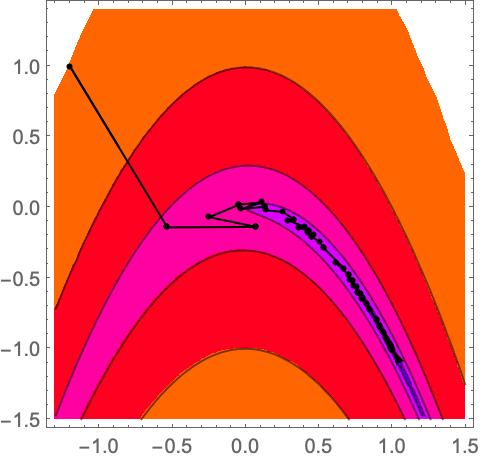
NMinValueが古典的なRosenbrock関数の最小値を求めるのに取るステップ:

https://wolfram.com/xid/0j47jhg6-znwwtn

https://wolfram.com/xid/0j47jhg6-mfc57g
WorkingPrecision (1)
作業精度を![]() にする.デフォルトでAccuracyGoalとPrecisionGoalは
にする.デフォルトでAccuracyGoalとPrecisionGoalは![]() に設定されている:
に設定されている:
https://wolfram.com/xid/0j47jhg6-9rwm4o
アプリケーション (6)この関数で解くことのできる問題の例
幾何学の問題 (3)
![]() と
と ![]() を中心とする半径1の2つの円板間の最短距離を求める.
を中心とする半径1の2つの円板間の最短距離を求める.![]() を円板1の上の点,
を円板1の上の点,![]() を円板2の上の点とする.目的は制約条件
を円板2の上の点とする.目的は制約条件![]() に従って
に従って![]() を最小化することである:
を最小化することである:
https://wolfram.com/xid/0j47jhg6-x0rc5a

https://wolfram.com/xid/0j47jhg6-1xi3kb
https://wolfram.com/xid/0j47jhg6-fmr9yi
https://wolfram.com/xid/0j47jhg6-rvv1lu
包み込む最小の球はBoundingRegionを使って効率的に求めることができる:
https://wolfram.com/xid/0j47jhg6-1dvvd5
https://wolfram.com/xid/0j47jhg6-uhd7v9

指定された半径 ![]() (
(![]() )の重なり合ない
)の重なり合ない ![]() 個の円を収めることができる最小の正方形を求める.円の数と各円の半径を指定する:
個の円を収めることができる最小の正方形を求める.円の数と各円の半径を指定する:
https://wolfram.com/xid/0j47jhg6-m2255i
![]() が円の中心
が円の中心 ![]() なら目的は
なら目的は![]() を最小にすることである.目的は
を最小にすることである.目的は ![]() を最小化することに変換できる.ただし,
を最小化することに変換できる.ただし,![]() である:
である:
https://wolfram.com/xid/0j47jhg6-t7gqfm
https://wolfram.com/xid/0j47jhg6-22nk9i
https://wolfram.com/xid/0j47jhg6-yemsm5
https://wolfram.com/xid/0j47jhg6-fazut5
データフィッティング問題 (1)
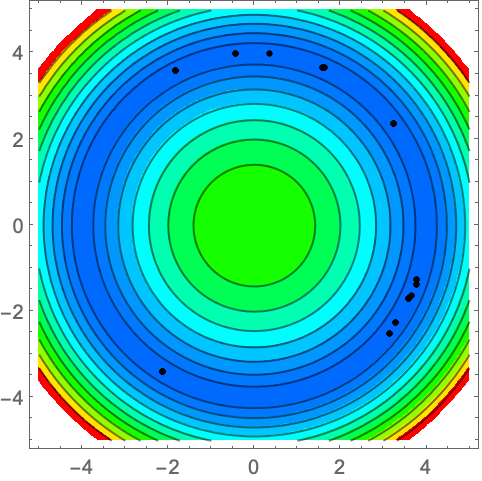
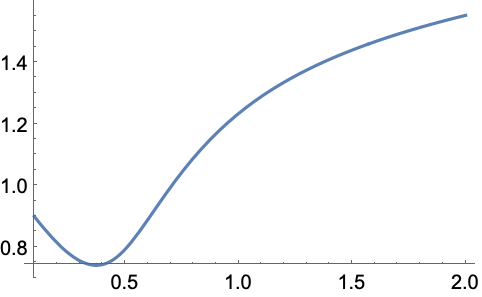
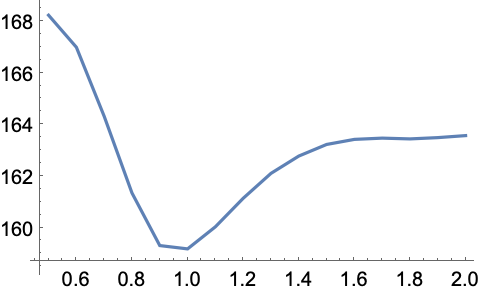
非線形離散データにフィットする ![]() の剰余を最小化するガウスの幅パラメータ
の剰余を最小化するガウスの幅パラメータ ![]() を求める:
を求める:
https://wolfram.com/xid/0j47jhg6-j5yzq8
https://wolfram.com/xid/0j47jhg6-ialjsr
https://wolfram.com/xid/0j47jhg6-lylfvc
https://wolfram.com/xid/0j47jhg6-v27le5
https://wolfram.com/xid/0j47jhg6-gtunrb
https://wolfram.com/xid/0j47jhg6-ccdtpu
反復最適化 (1)
軌跡の最適化 (1)

https://wolfram.com/xid/0j47jhg6-b7tj3j
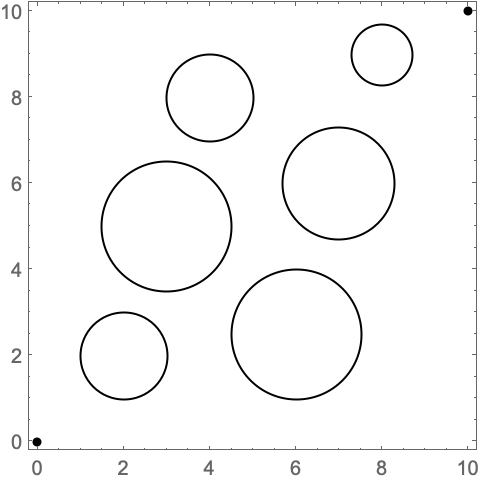
経路は ![]() 個の異なる点で表すことができる.これらの点の間の距離は
個の異なる点で表すことができる.これらの点の間の距離は ![]() 未満でなければならない.ただし,
未満でなければならない.ただし,![]() は最小化する長さである:
は最小化する長さである:
https://wolfram.com/xid/0j47jhg6-518i2b
https://wolfram.com/xid/0j47jhg6-509nls
https://wolfram.com/xid/0j47jhg6-7yhvw9
https://wolfram.com/xid/0j47jhg6-wofkjz
https://wolfram.com/xid/0j47jhg6-7o04by
特性と関係 (8)この関数の特性および他の関数との関係
NMinimizeは最小値と,変数の値を最小にする規則を与える:
https://wolfram.com/xid/0j47jhg6-cq0ogw
NArgMinは最小にする値のリストを与える:
https://wolfram.com/xid/0j47jhg6-dggssc
NMinValueは最小値だけを与える:
https://wolfram.com/xid/0j47jhg6-bsp96p
https://wolfram.com/xid/0j47jhg6-cszj9i
https://wolfram.com/xid/0j47jhg6-0l7ax
凸問題については,ConvexOptimizationを使って追加的な解の特性が得られるかもしれない:
https://wolfram.com/xid/0j47jhg6-dxo13c
https://wolfram.com/xid/0j47jhg6-mlkbfu
https://wolfram.com/xid/0j47jhg6-bpwocb
パラメータがある凸問題について,ParametricConvexOptimizationを使うとParametricFunctionが与えられる:
https://wolfram.com/xid/0j47jhg6-omnnb3
ParametricFunctionはパラメータの値について評価できる:
https://wolfram.com/xid/0j47jhg6-hfii5a
NMinValueを使ってパラメトリック問題についての関数を定義する:

https://wolfram.com/xid/0j47jhg6-ek8e0c

https://wolfram.com/xid/0j47jhg6-hck5xu
ParametricFunctionの導関数も計算できる:
https://wolfram.com/xid/0j47jhg6-fewdju
RobustConvexOptimizationは,パラメータ制約がある凸問題についてはパラメータの可能なすべての値について有効な最適値を求める:

https://wolfram.com/xid/0j47jhg6-dgv79
NMinValueはパラメータの特定の値についてより小さい最小値を求めるかもしれない:
https://wolfram.com/xid/0j47jhg6-cm1b9c
この値を与えるミニマイザは ![]() と
と ![]() の使用可能なすべての値についての制約条件は満足しない:
の使用可能なすべての値についての制約条件は満足しない:
https://wolfram.com/xid/0j47jhg6-gvxgxo
https://wolfram.com/xid/0j47jhg6-dlad5x
パラメータの特定の値について求まった最小値はロバストな最小値以下である:
https://wolfram.com/xid/0j47jhg6-b0rws
https://wolfram.com/xid/0j47jhg6-e1wtev
NMinValueは線形計画問題を解くことができる:
https://wolfram.com/xid/0j47jhg6-mm3mtp
LinearProgrammingを使って行列記法で与えられた同じ問題を解くことができる:
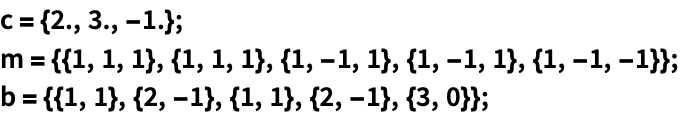
https://wolfram.com/xid/0j47jhg6-i8n5ly
https://wolfram.com/xid/0j47jhg6-b7q2kw
RegionDistanceを使って点から領域までの最短距離を求める:
https://wolfram.com/xid/0j47jhg6-f4g5uc
https://wolfram.com/xid/0j47jhg6-lbd2cp
NMinValueを使って距離を計算する:
https://wolfram.com/xid/0j47jhg6-cl3cvc
RegionBoundsを使って境界ボックスを計算する:
https://wolfram.com/xid/0j47jhg6-eqkvxp
https://wolfram.com/xid/0j47jhg6-jf4d0
NMaxValueとNMinValueを使って同じ境界を計算する:
https://wolfram.com/xid/0j47jhg6-gkt1lb
https://wolfram.com/xid/0j47jhg6-ckoox0
Wolfram Research (2008), NMinValue, Wolfram言語関数, https://reference.wolfram.com/language/ref/NMinValue.html (2024年に更新).テキスト
Wolfram Research (2008), NMinValue, Wolfram言語関数, https://reference.wolfram.com/language/ref/NMinValue.html (2024年に更新).
Wolfram Research (2008), NMinValue, Wolfram言語関数, https://reference.wolfram.com/language/ref/NMinValue.html (2024年に更新).CMS
Wolfram Language. 2008. "NMinValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/NMinValue.html.
Wolfram Language. 2008. "NMinValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/NMinValue.html.APA
Wolfram Language. (2008). NMinValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NMinValue.html
Wolfram Language. (2008). NMinValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NMinValue.htmlBibTeX
@misc{reference.wolfram_2025_nminvalue, author="Wolfram Research", title="{NMinValue}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/NMinValue.html}", note=[Accessed: 23-June-2025
]}BibLaTeX
@online{reference.wolfram_2025_nminvalue, organization={Wolfram Research}, title={NMinValue}, year={2024}, url={https://reference.wolfram.com/language/ref/NMinValue.html}, note=[Accessed: 23-June-2025
]}