NeumannValue

NeumannValue[val,pred]

pred がTrueであるNDSolveおよび関連関数に渡された，領域の境界の部分で指定されたノイマン(Neumann)境界値 val を表す．

詳細

  • NeumannValueは，DSolveやNDSolve等の関数の境界値を指定するために，偏微分方程式内で用いられる．
  • NDSolve[eqns,{u1,u2,…},{x1,x2,…}∈Ω]では，xiは独立変数，ujは従属変数，Ωは境界が ∂Ωの領域である．
  • ノイマン値が指定され得る場所は緑で示される．これは，領域Ωの境界 ∂Ω上に現れるもので，これらの辺を横切って外側の法線に向かう流束を指定する．
  • pred が真である境界 ∂Ω の部分上での流束の指定には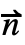，·(c ∇u+α u-γ)=g-q u が成り立つように∇·(-c ∇u-α u+γ)+…=f+NeumannValue[g-q u,pred]が用いられる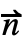．·(c ∇u+α u-γ)=g-q u 中の係数 c，α，γ は，∇·(-c ∇u-α u+γ)+β·∇u+a u=f+NeumannValue[g-q u,pred]で与えられる偏微分方程式を通して陰的に定義される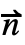． は ∂Ωの外向きの単位法線である．係数 g および q は独立変数{x1,x2,…}のいずれに依存してもよい．
  • 有限要素近似については，偏微分方程式にはテスト関数 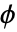が掛けられ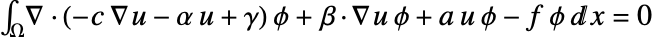，上で積分される．部分的な積分は 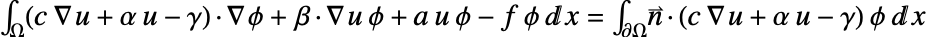を与える．境界積分における被積分関数 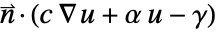はNeumannValue 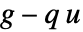で置換され，方程式 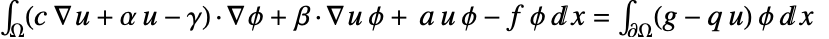を与える．»
  • 有限要素近似では，ノイマン値は，pred がTrueである∂Ω の離散化における各境界要素上の総合的な条件として強制される．境界要素は，1Dでは点，2Dでは辺，3Dでは面である．
  • 境界 ∂Ωの側で境界条件が指定されていない場合は，その部分の上の流束項 ∇·(-c ∇u-α u+γ)+…は f=f+0=f+NeumannValue[0,…]であるとみなされるので，境界条件を全く指定しないことはノイマン0条件を指定することに等しい．
  • 方程式の右辺にある正のNeumannValueは，領域への流束をモデル化する．
  • 述語 pred については，独立変数 x1,…内の方程式および不等式の任意の論理結合を使ってもよい．
  • NeumannValueを使ってノイマンとロビン(Robin)の両方の境界条件を指定することができる．
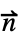  • ·(c ∇u+α u-γ)=0
    		• 自然 (ノイマン0) 条件の指定なし，つまり NeumannValue[0,pred]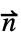
  • ·(c ∇u+α u-γ)=g
    		• ノイマンNeumannValue[g,pred]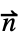
  • ·(c ∇u+α u-γ)=g-q u
    		• ロビン (一般化されたノイマン)NeumannValue[g-q u,pred]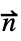
  • ·(c ∇u+α u-γ)=g-h(u)
    		• 一般化された非線形ノイマンNeumannValue[g-h[u],pred]
  • 系については，∇·∑j(-cj∇uj-αjuj+γ)+…f+NeumannValue[g-∑jqjuj]+…は，pred がTrueである領域の部分で条件 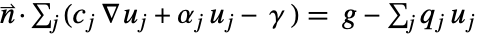が満たされることに相当する．
  • 時間依存方程式については，val と pred の両方が時間に依存してもよい．
  • 偏微分方程式におけるNeumannValueとDerivativeの目的と意味は若干異なる．»
  • 有限要素近似の場合は，NeumannValueは1Dのノード，2Dの辺，3Dの面に作用する．
  • DirichletConditionとNeumannValueは境界の同じ部分に指定されてはならない．
  • NeumannValueの中には境界が重なるものがある．»

例題

すべて開くすべて閉じる

例  (1)

について ，について というディリクレ条件とノイマン条件がある円板上で，ラプラス(Laplace)方程式 を解く：

スコープ  (4)

非線形方程式 を，線分上で，についての一般化されたノイマン条件 と についてのディリクレ条件 で解く：

数値解を解析解で確かめる：

PDEを湾曲した辺上で一般化されたノイマン境界条件で解く：

解を可視化する：

境界の同じ部分で複数のNeumannValueがアクティブにできる：

によじれがある点に注意のこと．より下ではNeumannValueの両方のインスタンスがアクティブであるのに対し，より上では片方のNeumannValueしかアクティブではない．

NeumannValueを使ってDirichletConditionを近似することができる．

DirichletConditionの2つの例とディリクレ値についてのパラメータ を持つ偏微分方程式を解く：

1つのDirichletConditionがスケールされて一般化されたNeumannValueで置換された同じ偏微分方程式を解く：

解の差を調べる：

DirichletConditionをNeumannValueで近似するこのアプローチは，同じ境界範囲に収容されるべきであるディリクレ条件とノイマン値があるときにのみ使われるべきである．

アプリケーション  (12)

1D問題  (2)

ディリクレ境界条件 とロビン境界条件 で，単位長上でを解く：

数値解と解析解を比較する：

ディリクレ境界条件 とロビン境界条件 がある単位長上でを解く：

の値と所定のディリクレ境界条件の値1の差を で比較する：

の値と所定のロビン境界条件の値を で比較する：

これは総合的な条件なので，条件がどの程度満たされるかはメッシュに依存する．より細かいメッシュを使うとよりよい結果が与えられる：

2D問題  (2)

境界で領域を指定する：

領域と境界を示す：

温度が赤と青の境界上で設定され，流束が緑の境界で設定されたラプラス方程式を解く：

ノイマン境界条件を使って領域の対称性を利用することができる．穴のある領域を指定する：

ラプラス演算子を指定する：

内側の境界に ，外側の境界に と，複数のディリクレ条件を設定する：

領域上で方程式を解き，結果を可視化する：

対称な部分領域を指定する：

明示的な条件が設定されていない境界には，ゼロのノイマン条件が想定される：

3D問題  (1)

ノイマン境界条件 で，単位球上の を解く：

時間依存問題  (4)

初期条件と境界条件がある時間依存問題を解く：

反射境界条件がある波動方程式を解く：

吸収境界条件がある波動方程式を解く：

吸収境界条件のある波動方程式を解く．ノイマン値は の一次時間導関数のためである点に注意のこと：

時間によって吸収された波動の量を調べる：

結合系の境界条件  (3)

結合方程式系を指定する：

左辺に2つのディリクレ条件，右辺に2つのノイマン条件がある方程式系を解く：

解をプロットする：

結合微分方程式系を指定する：

ディリクレとノイマンの境界条件を指定し，方程式系を解く：

解をプロットする：

結果を解析解と比較する：

数値解と解析解の間の誤差をプロットする：

ヤング率およびポアソン比で棒の上の平面応力演算子を指定する：

棒は左端を固定されている．右端では，境界荷重が負の 方向に適用されている：

方向の棒の歪みの等高線プロット：

方向の棒の歪みの等高線プロット：

棒の歪みを可視化する：

特性と関係  (1)

このセクションでは領域内に境界条件を設定することが解にどのように影響するかを探ってみる．領域は で に内部境界がある．これについて，，，にノードを持つ有限要素境界メッシュが作成される：

完全メッシュを作成する：

内部教科におけるさまざまな境界条件の動作を示すために拡散係数が の拡散型方程式が選ばれた：

境界条件として，領域の左端と右端に特定の値を設定する：

最初の例では偏微分方程式を0に設定する．つまり，の内部点には他の相互作用はない．これはデフォルトの動作である：

デフォルトの動作は におけるノイマンゼロの値を設定することと同じである：

デフォルト解とノイマンゼロの解の差はゼロである．両者は厳密に等しい解である：

次に，における の特定の値を設定する：

プロットから における従属変数 の値がであることが分かる：

次の実験では，におけるのノイマン値が設定されている．内外がなく法線

    • が向かう方向が不明なのでこれが何を意味するのかははっきりしない．しかし，束の不連続性についての解を計算することはできる：

    以下のプロットはさまざまな内部境界条件を比較している：

    さらに実験を続ける場合は， を設定することで内部物質境界における拡散係数を不連続にすることが考えられる：

    あるいは，境界条件の値を反転することもできる：

    考えられる問題  (4)

    定常偏微分方程式についてもっぱらノイマン境界条件のみを指定すると，結果として一意的ではない解になることがある．場合によっては，系が全く可解ではなくなることもある：

    ロビン境界条件の指定で十分である：

    ディリクレ条件とノイマン条件が について ，について で，吸収係数 のラプラス方程式を矩形上で解く：

    解が右辺のノイマン値と矛盾しないことを確かめる：

    吸収係数 を設定してラプラス方程式を解くと，ノイマン値が になるので注意のこと：

    この解も右辺のノイマン値と矛盾しないことを確かめる：

    2つの解を可視化する：

    境界部分に境界条件を指定しないことは，自然の 境界条件を暗示する：

    これは同じ境界条件である：

    インポートしたメッシュあるいは生成したメッシュが数値的に不正確であることがある．例えば，目的とする領域は四角形であるのに，領域の離散化バージョンに不正確さがあって実際にはになることがある．このような場合に の形式の述語が指定されていれば，は存在しないのでエラーメッセージが生成される．次の構築された例について考える：

    これに対処する方法の一つに，述語を境界として と定式化するものがある．ここで， は境界の厚みである：

    この手法は，数値精度の問題が発生しやすい境界の円形部分のようにより複雑な述語にも使用できる．

    Wolfram Research (2014), NeumannValue, Wolfram言語関数， https://reference.wolfram.com/language/ref/NeumannValue.html （2023年に更新）.

    テキスト

    Wolfram Research (2014), NeumannValue, Wolfram言語関数， https://reference.wolfram.com/language/ref/NeumannValue.html （2023年に更新）.

    CMS

    Wolfram Language. 2014. "NeumannValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/NeumannValue.html.

    APA

    Wolfram Language. (2014). NeumannValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NeumannValue.html

    BibTeX

    @misc{reference.wolfram_2024_neumannvalue, author="Wolfram Research", title="{NeumannValue}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/NeumannValue.html}", note=[Accessed: 22-November-2024 ]}

    BibLaTeX

    @online{reference.wolfram_2024_neumannvalue, organization={Wolfram Research}, title={NeumannValue}, year={2023}, url={https://reference.wolfram.com/language/ref/NeumannValue.html}, note=[Accessed: 22-November-2024 ]}