NicholsPlot
NicholsPlot[lsys]
对于系统 lsys 给出传递函数的 Nichols 图线.
NicholsPlot[lsys,{ωmin,ωmax}]
绘制频率范围为 ωmin 至 ωmax 的图线.
NicholsPlot[expr,{ω,ωmin,ωmax}]
使用变量 ω 绘制 expr.
更多信息和选项


- NicholsPlot 给出 lsys 的传递函数的以幅值为纵坐标、相角为横坐标的图线.
- 系统 lsys 可以是 TransferFunctionModel 或者 StateSpaceModel,包括描述器和延迟系统.
- 对于相应传递函数是
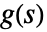 的系统 lsys,可以绘制下列表达式:
的系统 lsys,可以绘制下列表达式: -
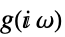
连续时间系统 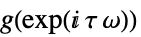
采样时间为 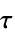 的离散时间系统
的离散时间系统 - NicholsPlot 将变量 ω 视为局部变量,使用 Block.
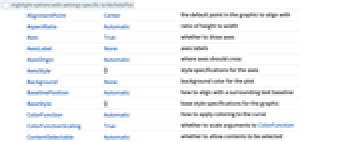
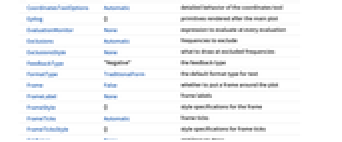
- NicholsPlot 具有和 Graphics 相同的选项,另外有以下变动和添加: [所有选项的列表]
-
Axes True 是否绘制轴 ColorFunction Automatic 如何对曲线着色 ColorFunctionScaling True 是否缩放 ColorFunction 的变量 EvaluationMonitor None 每次计算时,要计算的表达式 Exclusions Automatic 排除的频率 ExclusionsStyle None 在被排除的频率处绘制什么 FeedbackType "Negative" 反馈类型 MaxRecursion Automatic 所允许的递归子划分的最大数目 Mesh Automatic 要绘制多少网格划分点 MeshFunctions {#3&} 如何确定网格点划分的位置 MeshShading None 如何在网格点之间的区域添加阴影 MeshStyle Automatic 网格点划分的样式 NicholsGridLines None 要绘制的 Nichols 网格线 PerformanceGoal $PerformanceGoal 尝试优化哪些方面的性能 PlotLegends None 采样频率的初始数目 PhaseRange Automatic 要包含的幅值和相角值的范围 PlotPoints Automatic 采样频率的初始数目 PlotRange Automatic 要包含的幅值和相角值的范围 PlotRangeClipping True 是否在 PlotRange 处剪切 PlotStyle Automatic 用于指定图线样式的图形指令 PlotTheme $PlotTheme 图线的整体主题 RegionFunction Automatic 如何确定是否包含一个点 SamplingPeriod None 采样周期 ScalingFunctions {"Degree","dB"} 尺度函数 StabilityMargins False 是否显示稳定裕度 StabilityMarginsStyle Automatic 指定稳定裕度的样式的图形指令 WorkingPrecision MachinePrecision 用于内部计算的精度 - ScalingFunctions->{phasescale,magscale} 可用来指定尺度函数.
- 相角标度 phasescale 可以是 "Degree" 或者 "Radian".
- 幅值标度 magscale 可以是 "dB" 或者 "Absolute",它们分别对应于幅值的分贝值和绝对值.
所有选项的列表


范例
打开所有单元关闭所有单元范围 (8)
推广和延伸 (1)
NicholsPlot[TransferFunctionModel[g,var]] 等价于 NicholsPlot[g]:
选项 (28)
ColorFunctionScaling (1)
PlotLegends (4)
Wolfram Research (2010),NicholsPlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/NicholsPlot.html (更新于 2014 年).
文本
Wolfram Research (2010),NicholsPlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/NicholsPlot.html (更新于 2014 年).
CMS
Wolfram 语言. 2010. "NicholsPlot." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/NicholsPlot.html.
APA
Wolfram 语言. (2010). NicholsPlot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/NicholsPlot.html 年