NyquistPlot
NyquistPlot[lsys]
系 sys の伝達関数のナイキスト(Nyquist)線図を生成する.
NyquistPlot[lsys,{ωmin,ωmax}]
ωminから ωmaxまでの周波数領域の線図を与える.
NyquistPlot[expr,{ω,ωmin,ωmax}]
変数 ω を使って expr の線図を与える.
詳細とオプション



- NyquistPlotは,ナイキスト等高線を旋回する際の lsys の伝達関数の複素平面プロットを与える.
- 系 lsys はディスクリプタ系と遅延系を含むTransferFunctionModelまたはStateSpaceModelである.
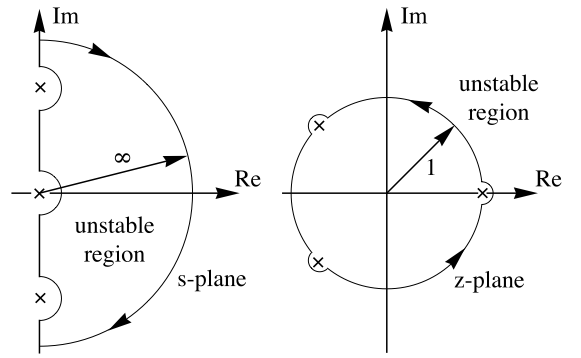
- 連続時間系では,ナイキスト等高線は右半平面全体を包み込み,虚軸上の極を除外する.これは,時計回りに回転する.
- 離散時間系については,ナイキスト等高線は単位円で,単位円上の極を囲む.これは,反時計回りに回転する.
- NyquistPlot上の矢印はナイキスト等高線が回転する方向を表す.
- ナイキスト等高線
- 対応する伝達関数
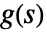 がある系 lsys の場合は次の式がプロットされる.
がある系 lsys の場合は次の式がプロットされる. -
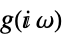
連続時間系 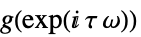
サンプル時間 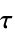 の離散時間系
の離散時間系 - 周波数範囲が指定されていない場合,ナイキスト等高線全体を旋回し,事実上,連続時関係では
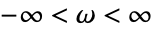 ,離散時間系では
,離散時間系では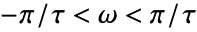 となる.
となる. - NyquistPlotは,事実上Blockを使って,変数 ω を局所的なものとして扱う.
- ナイキスト線図を使って,閉ループ系の不安定な極
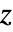 の数を
の数を 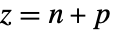 として推測することができる.
として推測することができる.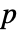 は開ループ系の不安定な極の数,
は開ループ系の不安定な極の数,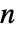 は点
は点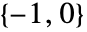 を時計回りに囲い込む回数である. »
を時計回りに囲い込む回数である. » - ナイキスト線図を使って,非線形フィードバック
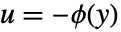 の線形系の大域的指数安定性を推測することができる.ただし,
の線形系の大域的指数安定性を推測することができる.ただし,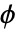 は
は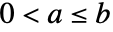 のときにセクターの条件
のときにセクターの条件 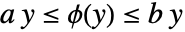 を満たすものとする.閉ループ系は
を満たすものとする.閉ループ系は 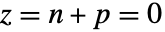 のときは安定している.ただし,
のときは安定している.ただし,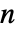 は円板
は円板![TemplateBox[{Disk, paclet:ref/Disk}, RefLink, BaseStyle -> {InlineFormula}][{-(b+a)/(2 a b),0},TemplateBox[{Abs, paclet:ref/Abs}, RefLink, BaseStyle -> {InlineFormula}][(b-a)/(2 a b)]] TemplateBox[{Disk, paclet:ref/Disk}, RefLink, BaseStyle -> {InlineFormula}][{-(b+a)/(2 a b),0},TemplateBox[{Abs, paclet:ref/Abs}, RefLink, BaseStyle -> {InlineFormula}][(b-a)/(2 a b)]]](Files/NyquistPlot.ja/20.png) を時計回りに囲み込む回数であり,
を時計回りに囲み込む回数であり,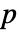 は開ループ不安定極の数である. »
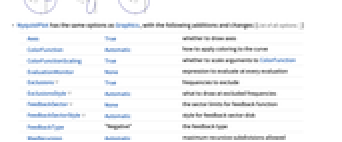
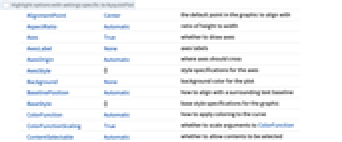
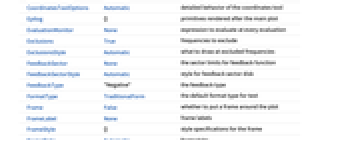
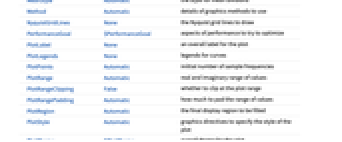
は開ループ不安定極の数である. » - NyquistPlotにはGraphicsと同じオプションに以下の追加・変更を加えたものが使える. [全オプションのリスト]
-
Axes True 座標軸を描くかどうか ColorFunction Automatic 曲線にどのように色付けするか ColorFunctionScaling True ColorFunctionの引数をスケールするかどうか EvaluationMonitor None あらゆる評価で評価する式 Exclusions True 除外する周波数 ExclusionsStyle Automatic 除外された周波数のところに何を描くか FeedbackSector None フィードバック関数のセクターの極限 FeedbackSectorStyle Automatic フィードバックセクター円板のスタイル FeedbackType "Negative" フィードバックタイプ MaxRecursion Automatic 許容する再帰分割の最大数 Mesh Automatic 描画するメッシュ区分の数 MeshFunctions {#3&} メッシュ区分の置き方 MeshShading Automatic メッシュ点の間の領域をどのように陰影付けするか MeshStyle Automatic メッシュ区分のスタイル NyquistGridLines None 描画するナイキスト格子線 PerformanceGoal $PerformanceGoal 最適化を試みるパフォーマンスの局面 PlotLegends None 曲線の凡例 PlotPoints Automatic サンプル周波数の初期数 PlotRange Automatic 値の実数範囲と虚数範囲 PlotStyle Automatic プロットスタイルを指定するグラフィックス指示子 PlotTheme $PlotTheme プロットの全体的なテーマ RegionFunction Automatic ある点を含めるかどうかの決め方 SamplingPeriod None サンプリング周期 StabilityMargins False 安定余裕を示すかどうか StabilityMarginsStyle Automatic 安定余裕のスタイルを指定するグラフィックス指示子 WorkingPrecision MachinePrecision 内部計算で使われる精度 - Exclusions->Trueの設定は,正弦波伝達関数が非連続となる周波数を,共振周波数も含めて除外する.
- Exclusions->{f1,f2,…}は特定の周波数 fiを除外する.
- ExclusionsStyle->s は除外されたそれぞれの点と反対側の点を繋ぐ曲線にスタイル s を使うように指定する.
- 共振周波数における除外箇所に相当する点は無限大において半円で繋がれる.
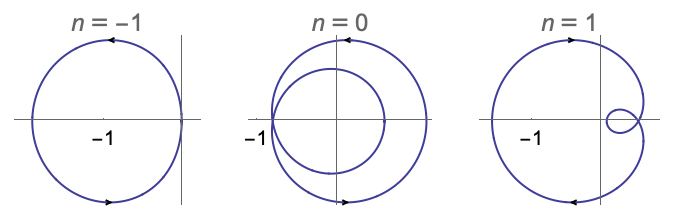
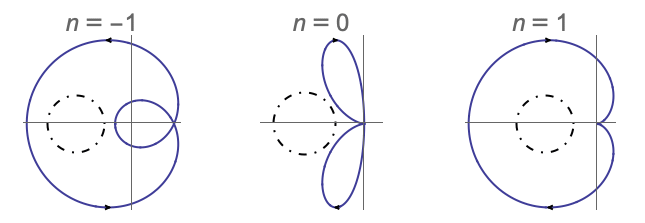
- FeedbackSector->{a,b}は
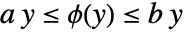 でのフィードバック
でのフィードバック 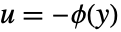 を示す.
を示す.
全オプションのリスト

例題
すべて開くすべて閉じるスコープ (24)
基本的な用法 (11)
線形系の安定性 (7)
非線形系の安定性 (6)
フィードバック ![]() を使う.ただし,
を使う.ただし,![]() であり,円板が囲い込まれていないので
であり,円板が囲い込まれていないので ![]() もまた真である:
もまた真である:
閉ループ系の定期的なフィードバック ![]() のシミュレーションを
のシミュレーションを![]() について行う:
について行う:
以下の安定した系(![]() )には,セクター
)には,セクター![]() におけるフィードバックのための円板の時計回りの囲い込みが1つある(
におけるフィードバックのための円板の時計回りの囲い込みが1つある(![]() ) :
) :
したがって,閉ループ系はそのセクター中の任意のフィードバックについて不安定である:
そのセクター内の任意のフィードバックについて閉ループ系は安定している:
この安定した系はセクター![]() 内にフィードバックがあり,そのNyquistPlotは
内にフィードバックがあり,そのNyquistPlotは![]() の右側にある:
の右側にある:
閉ループはセクター![]() 内の任意のフィードバックについて安定している:
内の任意のフィードバックについて安定している:
NyquistPlotはセクター![]() 内のフィードバックのための円の中にある:
内のフィードバックのための円の中にある:
閉ループはセクター![]() 内の任意のフィードバックについて安定している:
内の任意のフィードバックについて安定している:
フィードバックがセクター![]() の中にある-lsys のNyquistPlotは安定した閉ループ系を示している:
の中にある-lsys のNyquistPlotは安定した閉ループ系を示している:
オプション (26)
Exclusions (5)
FeedbackSector (4)
PlotLegends (4)
PlotRange (2)
テキスト
Wolfram Research (2010), NyquistPlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/NyquistPlot.html (2014年に更新).
CMS
Wolfram Language. 2010. "NyquistPlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/NyquistPlot.html.
APA
Wolfram Language. (2010). NyquistPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NyquistPlot.html