RipleyK

RipleyK[pdata,r]

点データ pdata について半径 r でRipleyの 関数 を推定する．

RipleyK[pproc,r]

点過程 pproc についてを計算する．

RipleyK[bdata,r]

ビン分割データ bdata について を計算する．

RipleyK[pspec]

さまざまな半径 r で繰り返し適用可能な関数 を生成する．

詳細とオプション

  • 積 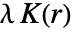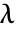（ は平均密度）は，典型的な点からの距離が r 以内の，点自体を数えない点の期待数を与える．
  •     
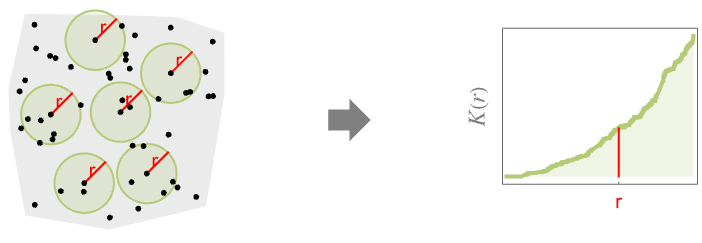
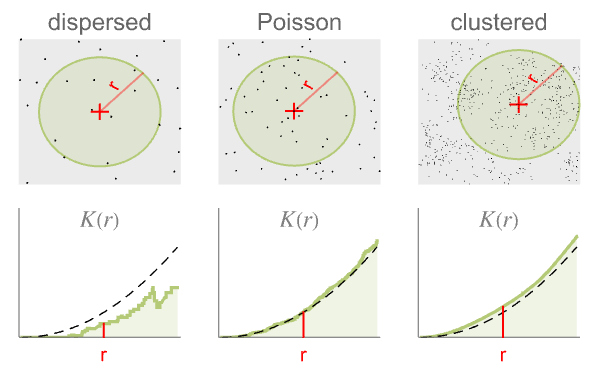
  • RipleyKは，距離 r 内の点集合の空間均質性を測定する．ポアソン(Poisson)点過程と比較すると以下のようになる．
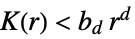
  • ポアソン過程よりも分散している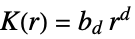
    ポアソン過程のようである，つまり，完全な空間ランダム性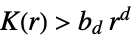
    ポアソン過程よりクラスタ化している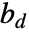
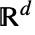  • はにおける単位球の体積である．
  •     
  • 半径 r は，単一の値でも値のリストでもよい．RipleyKは半径 r が指定されていないとPointStatisticFunctionを返す．これを使って 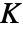関数を繰り返し評価することができる．
  • 点 pdata には次の形がある．
  • {p1,p2,…}点 pi
    GeoPosition[…],GeoPositionXYZ[…],…地理的な点
    SpatialPointData[…]空間点の集合
    {pts,reg}点集合 pts と観測領域 reg
  • 観測領域 reg が与えられていないと，RipleyRassonRegionを使って自動的に領域が計算される．
  • 点過程 pproc には次の形がある．
  • proc点過程 proc
    {proc,reg}点過程 proc と観測領域 reg
  • 観測領域 reg はパラメータフリーでSpatialObservationRegionQでなければならない．
  • ビン分割データ bdata はSpatialBinnedPointDataからのもので，区分定数強化関数によってInhomogeneousPoissonPointProcessとして扱われる．
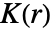  • は pdata について，互いの距離が r 以内の点の重複しないペアを数えることで計算される．
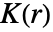  • は pproc について，厳密な公式を使ってあるいはシミュレーションで点データを生成して計算される．
  • 次は，使用可能なオプションである．
  • MethodAutomatic使用するメソッド
    SpatialBoundaryCorrection Automatic使用する境界補正
  • SpatialBoundaryCorrectionには，次の設定を使うことができる．
  • Automatic自動的に決定された境界補正
    None境界補正なし
    "BorderMargin"観測領域として内側余白を使う
    "Ripley"境界までの点の距離に依存する重みを使う

例題

すべて開くすべて閉じる

例  (3)

指定された半径でRipleyの 関数を推定する：

さまざまな距離範囲でRipleyの 関数を推定する：

ListPlotで結果を可視化する：

クラスタ点過程のRipleyの 関数：

指定されたパラメータ値で関数を可視化する：

スコープ  (10)

点データ  (5)

距離0.2におけるRipleyの 関数を推定する：

Ripleyの 関数の経験的推定を指定された距離のリストから取得する：

RipleyKとSpatialPointDataを一緒に使う：

後で使うためにPointStatisticFunctionを作る：

指定された半径での関数の値を求める：

明示的に観測領域を与えることはせずにRipleyの 関数を推定する：

Ripley–Rasson推定器によって生成された観測領域：

距離0.3における 関数を推定する：

RipleyKをGeoPositionと一緒に使う：

点統計関数をプロットする：

点過程  (5)

PoissonPointProcessについてのRipleyの 関数は，強度に依存しない閉じた形を持つ：

関数は に比例する：

指定された次元のクラスタ過程ThomasPointProcessについてのRipleyの 関数：

これは，同じ密度の二次元PoissonPointProcessよりも常に大きい：

3D：

対応するポアソン点過程と比較する：

指定された次元のクラスタ過程MaternPointProcessについてのRipleyの 関数：

3D：

クラスタ過程CauchyPointProcessについてのRipleyの 関数：

クラスタ過程VarianceGammaPointProcessについてのRipleyの 関数：

オプション  (2)

SpatialBoundaryCorrection  (2)

境界補正のないRipleyK推定量は偏っているので，大きい点集合でなければ使うべきではない：

デフォルトメソッドの"BorderMargin"は境界からの距離が の点だけを考慮する：

境界補正法の"Ripley"は点の各ペアに重みを付けて推定量に偏りがないようにする：

さまざまな辺補正法を比較する：

異なる3つのメソッドでRipleyの 関数の値を推定する：

結果を可視化して理論値と比較する：

アプリケーション  (6)

Ripleyの 関数は距離において累積的であり，したがって単調増加である：

完全な空間的ランダム性についてのRipleyの 関数：

Ripleyの 関数をいくつかの次元で計算する：

結果を可視化する：

ハードコア点過程の点はハードコア半径 よりも近くてはならない：

Ripleyの 過程の値を推定する：

結果を可視化する：

3つのサンプルのハードコア半径の推定値を求める：

クラスタデータについてのRipleyの 関数は完全に空間的にランダムなデータよりも高い．次はクラスタ過程からのサンプルである：

同じ強度のポアソン点過程から比較参照用のサンプルを生成する：

RipleyK関数を比較する：

2000年から2015年までにカリフォルニアで発生したマグニチュード4以上の地震：

地震の発生場所を抽出する：

RipleyKを計算する：

データの平均点密度：

データ中の典型的な点から半径2マイルで発生した地震の期待数：

Ripleyの 関数を使ってPairCorrelationGを推定する：

データからの対相関：

Ripleyの 関数を計算する：

対相関を推定する：

推定値とデータから計算された対相関を比較する：

特性と関係  (1)

BesagLはRipleyKの安定した分散である．，ただし，はRipleyの 関数， は空間次元，はにおける単位球体の体積である：

両方の統計を計算する：

式を確認する：

考えられる問題  (1)

境界補正がある経験的RipleyKは増加しないかもしれない（特に小さい集合に対しては）：

境界補正がないRipleyKは増加する：

Wolfram Research (2020), RipleyK, Wolfram言語関数， https://reference.wolfram.com/language/ref/RipleyK.html.

テキスト

Wolfram Research (2020), RipleyK, Wolfram言語関数， https://reference.wolfram.com/language/ref/RipleyK.html.

CMS

Wolfram Language. 2020. "RipleyK." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RipleyK.html.

APA

Wolfram Language. (2020). RipleyK. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RipleyK.html

BibTeX

@misc{reference.wolfram_2024_ripleyk, author="Wolfram Research", title="{RipleyK}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/RipleyK.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ripleyk, organization={Wolfram Research}, title={RipleyK}, year={2020}, url={https://reference.wolfram.com/language/ref/RipleyK.html}, note=[Accessed: 18-November-2024 ]}