RipleyK
RipleyK[pdata,r]
估计点数据 pdata 在半径 r 内的 Ripley's ![]() 函数
函数 ![]() .
.
RipleyK[pproc,r]
计算点过程 pproc 的![]() .
.
RipleyK[bdata,r]
计算分组过的数据 bdata 的 ![]() .
.
RipleyK[pspec]
生成可重复应用于不同半径 r 的函数 ![]() .
.
更多信息和选项



- 积
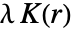 ,其中
,其中 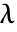 为平均密度,给出期望位于点 r 距离范围内的点数,不计算点本身.
为平均密度,给出期望位于点 r 距离范围内的点数,不计算点本身. -
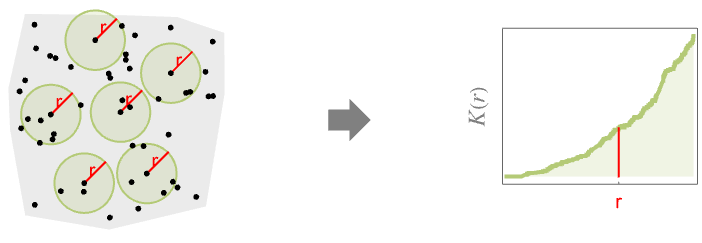
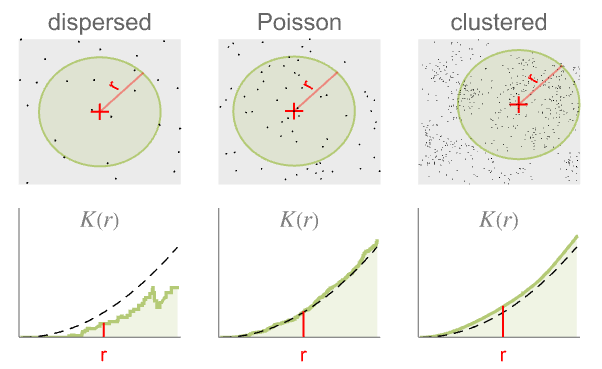
- RipleyK 测量半径 r 内的点的空间均匀性. 与泊松点过程相比的结果为:
-
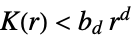
比泊松点过程更分散 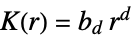
与泊松点过程相似,即具有完全空间随机性 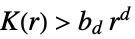
比泊松点过程聚类性更强 - 下面,
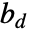 是
是 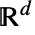 中单位球体的体积.
中单位球体的体积. -
- 半径 r 可以是单个值或值的列表. 如果没有指定 r,RipleyK 会返回一个 PointStatisticFunction,可用其重复计算
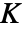 函数.
函数. - 可用以下形式给出点 pdata:
-
{p1,p2,…} 点 pi GeoPosition[…],GeoPositionXYZ[…],… 地理点 SpatialPointData[…] 空间点集 {pts,reg} 点集 pts 和观察区域 reg - 如果没有给出观察区域 reg,则用 RipleyRassonRegion 自动计算区域.
- 可用以下形式给出点过程 pproc:
-
proc 点过程 proc {proc,reg} 点过程 proc 和观察区域 reg - 观察区域 reg 不应含有参数且 SpatialObservationRegionQ 的结果为真.
- 已分组数据 bdata 来自 SpatialBinnedPointData,且被视为是具有分段恒定强度函数的 InhomogeneousPoissonPointProcess.
- 对于 pdata,通过统计彼此之间的距离 r 内有多少对不同的点来计算
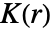 .
. - 对于 pproc,通过使用精确公式或通过仿真生成点数据来计算
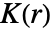 .
. - 可给出以下选项:
-
Method Automatic 使用什么方法 SpatialBoundaryCorrection Automatic 使用什么样的边界校正 - 对于 SpatialBoundaryCorrection,可使用以下设置:
-
Automatic 自动确定边界校正 None 不进行边界校正 "BorderMargin" 对于观察区域使用内边界 "Ripley" 根据到边界的距离进行加权
范例
打开所有单元关闭所有单元基本范例 (3)
范围 (10)
点数据 (5)
点过程 (5)
PoissonPointProcess 的 Ripley's ![]() 函数有不依赖于强度的解析形式:
函数有不依赖于强度的解析形式:
指定维度的聚类点过程 ThomasPointProcess 的 Ripley's ![]() 函数:
函数:
总是大于同样密度的二维的 PoissonPointProcess:
指定维度的聚类点过程 MaternPointProcess 的 Ripley's ![]() 函数:
函数:
聚类过程 CauchyPointProcess 的 Ripley's ![]() 函数:
函数:
聚类过程 VarianceGammaPointProcess 的 Ripley's ![]() 函数:
函数:
选项 (2)
SpatialBoundaryCorrection (2)
不包含边界校正的 RipleyK 估计器存在偏差,除非是处理较大的点集,否则不应使用:
默认方法 "BorderMargin" 仅考虑距边界 ![]() 的点:
的点:
应用 (6)
聚类数据的 Ripley's ![]() 比完全空间随机的数据的 Ripley's
比完全空间随机的数据的 Ripley's ![]() 要大. 聚类过程的样本:
要大. 聚类过程的样本:
比较 RipleyK 函数:
比较 RipleyK:
用 Ripley's ![]() 函数估计 PairCorrelationG:
函数估计 PairCorrelationG:
文本
Wolfram Research (2020),RipleyK,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RipleyK.html.
CMS
Wolfram 语言. 2020. "RipleyK." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/RipleyK.html.
APA
Wolfram 语言. (2020). RipleyK. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RipleyK.html 年