UniformDistribution
UniformDistribution
UniformDistribution[{min,max}]
表示一个分布值位于 min 和 max 之间的连续均匀统计分布.
表示一个分布值位于 0 和 1 之间的均匀分布.
UniformDistribution[{{xmin,xmax},{ymin,ymax},…}]
表示一个在区域 {{xmin,xmax},{ymin,ymax},…} 中的多元均匀分布.
表示在标准 n 维单位超立方体下的多变量均匀分布.
更多信息
- UniformDistribution 亦称矩形分布.
- x 的概率密度值是一个均匀分布，min≤x≤max 时为常数， x<min 或 x>max 时为 0. »
- UniformDistribution 规定 min 和 max 可以是任意满足 min<max 的实数.
- UniformDistribution 允许 min 和 max 为任意单位量纲相同的量. »
- UniformDistribution 可与 Mean、CDF 和 RandomVariate 等函数一起使用. »
背景
- UniformDistribution[{a,b}] 表示随机变量在区间
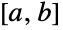上等概率取值的统计分布，被称为均匀分布（有时候又被称为矩形分布）. 因此，均匀分布完全被其定义域的端点参数化并且它的概率密度函数在区间 
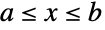上是个常数. 可用 UniformDistribution[] 返回的标准均匀分布在区间 
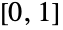上取值. 均匀分布也可以推广到多变量情形，每个变量都在其定义域上均匀分布. - 逆变换方法是均匀分布的一个重要应用，它可以从任意分布中取样，只要把目标随机变量的累积分布函数的反函数作用到均匀分布的随机变量上即可. 另一个重要的性质是当用某连续分布的 p-值作为检验分布来检验一个零假设时，若零假设为真则 p-值是标准均匀分布的.
- RandomVariate 可被用于给出均匀分布的一个或多个机器精度或任意精度（后者可用 WorkingPrecision 选项指定）的伪随机变量. Distributed[x,UniformDistribution[{a,b}]]，更简洁的写法是 xUniformDistribution[{a,b}]，可被用于声明随机变量 x 是均匀分布的. 这样一个声明之后可用在如 Probability、NProbability、Expectation 以及 NExpectation 这样的函数中.
- 概率密度函数和累积分布函数可用 PDF[UniformDistribution[{a,b}],x] 和 CDF[UniformDistribution[{a,b}],x] 求得. 平均数、中位数、方差、原点矩及中心矩可分别用 Mean、Median、Variance、Moment 和 CentralMoment 计算.
- DistributionFitTest 可被用于测试给定的数据集是否与均匀分布一致，EstimatedDistribution 可被用于根据给定数据估算均匀参数化分布，而 FindDistributionParameters 可拟合数据和均匀分布. ProbabilityPlot 可被用于生成给定数据的 CDF 相对于符号均匀分布的 CDF 的图线，而 QuantilePlot 可被用于生成给定数据的分位数相对于符号均匀分布的分位数的图线.
- TransformedDistribution 可被用于表示转换的均匀分布，CensoredDistribution 可被用于表示删截后位于上限值和下限值之间的值分布，而 TruncatedDistribution 可被用于表示截断后位于上限值和下限值之间的值分布. CopulaDistribution 可被用于建立包含了均匀分布的高维分布，而 ProductDistribution 可被用于计算包括均匀分布在内的，若干个独立分量的联合分布.
- 均匀分布与许多其它分布相关. 例如，UniformDistribution[] 是 BetaDistribution 和 PowerDistribution 的特例，意思是说（在包括对端点
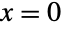和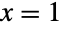 
取模的情况下），PDF[UniformDistribution[],x] 同时等于 PDF[BetaDistribution[1,1],x] 和 PDF[PowerDistribution[1,1],x]. 离散均匀分布由 DiscreteUniformDistribution 给出，而 UniformSumDistribution 把均匀分布推广为 
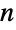个均匀分布的随机变量之和的分布. 两个独立同分布的均匀分布之和是一个对称的 TriangularDistribution. 若 
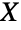是标准均匀分布，则 
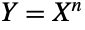是参数为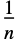 
和 1 的 BetaDistribution. 标准均匀分布的独立同分布的样本 
的 
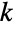
阶统计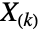 
（可用 OrderDistribution[{UniformDistribution[],n},k] 得到）的概率分布是 BetaDistribution[k,1-k+n]，
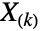对应的期望值（可用 Expectation[x,xBetaDistribution[k,1-k+n]] 计算）是 
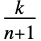. 其它密切相关的分布包括 VonMisesDistribution、LogisticDistribution、WeibullDistribution、LaplaceDistribution、BatesDistribution 和 ChiSquareDistribution.
范例
打开所有单元 关闭所有单元基本范例 (4)
Plot[Table[PDF[UniformDistribution[{0, max}], x], {max, {1, 2, 4}}]//Evaluate, {x, 0, 5}, PlotRange -> All, Filling -> Axis]PDF[UniformDistribution[{min, max}], x]Plot[Table[CDF[UniformDistribution[{0, max}], x], {max, {1, 2, 4}}]//Evaluate, {x, 0, 5}, Filling -> Axis, Exclusions -> None]CDF[UniformDistribution[{min, max}], x]Mean[UniformDistribution[{min, max}]]Variance[UniformDistribution[{min, max}]]Median[UniformDistribution[{min, max}]]范围 (15)
Table[Plot3D[PDF[UniformDistribution[{{1, 3}, {1, d}}], {x, y}], {x, 0, 4}, {y, 0, d + 1}, AxesLabel -> Automatic, PlotLabel -> Row[{"d = ", d}]], {d, {3, 5}}]PDF[UniformDistribution[{{a, b}, {c, d}}], {x, y}]Table[Plot3D[CDF[UniformDistribution[{{1, 3}, {1, d}}], {x, y}], {x, 0, 4}, {y, 0, d + 1}, Exclusions -> None, AxesLabel -> Automatic, PlotLabel -> Row[{"d = ", d}]], {d, {3, 5}}]CDF[UniformDistribution[{{a, b}, {c, d}}], {x, y}]Mean[UniformDistribution[{{a, b}, {c, d}}]]Variance[UniformDistribution[{{a, b}, {c, d}}]]Covariance[UniformDistribution[{{a, b}, {c, d}}]]//MatrixFormdata = RandomVariate[UniformDistribution[{1, 3}], 10 ^ 4];Show[
Histogram[data, 20, "PDF"],
Plot[PDF[UniformDistribution[{1, 3}], x], {x, 0, 3}, PlotStyle -> Thick]]sample = RandomVariate[UniformDistribution[{1, 4}], 10 ^ 3];edist = EstimatedDistribution[sample, UniformDistribution[{min, max}]]Show[Histogram[sample, Automatic, "PDF"], Plot[PDF[edist, x], {x, 1, 4}, PlotStyle -> Thick]]sample = RandomVariate[UniformDistribution[{{0, 3}, {1, 4}}], 10 ^ 3];edist = EstimatedDistribution[sample, UniformDistribution[{{a, b}, {c, d}}]]Skewness[UniformDistribution[{min, max}]]Skewness[UniformDistribution[{{a, b}, {c, d}, {e, f}}]]Kurtosis[UniformDistribution[{min, max}]]Kurtosis[UniformDistribution[{{a, b}, {c, d}, {e, f}}]]Correlation[UniformDistribution[{{a, b}, {c, d}, {e, f}}]]//MatrixFormFormulaGrid[list_, type_] := Grid[...]FormulaGrid[Table[Moment[UniformDistribution[{min, max}], k], {k, 5}], M]Moment[UniformDistribution[{min, max}], r]FormulaGrid[Table[CentralMoment[UniformDistribution[{min, max}], k], {k, 5}], CM]CentralMoment[UniformDistribution[{min, max}], r]FormulaGrid[Table[FactorialMoment[UniformDistribution[{min, max}], k], {k, 5}], FM]FormulaGrid[Table[Cumulant[UniformDistribution[{min, max}], k], {k, 5}], C]Cumulant[UniformDistribution[{min, max}], r]FormulaGrid[list_, type_] := Grid[...]FormulaGrid[Table[Moment[UniformDistribution[{{a, b}, {c, d}}], {2, k}]//Simplify, {k, 1, 3}], M]Moment[UniformDistribution[{{a, b}, {c, d}}], {r, k}]FormulaGrid[Table[CentralMoment[UniformDistribution[{{a, b}, {c, d}}], {2, k}]//FullSimplify, {k, 1, 3}], CM]CentralMoment[UniformDistribution[{{a, b}, {c, d}}], {r, k}]FormulaGrid[Table[FactorialMoment[UniformDistribution[{{a, b}, {c, d}}], {2, k}]//Simplify, {k, 1, 3}], FM]FormulaGrid[Table[Cumulant[UniformDistribution[{{a, b}, {c, d}}], {2, k}]//Simplify, {k, 0, 3}], C]Cumulant[UniformDistribution[{{a, b}, {c, d}}], {r, k}]Plot[Table[HazardFunction[UniformDistribution[{0, max}], x], {max, {1, 3, 4}}]//Evaluate, {x, 0, 4}, Filling -> Axis]HazardFunction[UniformDistribution[{min, max}], x]Table[Plot3D[HazardFunction[UniformDistribution[{{1, 3}, {1, d}}], {x, y}], {x, 1, 3}, {y, 1, d}, AxesLabel -> Automatic, PlotLabel -> Row[{"d = ", d}]], {d, {3, 5}}]HazardFunction[UniformDistribution[{{a, b}, {c, d}}], {x, y}]Plot[Table[Quantile[UniformDistribution[{0, max}], q], {max, {1, 3, 5}}]//Evaluate, {q, 0, 1}, Filling -> Axis]Quantile[UniformDistribution[{min, max}], q]𝒟 = UniformDistribution[{{a, b}, {c, d}, {e, f}}];MarginalDistribution[𝒟, 1]MarginalDistribution[𝒟, {2, 3}]在参数中对 Quantity 一致的使用产生了 QuantityDistribution:
sideLength𝒟 = UniformDistribution[{Quantity[1, "Meters"], Quantity[3, "Meters"]}]Mean[TransformedDistribution[w h, {wsideLength𝒟, hsideLength𝒟}]]Quantity 参数只需要在每一维中保持一致：
heightWeight𝒟 = UniformDistribution[{{Quantity[160, "Centimeters"], Quantity[190, "Centimeters"]}, {Quantity[70, "Kilograms"], Quantity[120, "Kilograms"]}}]Mean[heightWeight𝒟]应用 (12)
Probability[x < Mean[UniformDistribution[{min, max}]], xUniformDistribution[{min, max}]]//Simplify
Probability[Abs[Mod[Subscript[θ, 1] - Subscript[θ, 2], 2Pi]] < Pi / 4, {Subscript[θ, 1]UniformDistribution[{0, 2π}], Subscript[θ, 2]UniformDistribution[{0, 2π}]}]Graphics[Point[Table[{Cos[θ], Sin[θ]}, {θ, RandomVariate[UniformDistribution[{0, 2π}], 100]}]]]invcdf[q_] = InverseCDF[ExtremeValueDistribution[2, 3], q]data = invcdf /@ RandomVariate[UniformDistribution[{0, 1}], 10 ^ 4];Show[Histogram[data, 20, "PDF"], Plot[PDF[ExtremeValueDistribution[2, 3], x], {x, -5, 30}, PlotStyle -> Thick]]喷泉的喷嘴以速度 
和角度 
喷水，以相等的概率在 
和 
之间变化. 求水触及地面的期望水平距离：
Expectation[v ^ 2 2 Sin[α]Cos[α] / g, α UniformDistribution[{π / 6, π / 3}]]len𝒟 = UniformDistribution[{Quantity[10, "Meters"], Quantity[20, "Meters"]}]Mean[TransformedDistribution[w h, {wlen𝒟, hlen𝒟}]]Mean[TransformedDistribution[w ^ 2, wlen𝒟]]//N正弦信号的相位角 
在 
到 
之间均匀分布. 求 
位于 
和 
之间的概率：
𝒟 = UniformDistribution[{0, 2π}];Probability[π / 4 ≤ θ ≤ π / 2, θ𝒟]
Probability[θ ≤ π / 3, θ𝒟]
Mean[𝒟]
sd = StandardDeviation[𝒟]Probability[Mean[𝒟] - sd ≤ θ ≤ Mean[𝒟] + sd, θ𝒟]两列火车到达车站的时间互相独立并停留10分钟. 如果到达时间服从均匀分布，求两列火车在一小时内在该站相遇的概率：
trains𝒟 = UniformDistribution[{Quantity[{0, 60}, "Minutes"], Quantity[{0, 60}, "Minutes"]}]Probability[Abs[x - y] < Quantity[10, "Minutes"], {x, y}trains𝒟]RegionPlot[Abs[x - y] < 10, {x, 0, 60}, {y, 0, 60}, FrameLabel -> {"train 1", "train 2"}]轴的生产与轴承座的生产无关. 轴的直径 
在 
上服从均匀分布，轴承座内径 
在 
上服从均匀分布. 已知两直径之间的最优差值至多为 
，求轴能够装入轴承座的概率：
NProbability[dh - Quantity[0.5, "Millimeters"] < ds < dh, dsUniformDistribution[{Quantity[48.5, "Millimeters"], Quantity[50.5, "Millimeters"]}] && dhUniformDistribution[{Quantity[49, "Millimeters"], Quantity[51, "Millimeters"]}]]RegionPlot[{x^2 + y^2 < (50.5 / 2)^2, (49 / 2)^2 < x^2 + y^2}, {x, 0, 50.5 / 2}, {y, 0, 50.5 / 2}, PlotPoints -> 50]sf = SurvivalFunction[UniformDistribution[{0, max}], t]HazardFunction[UniformDistribution[{0, max}], t]rs = SurvivalFunction[UniformDistribution[{0, max1}], t]SurvivalFunction[UniformDistribution[{0, max2}], t]//PiecewiseExpandrp = 1 - (1 - SurvivalFunction[UniformDistribution[{0, max1}], t])(1 - SurvivalFunction[UniformDistribution[{0, max2}], t])//PiecewiseExpand当 max1=10 且 max2=15 时，比较两个系统的可靠性：
Block[{max1 = 10, max2 = 15}, Plot[{rs, rp}, {t, 0, 15}, PlotLegends -> {"in series", "in parallel"}]]CompareHistogram3D[dist_, {xmin_, xmax_, dx_}, {ymin_, ymax_, dy_}, df_ : PDF, opts___ ? OptionQ] :=
Module[{hist, dplot},
hist = Histogram3D[RandomVariate[dist, 10 ^ 4], {{xmin, xmax, dx}, {ymin, ymax, dy}}, ToString[df], PlotRange -> {{xmin, xmax}, {ymin, ymax}, All}, ChartBaseStyle -> Opacity[0.5]];
dplot = Plot3D[df[dist, {x, y}], {x, xmin, xmax}, {y, ymin, ymax}, Mesh -> {Range[xmin, xmax, dx], Range[ymin, ymax, dy]}, PlotRange -> All, MeshStyle -> Gray, PlotStyle -> Hue[.15, .7, .8]];
Show[hist, dplot]
];𝒟 = UniformDistribution[{{ 2, 4}, {1, 3}}];CompareHistogram3D[𝒟, {1, 5, .5}, {0, 4, .5}, PDF]CompareHistogram3D[𝒟, {1, 5, .5}, {0, 4, .5}, CDF]
𝒫 = WhiteNoiseProcess[UniformDistribution[{-1, 1}]];data = RandomFunction[𝒫, {0, 70}];ListPlot[data, Filling -> Axis]属性和关系 (21)
TransformedDistribution[a * u + b, uUniformDistribution[{min, max}], Assumptions -> a > 0]TransformedDistribution[-3.4 u + b, uUniformDistribution[{min, max}]]TruncatedDistribution[{a, b}, UniformDistribution[{min, max}]]
个均匀分布变量的和服从 UniformSumDistribution：
CharacteristicFunction[UniformDistribution[{min, max}], t] ^ nCharacteristicFunction[UniformSumDistribution[n, {min, max}], t]% - %%TransformedDistribution[(u + v + w), {u, v, w}ProductDistribution[{UniformDistribution[{0, 1}], 3}]]
个均匀分布变量的均值服从 BatesDistribution：
(CharacteristicFunction[UniformDistribution[{0, 1}], t / n]) ^ nCharacteristicFunction[BatesDistribution[n], t]% - %%𝒟 = TransformedDistribution[(u + v + w) / 3, {u, v, w}UniformDistribution[3]];PDF[𝒟, x]PDF[BatesDistribution[3], x]FullSimplify[% - %%]DiscreteUniformDistribution 是离散形式的 UniformDistribution：
PDF[UniformDistribution[{min, max}], x]PDF[DiscreteUniformDistribution[{min, max}], x]两个均匀随机变量的均值，是一个 TriangularDistribution：
𝒟 = Assuming[{a > 0}, TransformedDistribution[(u + v) / 2, {u, v}ProductDistribution[{UniformDistribution[{0, a}], 2}]]];Block[{a = 2}, Show[Histogram[RandomVariate[𝒟, 10 ^ 4], 20, "PDF"], Plot[PDF[TriangularDistribution[{0, a}], x], {x, 0, a}, PlotStyle -> Thick]]]PDF[𝒟, x]//FullSimplify[#, a > 0]&PDF[TriangularDistribution[{0, a}], x]FullSimplify[% - %%, a > 0 && 0 < x < a]CharacteristicFunction[UniformDistribution[{min, max}], t / 2] ^ 2CharacteristicFunction[TriangularDistribution[{min, max}], t]%% - %//FullSimplifyExponentialDistribution 是 
的极限分布，其中 
服从均匀分布：
mindist = OrderDistribution[{UniformDistribution[{0, 1}], n}, 1];CDF[mindist, x / n]Limit[CDF[mindist, x / n], n -> ∞]CDF[ExponentialDistribution[1], x]% - %%//FullSimplifyBetaDistribution 是均匀分布变量的次序分布：
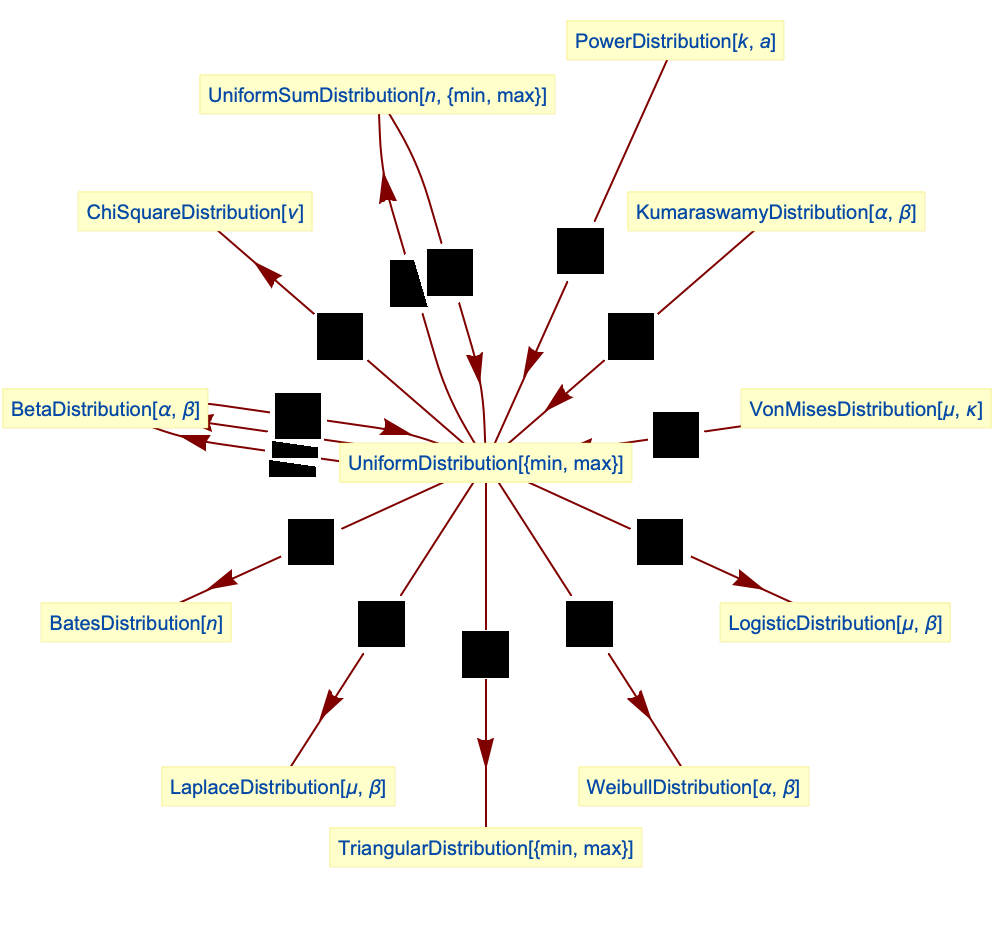
OrderDistribution[{UniformDistribution[{0, 1}], n}, k]BetaDistribution 是 UniformDistribution 的一种变换：
TransformedDistribution[u ^ a, uUniformDistribution[]]ArcSinDistribution 是 UniformDistribution 的一种变换：
TransformedDistribution[Sin[x], xUniformDistribution[{-π, π}]]TransformedDistribution[Cos[x], xUniformDistribution[{-π, π}]]UniformDistribution 是 BetaDistribution 的一种变换：
TransformedDistribution[u ^ a, uBetaDistribution[a, 1]]UniformDistribution 是 KumaraswamyDistribution 的一种变换：
TransformedDistribution[u ^ a, uKumaraswamyDistribution[a, 1]]UniformDistribution 是 PowerDistribution 的一种变换：
TransformedDistribution[u ^ a, uPowerDistribution[1, a]]ChiSquareDistribution 是 UniformDistribution 的一个变换：
𝒟 = TransformedDistribution[-2 Log[u], uUniformDistribution[{0, 1}]];PDF[𝒟, x]//FullSimplify[#, x∈Reals]&PDF[ChiSquareDistribution[2], x]FullSimplify[% - %%, x > 0]LaplaceDistribution 是 UniformDistribution 的一个变换：
TransformedDistribution[Log[u / v], {u, v}ProductDistribution[{UniformDistribution[{0, a}], 2}], Assumptions -> a > 0]LogisticDistribution 是 UniformDistribution 的一个变换：
𝒟 = TransformedDistribution[μ + β(Log[u] - Log[1 - u]), uUniformDistribution[{0, 1}]] ;PDF[𝒟, x]//Simplify[#, β > 0]&PDF[LogisticDistribution[μ, β], x]Simplify[% - %%]UniformDistribution 是 VonMisesDistribution 的一个特例：
PDF[VonMisesDistribution[μ, 0], x]PDF[UniformDistribution[{μ - π, μ + π}], x]% - %%//SimplifyWeibullDistribution 是 UniformDistribution 的一个变换：
𝒟 = TransformedDistribution[β (-Log[1 - u]) ^ (1 / α), uUniformDistribution[{0, 1}]];Block[{α = 3, β = 0.6}, Show[Histogram[RandomVariate[𝒟, 10 ^ 4], 20, "PDF"], Plot[PDF[WeibullDistribution[α, β], x], {x, 0, 1.5}, PlotStyle -> Thick]]]WaringYuleDistribution 是 GeometricDistribution 与 UniformDistribution 的参数混合：
𝒟 = ParameterMixtureDistribution[GeometricDistribution[w^1 / a], wUniformDistribution[], Assumptions -> a > 0];PDF[𝒟, x]PDF[WaringYuleDistribution[a], x]FullSimplify[% - %%]两个单变量均匀分布的 copula 分布是一个二维均匀分布：
PDF[CopulaDistribution["Product", {UniformDistribution[{a, b}], UniformDistribution[{c, d}]} ], {x, y}]PDF[UniformDistribution[{{a, b}, {c, d}}], {x, y}]% - %%//FullSimplify[#, a < x < b && c < y < d]&可能存在的问题 (2)
当 min 和 max 均不是实数时，UniformDistribution 没有定义：
Mean[UniformDistribution[{3 + I, 4}]]
当 min ≥ max 时，UniformDistribution 没有定义：
Mean[UniformDistribution[{8, 6}]]
Mean[UniformDistribution[{min, max}]] /. {min -> 3 + I}巧妙范例 (1)
绘制不同 max 值的概率密度函数，同时显示 CDF 等高线：
cdf = Function[{x, max}, Evaluate[CDF[UniformDistribution[{0, max}], x]]];
ql = {0.025, 0.10, 0.25, 0.5, 0.75, 0.90, 0.975};
cl = Table[ColorData["Rainbow"][q], {q, Join[{0.0}, ql]}];Legended[Plot3D[PDF[UniformDistribution[{0, max}], x], {x, -2, 6}, {max, 1, 5}, PlotTheme -> "Marketing", MeshFunctions -> {cdf}, Mesh -> {ql}, MeshStyle -> GrayLevel[0.8], MeshShading -> cl, AxesLabel -> Automatic, PlotPoints -> 100, BaseStyle -> Opacity[0.9], ImageSize -> 400, PlotRange -> All, Exclusions -> None], BarLegend["Rainbow", ql, LegendLabel -> "prob"]]
Wolfram Research (2007)，UniformDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/UniformDistribution.html （更新于 2016 年）.
文本
Wolfram Research (2007)，UniformDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/UniformDistribution.html （更新于 2016 年）.
CMS
Wolfram 语言. 2007. "UniformDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/UniformDistribution.html.
APA
Wolfram 语言. (2007). UniformDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/UniformDistribution.html 年