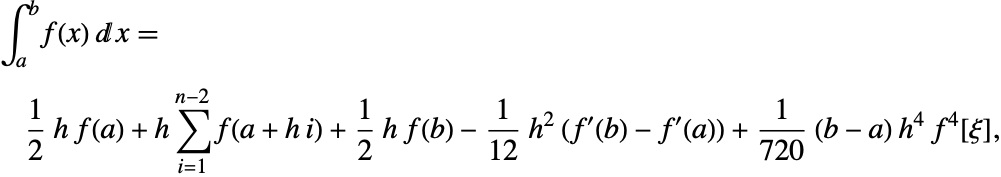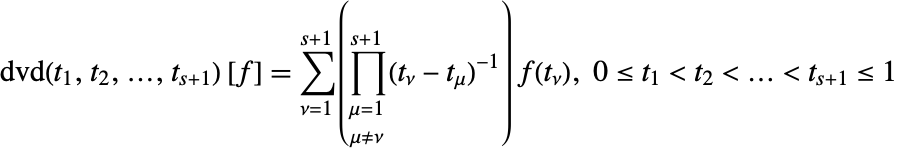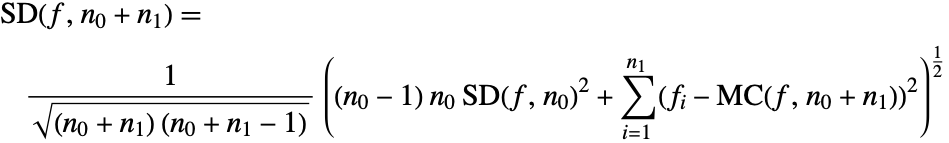-
関数
- AiryAi
- AiryAiPrime
- AiryBi
- AiryBiPrime
- ArcCos
- ArcCosh
- ArcCot
- ArcCoth
- ArcCsc
- ArcCsch
- ArcSec
- ArcSech
- ArcSin
- ArcSinh
- ArcTan
- ArcTanh
- BesselI
- BesselJ
- BesselK
- BesselY
- Beta
- BetaRegularized
- Cos
- Cosh
- CoshIntegral
- CosIntegral
- DawsonF
- DifferentialRoot
- EllipticE
- EllipticK
- Erf
- Erfc
- Erfi
- Exp
- ExpIntegralE
- ExpIntegralEi
- FresnelC
- FresnelS
- Gamma
- GammaRegularized
- HankelH1
- HankelH2
- Haversine
- Hypergeometric0F1
- Hypergeometric0F1Regularized
- Hypergeometric2F1
- Hypergeometric2F1Regularized
- HypergeometricPFQ
- HypergeometricPFQRegularized
- InverseHaversine
- Log
- Power
- Sin
- Sinc
- Sinh
- SinhIntegral
- SinIntegral
- SphericalBesselJ
- StruveH
- StruveL
- 関連するガイド
- テクニカルノート
-
-
関数
- AiryAi
- AiryAiPrime
- AiryBi
- AiryBiPrime
- ArcCos
- ArcCosh
- ArcCot
- ArcCoth
- ArcCsc
- ArcCsch
- ArcSec
- ArcSech
- ArcSin
- ArcSinh
- ArcTan
- ArcTanh
- BesselI
- BesselJ
- BesselK
- BesselY
- Beta
- BetaRegularized
- Cos
- Cosh
- CoshIntegral
- CosIntegral
- DawsonF
- DifferentialRoot
- EllipticE
- EllipticK
- Erf
- Erfc
- Erfi
- Exp
- ExpIntegralE
- ExpIntegralEi
- FresnelC
- FresnelS
- Gamma
- GammaRegularized
- HankelH1
- HankelH2
- Haversine
- Hypergeometric0F1
- Hypergeometric0F1Regularized
- Hypergeometric2F1
- Hypergeometric2F1Regularized
- HypergeometricPFQ
- HypergeometricPFQRegularized
- InverseHaversine
- Log
- Power
- Sin
- Sinc
- Sinh
- SinhIntegral
- SinIntegral
- SphericalBesselJ
- StruveH
- StruveL
- 関連するガイド
- テクニカルノート
-
関数
NIntegrate積分則
はじめに
積分則は,通常重み付き総和を使って領域上の積分推定値を計算する.NIntegrateが使用されるコンテキストでは,積分則オブジェクトは積分推定値,および積分推定値の確度の測定としての誤差推定の両方を与える.
次の一般的な説明は"GaussKronrodRule"や"MultidimensionalRule"等の重み付き総和型の積分則に当てはまる."LevinRule"等,他の型の規則には別の解説が必要である.
積分則はサンプル点と呼ばれる点の集合における被積分関数をサンプリングする.文献ではこれらは分点とも呼ばれる.それぞれのサンプル点 ![]() に対応して重みの数
に対応して重みの数 ![]() がある.積分則は重み付き総和
がある.積分則は重み付き総和![]() で積分
で積分 ![]() を推定する.積分則は関数的であり,区間
を推定する.積分則は関数的であり,区間![]() (あるいはより一般的な領域)上の関数を実数にマップする.
(あるいはより一般的な領域)上の関数を実数にマップする.
規則が領域 ![]() に適用されると,これは
に適用されると,これは ![]() (
(![]() は被積分関数)と表される.
は被積分関数)と表される.
以下で考える規則のサンプル点は区間![]() ,単位立方
,単位立方![]() ,中心化された単位立方
,中心化された単位立方![]() (
(![]() は積分の次元)のいずれかにおける積分の推定値を計算するために選ばれている.よって,
は積分の次元)のいずれかにおける積分の推定値を計算するために選ばれている.よって,![]() がこれらの領域のいずれかであれば,
がこれらの領域のいずれかであれば,![]() の代りに
の代りに ![]() が使われる.これらの規則が他の領域に適用されると,その横座標と推定値はそれに応じてスケールされる.
が使われる.これらの規則が他の領域に適用されると,その横座標と推定値はそれに応じてスケールされる.
積分則 ![]() を関数
を関数 ![]() に適用することは,
に適用することは,![]() の積分といわれる.つまり,
の積分といわれる.つまり,![]() が
が ![]() で積分されると,
で積分されると,![]() を得るのである.
を得るのである.
一次元の積分則で,次数 ![]() 以下の多項式はすべて厳密に積分するが次数
以下の多項式はすべて厳密に積分するが次数 ![]() の多項式のうちの少なくとも1つが失敗する場合,その規則は次数
の多項式のうちの少なくとも1つが失敗する場合,その規則は次数 ![]() と言われる.
と言われる.
多次元の積分則で,次数 ![]() 以下の単項式はすべて厳密に積分するが,次数
以下の単項式はすべて厳密に積分するが,次数 ![]() の単項式の少なくとも1つが失敗する場合,つまり規則が形式
の単項式の少なくとも1つが失敗する場合,つまり規則が形式![]() (
(![]() は次元,
は次元,![]() ,
,![]() )の単項式すべてについてすべて厳密である場合,その規則は次数
)の単項式すべてについてすべて厳密である場合,その規則は次数 ![]() と言われる.
と言われる.
次数 ![]() のヌル規則は,次数
のヌル規則は,次数![]() の単項式すべてについてゼロに積分され,次数
の単項式すべてについてゼロに積分され,次数 ![]() の単項式の少なくともひとつについては失敗する.それぞれのヌル規則は,基本的な積分則と低次元の適切な積分則との差分と考えることができる.
の単項式の少なくともひとつについては失敗する.それぞれのヌル規則は,基本的な積分則と低次元の適切な積分則との差分と考えることができる.
次数 ![]() の規則
の規則 ![]() のサンプル点の集合に低次元の
のサンプル点の集合に低次元の ![]() (
(![]() )の規則
)の規則 ![]() のサンプル点の集合が含まれる場合,
のサンプル点の集合が含まれる場合,![]() は
は ![]() に埋め込まれているという.これは
に埋め込まれているという.これは ![]() と表される.
と表される.
一般的な微分およびプロパティを持つが次数が異なる規則族のメンバーである次数 ![]() の積分則は,
の積分則は,![]() と記述される.ここで
と記述される.ここで ![]() は族を識別するように選ばれる(例えば,次数4の台形規則は
は族を識別するように選ばれる(例えば,次数4の台形規則は ![]() と参照される).
と参照される).
1つの族のそれぞれの規則が同じ族の別の規則に埋め込まれている場合,その族の規則は進行的であるという(ある ![]() に対して
に対して ![]() が存在しそれについて
が存在しそれについて ![]() が成り立つ).
が成り立つ).
積分則は,被積分関数が区間の終点で評価されないならば「開いたタイプ」と呼ばれる.
NIntegrateの積分則オブジェクトは,積分推定に対して1つの積分則と誤差推定に対して1つあるいは複数のヌル規則を持つ.積分則とヌル規則のサンプル点は一致する.「積分則」もしくは「規則」がNIntegrateの積分則オブジェクトを意味するのか,通常の数学的な意味での積分則を意味するのかは,コンテキストから分かるはずである.
積分則の指定
以下で説明する"MonteCarloRule"以外の積分則はすべて,NIntegrateの適応型ストラテジーで使用される.NIntegrateでは,モンテカルロ法は単純でも適応型でも"MonteCarloRule"を使う.
積分ストラテジーの積分則要素を変更すると,異なる積分法になる.
NIntegrateの適応型ストラテジー(「大域的適応ストラテジー」と「局所的適応ストラテジー」を参照)で使用する積分則を指定するためには,Methodサブオプションを使う.
NIntegrateに積分則指定("MonteCarloRule"以外)だけを持つメソッドオプションが与えられると,その規則は"GlobalAdaptive"ストラテジーで使われる.以下の2つの入力は同等である.
"MonteCarloRule"では,適応型モンテカルロストラテジーが自動的に使用される.下の2つのコマンドは等価である.
"TrapezoidalRule"
積分推定における台形規則は最も簡単で昔からある規則の一つである(古代ギリシャの数学者により使われ,バビロン人にも使われた可能性がある).
Methodオプションに値"TrapezoidalRule"が与えられると,複合台形規則は積分則により形成された各部分区間を推定するために使われる.
オプション名
|
デフォルト値
| |
| "Points" | 5 | 粗い台形の点の数 |
| "RombergQuadrature" | True | ロンバーグ(Romberg)積分法を使うかどうか |
| "SymbolicProcessing" | Automatic | 記号的前処理を実行する秒数 |
台形規則およびその複合(マルチパネル)拡張はあまり正確ではない.複合台形規則は線形関数については厳密であり,被積分関数が連続の第二導関数を持つなら少なくとも ![]() の速さで収束する[DavRab84].マルチパネル台形規則の正確さはロンバーグ求積法を使うと増加させることができる.
の速さで収束する[DavRab84].マルチパネル台形規則の正確さはロンバーグ求積法を使うと増加させることができる.
![]() の横軸は
の横軸は ![]() の部分集合であるため,差分
の部分集合であるため,差分![]() は積分推定値
は積分推定値 ![]() の誤差推定を取ることができ,追加の被積分関数の評価をしないで計算することができる.
の誤差推定を取ることができ,追加の被積分関数の評価をしないで計算することができる.
オプション"Points"->k はいくつの粗い点を使うかを指定するために使うことができる."TrapezoidalRule"で使用される点の合計数は![]() である.
である.
注意:NIntegrateには台形規則と台形ストラテジーの両方がある.「積分ストラテジー」チュートリアルの「台形ストラテジー」を参照のこと.NIntegrateの内部的に実装された積分則はすべて-Ruleという接尾辞を持つ.よって,"TrapezoidalRule"は台形積分則を指定するために使われ,"Trapezoidal"は積分ストラテジーを指定するために使われる.
ロンバーグ積分法
ロンバーグ積分法とは,![]() と
と ![]() の打ち切り近似誤差の同じ次数項を除去する
の打ち切り近似誤差の同じ次数項を除去する ![]() と
と ![]() の線形結合を使うものである.
の線形結合を使うものである.
オイラー・マクローリン(Euler–Maclaurin)公式[DavRab84]から
上の方程式の ![]() 項は,2つ目の方程式から最初の方程式を4回引くと除去することができる.結果は下のようになる.
項は,2つ目の方程式から最初の方程式を4回引くと除去することができる.結果は下のようになる.
"TrapezoidalRule"のサンプル点と重み
"NewtonCotesRule"
ニュートン・コーツ(Newton–Cotes)積分公式は,等間隔のサンプル点を持つ補間タイプの公式である.
オプション名
|
デフォルト値
| |
| "Points" | 3 | 粗いニュートン・コーツ点の数 |
| "Type" | Closed | ニュートン・コーツ規則のタイプ |
| "SymbolicProcessing" | Automatic | 記号的前処理を実行する秒数 |
で,等間隔の ![]() 個の部分区間に分けるとする.すると,補間タイプの積分公式は
個の部分区間に分けるとする.すると,補間タイプの積分公式は
である.![]() が大きいとき,ニュートン・コーツの
が大きいとき,ニュートン・コーツの ![]() 点係数は大きく,符号も混在する.
点係数は大きく,符号も混在する.
これでは桁落ちにより多数の有効数字が失われる可能性があるため,高次のニュートン・コーツ規則は注意して使う必要がある.
"NewtonCotesRule"のサンプル点と重み
"GaussBerntsenEspelidRule"
ガウス積分法では,最適サンプル点を使い(多項式補間による),これらの点上での被積分関数値の重み付き総和を形成する.これらのサンプル点の部分集合上で,低次数の積分則が作られる.2つの規則の差分は誤差を推定するために使うことができる.BerntsenとEspelidは,奇数のサンプル点を使ってガウス規則の中点を削除することにより誤差推定規則を導き出した.
"GaussBerntsenEspelidRule"オプション
被積分関数 ![]() に対する
に対する ![]() 点のガウス規則
点のガウス規則 ![]() は,次数
は,次数![]() の多項式の場合厳密である(つまり,
の多項式の場合厳密である(つまり,![]() が次数
が次数![]() の多項式ならば
の多項式ならば ![]() である).
である).
ガウス規則では被積分関数が区間の終点で評価されないので,開いたタイプである(Lobatto規則,クレンショウ・カーチス則,台形規則は区間の終点で積分評価を使うので閉じたタイプである).
差分商関数[Ehrich2000]を定義する.
ガウス規則 ![]() のサンプル点が
のサンプル点が ![]() であったら,BerntsenとEspelidは以下の誤差推定関数を導いていたことになる([Ehrich2000]を参照).
であったら,BerntsenとEspelidは以下の誤差推定関数を導いていたことになる([Ehrich2000]を参照).
([Ehrich2000]のもとの公式は![]() のサンプル点のためのものである.上の公式は
のサンプル点のためのものである.上の公式は![]() のサンプル点のためのものである.)
のサンプル点のためのものである.)
"GaussBerntsenEspelidRule"のサンプル点と重み
Berntsen-Espelidの誤差の重みは以下で実装される.
"GaussKronrodRule"
ガウス積分法は最適サンプル点(多項式補間による)を使い,これらの点上の被積分関数値の重み付き総和を形成する.ガウス規則のクロンロッド拡張は,ガウス点の間に新しいサンプル点を加え,ガウス規則の被積分関数評価を再利用する高次の規則を形成する.
被積分関数 ![]() に対する
に対する ![]() 点のガウス規則
点のガウス規則 ![]() は,次数
は,次数![]() の多項式の場合厳密である(つまり,
の多項式の場合厳密である(つまり,![]() が次数
が次数![]() の多項式ならば
の多項式ならば ![]() である).
である).
ガウス・クロンロッド規則では被積分関数は区間の終点で評価されないので,開いたタイプである.
![]() 点のガウス規則
点のガウス規則 ![]() のクロンロッド拡張
のクロンロッド拡張![]() は,
は,![]() に
に ![]() 個の点を加える.拡張された規則は
個の点を加える.拡張された規則は ![]() が偶数の場合次数
が偶数の場合次数![]() の多項式に対して,
の多項式に対して,![]() が奇数の場合は
が奇数の場合は![]() の多項式に対して厳密である.ガウス規則に関連付けられた重みはそのクロンロッド拡張で変化する.
の多項式に対して厳密である.ガウス規則に関連付けられた重みはそのクロンロッド拡張で変化する.
![]() の横座標は
の横座標は![]() の部分集合なので,差分
の部分集合なので,差分![]() は積分誤差
は積分誤差![]() の誤差推定とされ,余分な被積分関数の評価なしで計算することができる.
の誤差推定とされ,余分な被積分関数の評価なしで計算することができる.
ガウス規則のクロンロッド拡張の実装の記述は[PiesBrand74]を参照のこと.
"GaussKronrodRule"のサンプル点と重み
下の計算は,ガウス・クロンロッド積分則(上を参照)の次数を示している.
下のコマンドは積分推定値に対する積分則の重み付き総和 ![]() および誤差推定
および誤差推定 ![]() を実装する.ここで
を実装する.ここで![]() は横座標,
は横座標,![]() は重み,
は重み,![]() は誤差の重みである.
は誤差の重みである.
上の誤差推定は,埋め込まれたガウス規則が次数![]() の多項式に対して厳密であるため,ゼロにはならない.もしその次数の多項式を積分したら,誤差推定はゼロになる.
の多項式に対して厳密であるため,ゼロにはならない.もしその次数の多項式を積分したら,誤差推定はゼロになる.
"LobattoKronrodRule"
Lobatto積分則は事前に割り当てられた横座標を持つガウスタイプの規則である.これは積分区間の終点と区間内の最適サンプル点を使い,これらの点上の被積分関数値の重み付き総和を形成する.Lobatto規則のクロンロッド拡張は,Lobatto規則点の間に新しいサンプル点を加え,Lobatto規則の被積分関数の評価を再利用する高次の規則を形成する.
オプション名
|
デフォルト値
| |
| "Points" | 5 | クロンロッド点で拡張されるガウス・Lobatto点の数 |
| "SymbolicProcessing" | Automatic | 記号的前処理を実行する秒数 |
被積分関数 ![]() の
の ![]() 点のLobatto規則
点のLobatto規則 ![]() は,次数
は,次数![]() の多項式について厳密である(
の多項式について厳密である(![]() が次数
が次数![]() の多項式ならば
の多項式ならば ![]() である).
である).
![]() 点のLobatto規則
点のLobatto規則 ![]() のクロンロッド拡張
のクロンロッド拡張![]() は
は ![]() に
に ![]() 個の点を加える.拡張された規則は
個の点を加える.拡張された規則は ![]() が偶数ならば次数
が偶数ならば次数![]() の多項式に対して,
の多項式に対して,![]() が奇数ならば
が奇数ならば![]() の多項式に対して厳密である.Lobatto規則に関連付けられた重みはそのクロンロッド拡張で変化する.
の多項式に対して厳密である.Lobatto規則に関連付けられた重みはそのクロンロッド拡張で変化する.
"GaussKronrodRule"と同様に,ガウス点の数はオプション"GaussPoints"で指定される.もし"LobattoKronrodRule"が"Points"->n で使われると,規則の点の合計数は![]() になる.
になる.
Lobatto規則は閉じた規則なので,被積分関数は区間の終点で評価されなければならない.これらの点に特異性がある場合,NIntegrateはそれを無視する.
Lobatto規則のクロンロッド拡張の実装の詳細は[PiesBrand74]を参照のこと.
"LobattoKronrodRule"のサンプル点と重み
下の計算はLobatto・クロンロッド積分則の次数を示す(上を参照).
下のコマンドは積分推定に対する積分則の重み付き総和 ![]() と誤差推定
と誤差推定 ![]() を実装する.ここで
を実装する.ここで ![]() は横座標,
は横座標,![]() は重み,
は重み,![]() は誤差の重みである.
は誤差の重みである.
埋め込まれたLobatto規則は次数![]() の多項式に対して厳密なので,上の誤差推定はゼロにはならない.もしその次数の多項式を積分したならば,誤差推定はゼロになる.
の多項式に対して厳密なので,上の誤差推定はゼロにはならない.もしその次数の多項式を積分したならば,誤差推定はゼロになる.
"ClenshawCurtisRule"
クレンショウ・カーチス(Clenshaw–Curtis)則は被積分関数のチェビシェフ(Chebyshev)多項式近似から導かれたサンプル点を使用する.
オプション名
|
デフォルト値
| |
| "Points" | 5 | 粗いクレンショウ・カーチスの点 |
| "SymbolicProcessing" | Automatic | 記号的処理を実行する秒数 |
![]() 個のサンプル点を持つクレンショウ・カーチス則は理論的に次数
個のサンプル点を持つクレンショウ・カーチス則は理論的に次数 ![]() 以下の多項式に対して厳密である.しかし,実際にはクレンショウ・カーチス則はガウス則の確度を達成する[Evans93][OHaraSmith68].クレンショウ・カーチス公式の誤差は[OHaraSmith68]で解析されている.
以下の多項式に対して厳密である.しかし,実際にはクレンショウ・カーチス則はガウス則の確度を達成する[Evans93][OHaraSmith68].クレンショウ・カーチス公式の誤差は[OHaraSmith68]で解析されている.
伝統的なクレンショウ・カーチス則のサンプル点は,チェビシェフ多項式の零点である.実践的なクレンショウ・カーチス則のサンプル点はチェビシェフ多項式の極値となるよう選ばれる.伝統的なクレンショウ・カーチス則は進行的でないが実践的なクレンショウ・カーチス則は進行的である[DavRab84][KrUeb98].
![]() が,関数
が,関数 ![]() の
の ![]() 個のサンプル点の実践的なクレンショウ・カーチス則を表すとする.
個のサンプル点の実践的なクレンショウ・カーチス則を表すとする.
進行的属性は,![]() のサンプル点が
のサンプル点が![]() のサンプル点の部分集合であることを意味する.よって,差分
のサンプル点の部分集合であることを意味する.よって,差分![]() は積分推定
は積分推定![]() の誤差推定とすることができ,余分な被積分関数評価なしで計算することができる.
の誤差推定とすることができ,余分な被積分関数評価なしで計算することができる.
"ClenshawCurtisRule"のサンプル点と重み
"MultipanelRule"
"MultipanelRule"は2つ以上の隣接区間上の一次元積分則の適用を1つの規則に結合する.隣接区間のいずれかにもとの規則を適用することをパネルと呼ぶ.
オプション名
|
デフォルト値
| |
| Method | "NewtonCotesRule" | 1つのパネルに対する横座標,重み,誤差の重みを提供する積分則指定 |
| "Panels" | 5 | パネルの数 |
| "SymbolicProcessing" | Automatic | 記号的処理を実行する秒数 |
に変換される.ここで ![]() ,
,![]() ,
,![]() とすると,
とすると,![]() に基づく
に基づく ![]() パネルの積分規則は明示的に
パネルの積分規則は明示的に
と書くことができる.もし ![]() が閉じている(
が閉じている(![]() がサンプル点として
がサンプル点として![]() と
と![]() を持つ)ならば,
を持つ)ならば,![]() であり,
であり,![]() のサンプル点の数は
のサンプル点の数は ![]() に還元される(これは"MultipanelRule"の実装で実行される).
に還元される(これは"MultipanelRule"の実装で実行される).
マルチパネル則(複合則とも呼ばれる)の理論は[KrUeb98]および[DavRab84]に記述されている.
"MultipanelRule"のサンプル点と重み
"CartesianRule"
![]() 次元の直積型積分則は
次元の直積型積分則は ![]() 個の一次元則のサンプル点の直積であるサンプル積を持つ.直積型積分則のサンプル点に関連付けられた重みは,座標に対応する一次元則の重みの積である.
個の一次元則のサンプル点の直積であるサンプル積を持つ.直積型積分則のサンプル点に関連付けられた重みは,座標に対応する一次元則の重みの積である.
オプション名
|
デフォルト値
| |
| Method | "GaussKronrodRule" | 直積型積分則が形成される規則あるいは規則のリスト |
| "SymbolicProcessing" | Automatic | 記号的処理を実行する秒数 |
これらはそれぞれ次数 ![]() ,
,![]() ,
,![]() の多項式に対して厳密である.よって
の多項式に対して厳密である.よって ![]() 個の点を持つ公式
個の点を持つ公式
が次数![]() の
の ![]() の多項式に対して厳密であることは簡単に分かる.分点
の多項式に対して厳密であることは簡単に分かる.分点![]() に関連付けられた重みは
に関連付けられた重みは ![]() である.
である.
![]() が
が ![]() 個のサンプル点
個のサンプル点![]() と重み
と重み![]() を持つような,
を持つような,![]() 個の一次元則に対する一般的な直積の公式は,以下の通りである.
個の一次元則に対する一般的な直積の公式は,以下の通りである.
と書くことができる.ここで ![]() であり,各整数
であり,各整数 ![]() について
について ![]() であり
であり ![]() である.
である.
直積型積分則は比較的低い次元(![]() )に適用できる.それは高次元では,「組合せ的爆発」の対象となるからである.例えば,それぞれが
)に適用できる.それは高次元では,「組合せ的爆発」の対象となるからである.例えば,それぞれが![]() 個のサンプル点を持つ
個のサンプル点を持つ![]() つの同一の一次元則の
つの同一の一次元則の![]() 次元直積は
次元直積は![]() 個のサンプル点を持つ.
個のサンプル点を持つ.
NIntegrateでは,積分が多次元であり,Methodオプションに一次元則あるいは一次元則のリストが与えられている場合に直積型積分則が使われる.
直積型積分則についての詳細は[Stroud71]に記載されている.
"CartesianRule"のサンプル点と重み
NIntegrate`CartesianRuleDataはそれぞれの規則の横座標と重みとを別々にしておく.そうでないと(3)から分かるように,高次元の場合に結果が大きすぎることがあるからである.
"MultidimensionalRule"
立方体![]() (ここで
(ここで ![]() )に対する完全対称則は次の2つの属性を持つ点の集合からなる.まず1つ目は,集合内のすべての点は,その集合の任意の固定点の座標の置換および/または符号変更により生成できるというものである.2つ目は,その集合のすべての点は関連付けられた同じ重さの重みを持つということである.
)に対する完全対称則は次の2つの属性を持つ点の集合からなる.まず1つ目は,集合内のすべての点は,その集合の任意の固定点の座標の置換および/または符号変更により生成できるというものである.2つ目は,その集合のすべての点は関連付けられた同じ重さの重みを持つということである.
上の属性を満足する完全対称則の点集合は軌道と呼ばれる.不等式 ![]() が成り立つ座標に対する軌道上の点
が成り立つ座標に対する軌道上の点![]() はジェネレータと呼ばれる([KrUeb98][GenzMalik83]を参照のこと).
はジェネレータと呼ばれる([KrUeb98][GenzMalik83]を参照のこと).
オプション名
|
デフォルト値
| |
| "Generators" | 5 | 完全対称則のジェネレータの数 |
| "SymbolicProcessing" | Automatic | 記号的前処理を実行する秒数 |
積分則が![]() で表される
で表される ![]() 個の軌道を持つ場合,その
個の軌道を持つ場合,その ![]() 番目
番目 ![]() はそれに関連付けられた重み
はそれに関連付けられた重み ![]() を持ち,積分推定値は以下の式
を持ち,積分推定値は以下の式
で計算される.次数 ![]() のヌル規則は,次数
のヌル規則は,次数![]() のすべての単項式でゼロに積分され,次数
のすべての単項式でゼロに積分され,次数 ![]() の少なくとも1つの単項式ではそれに失敗する.それぞれのヌル規則は基礎的な積分則と低次数の適切な積分との間の差分と考えることができる.
の少なくとも1つの単項式ではそれに失敗する.それぞれのヌル規則は基礎的な積分則と低次数の適切な積分との間の差分と考えることができる.
NIntegrateの"MultidimensionalRule"オブジェクトは基本的に,1つの積分則と1つあるいはそれ以上のヌル規則とを合せた3つの異なる積分則オブジェクトのインターフェースである.そのジェネレータ数と次数は下の表にまとめてある.6個または9個のジェネレータを持つ規則オブジェクトは3つのヌル規則を使い,それぞれが2つのヌル規則の線形結合である.ヌル規則の線形結合は位相誤差を避けるために使われる.ヌル規則がどのように使われるかは[BerntEspGenz91]を参照のこと.
| ジェネレータ数 | 積分則次数 | それぞれのヌル規則の次数 | 参照 |
| 5 | 7 | 5 | [GenzMalik80] |
| 6 | 7 | 5,3,1 | [GenzMalik83][BerntEspGenz91] |
| 9 | 9 | 7,5,3 | [GenzMalik83][BerntEspGenz91] |
"MultidimensionalRule"のサンプル点と重み
"LevinRule"
レビン型規則は,不定積分を被積分関数の多項式と振動部の積として近似することにより振動関数の積分を推定する.
"LevinRule"はデフォルトで,自動的に被積分関数の振動部を検知し,下で説明する選点法を適用して積分推定を形成する.振動部を指定するためのオプション,および非振動の別の積分則へと適宜切り替えるかどうか等を含む数値法の細かい動作を制御するオプションを使うことができる.
オプション名
|
デフォルト値
| |
| "Points" | Automatic | 粗い選点の数 |
| "EndpointLimitTerms" | Automatic | 非数値の終点における多項式補間の次数 |
| "TimeConstraint" | 10 | 積分ステップ毎に選点方程式を解く最大限の時間 |
| "MethodSwitching" | True | 非振動の規則へ自動的に切り替えるかどうか |
| "OscillationThreshold" | 10 | "LevinRule"を適用し始める,最小の振動の概数 |
| Method | Automatic | 別の非振動規則 |
| "LevinFunctions" | Automatic | カーネルに含ませる振動関数 |
| "MaxOrder" | 50 | カーネルの最大微分階数 |
| ExcludedForms | {} | カーネルから除外する形式 |
| "AdditiveTerm" | Automatic | 被積分関数の加算的な非振動部 |
| "Amplitude" | Automatic | 被積分関数でのカーネルの係数 |
| "DifferentialMatrix" | Automatic | カーネルにより満足される線形常微分方程式の行列形式 |
| "Kernel" | Automatic | 明示的な振動カーネル |
レビン型選点法
スコープ
一次元の数値積分に対する基本的なレビン型のメソッド[Levin96]は次の形式の振動関数に適用される.
ここで振動部 ![]() は次の行列形式で書かれる階数
は次の行列形式で書かれる階数 ![]() の線形常微分方程式を満足しなければならない.
の線形常微分方程式を満足しなければならない.
この ![]() は
は ![]() の一つである.関数
の一つである.関数 ![]() のベクトルは振動カーネルであり,行列
のベクトルは振動カーネルであり,行列 ![]() は微分行列である.
は微分行列である.
を扱うこともできる.上のより単純な場合は,通常 ![]() および
および ![]() である.関数
である.関数 ![]() のベクトルは振幅である.
のベクトルは振幅である.
Exp,BesselJ,AiryAi等,数学における振動する特殊関数のほとんどは,線形常微分方程式を満足するため,レビン型メソッドを使って積分することができる.さらに,このような関数の積,総和,整数ベキ,高速でない振動関数との合成関数もすべて線形常微分方程式を満足する.DifferentialRootReduceも参照のこと.
"LevinRule"法は次のような,わずかにより一般的なクラスにも適用することができる.
ここで加算項 ![]() は"GaussKronrodRule"等の従来の求積法で別に扱われる.
は"GaussKronrodRule"等の従来の求積法で別に扱われる.
レビン型メソッドは,振幅 ![]() ,加算項
,加算項 ![]() ,微分行列
,微分行列 ![]() 自身が高速で振動しないときに効果的である[Levin97].
自身が高速で振動しないときに効果的である[Levin97].
選点法
レビン型の選点法では,ある未知の関数![]() に対して被積分関数
に対して被積分関数![]() の不定積分が形式
の不定積分が形式![]() で求められる.
で求められる.
![]() について両辺を微分し,
について両辺を微分し,![]() を使うと,すべての
を使うと,すべての ![]() が打ち消され,関数
が打ち消され,関数 ![]() が非振動の微分方程式を満足することが分かる.
が非振動の微分方程式を満足することが分かる.
これらの方程式は,選点法を使って ![]() について解くことができる.選点法では,それぞれの
について解くことができる.選点法では,それぞれの ![]() を
を ![]() 個の既定された基底関数
個の既定された基底関数 ![]() の単純集合の線形結合として近似する.
の単純集合の線形結合として近似する.
"LevinRule"では,基底関数 ![]() はチェビシェフ(Chebyshev)の多項式ChebyshevT[k,x]となるよう選ばれる.これを
はチェビシェフ(Chebyshev)の多項式ChebyshevT[k,x]となるよう選ばれる.これを ![]() の微分方程式に代入すると,
の微分方程式に代入すると,![]() 個の選点の係数
個の選点の係数 ![]() に対する
に対する ![]() 個の線形方程式ができる.
個の線形方程式ができる.
![]() ,
,![]() ,
,![]() ,
,![]() はすべて既知の関数なので,積分領域内の
はすべて既知の関数なので,積分領域内の ![]() 個の選点ノード
個の選点ノード![]() でこれらの線形関数を評価することができる.これにより,
でこれらの線形関数を評価することができる.これにより,![]() 個の係数
個の係数 ![]() に対する
に対する ![]() 個の線形方程式ができる.これらの方程式を数値的に解くと,
個の線形方程式ができる.これらの方程式を数値的に解くと,![]() に対する近似形式が得られ,次のように微積分学の基本定理を使って直接積分を評価できるようになる.
に対する近似形式が得られ,次のように微積分学の基本定理を使って直接積分を評価できるようになる.
NIntegrateでは,選点ノード![]() として対応する"GaussKronrodRule"の分点が使われる.
として対応する"GaussKronrodRule"の分点が使われる.
"LevinRule"は ![]() 個の選点ノードを使って積分推定を計算する.ここで
個の選点ノードを使って積分推定を計算する.ここで ![]() は"Points"メソッドオプションの値である.階数の低い積分推定値もまた,2つおきの選点ノード(
は"Points"メソッドオプションの値である.階数の低い積分推定値もまた,2つおきの選点ノード(![]() )を使って計算される.これら2つの積分推定値の差分はアルゴリズムの誤差推定として取られる.
)を使って計算される.これら2つの積分推定値の差分はアルゴリズムの誤差推定として取られる.
振動カーネルの指定
デフォルトでは"LevinRule"は,できるだけ被積分関数を包含する振動カーネルを自動的に選ぶ.この動作はオプションを使って細部に渡り変更することができる.
被積分関数に,積分領域上であまり高振動ではない振動関数が含まれている場合,振動カーネルからそれを除外した方が効率よくなる可能性がある.例えば,Sin[x]は領域{x,0,5}上ではあまり高振動ではない.
被積分関数の振動部を指定するためには,"Kernel"メソッドオプションを使うことができる.
"ExcludedForms"メソッドは,自動的に検出される振動カーネルに含まれるべきではない被積分関数の部分を指定するために使うことができる.
"LevinFunctions"メソッドオプションは,自動的に検出される振動カーネルに含まれる関数のタイプを指定するために使うことができる.設定"LevinFunctions"->{h1,h2,…}は特定の関数 hi のみを検出する.
設定"LevinFunctions"->{grp1,grp2,…}は名前付きのグループ grpi から関数を検出する.
| "ExpRelated" | Exp,Power |
| "TrigRelated" | Sin,Cos,Sinh,Cosh,Haversine,Sinc |
| "ErfRelated" | Erf,Erfc,Erfi |
| "TrigIntegrals" | FresnelS,FresnelC,SinIntegral,CosIntegral,SinhIntegral,CoshIntegral |
| "BesselRelated" | BesselJ,BesselY,HankelH1,BesselI,BesselK,HankelH2,StruveH,StruveL,SphericalBesselJ |
| "AiryRelated" | AiryAi,AiryAiPrime,AiryBi,AiryBiPrime |
| "HypergeometricRelated" | HypergeometricPFQ,HypergeometricPFQRegularized,Hypergeometric0F1,Hypergeometric0F1Regularized,Hypergeometric2F1,Hypergeometric2F1Regularized |
| "InverseTrig" | ArcSin,ArcCos,ArcSinh,ArcCosh,ArcSec,ArcCsc,ArcSech,ArcCsch,ArcTan,ArcCot,ArcTanh,ArcCoth,InverseHaversine |
| "Elliptic" | EllipticE,EllipticK |
| "GammaRelated" | Gamma,GammaRegularized,Beta,BetaRegularized |
| "ExpIntegrals" | ExpIntegralE,ExpIntegralEi,DawsonF |
| "DifferentialRoots" | DifferentialRootオブジェクト |
| "Other" | Log |
"LevinFunctions"メソッドオプションで認識される名前付きグループ
デフォルトでは"LevinFunctions"の設定には"Other","InverseTrig","Elliptic"以外の名前付きグループがすべて含まれる.この設定は,領域内のいずれかの部分で振動する初等関数および特殊関数に対応する.
NIntegrate`LevinIntegrandオブジェクト
NIntegrateにより検出された振動カーネル,差分行列,振幅,加算項を,内部関数NIntegrate`LevinIntegrandReduceを使って詳細に調べることができる.NIntegrate`LevinIntegrandReduceは,レビン型の選点法を適用することのできる完全に処理された被積分関数を表すNIntegrate`LevinIntegrandオブジェクトを返す.
NIntegrate`LevinIntegrandオブジェクト li のプロパティは,形式 li["prop"] を使ってアクセスすることができる.
"Rules"プロパティは,レビン型の選点法で使われるNIntegrate`LevinIntegrandの主なプロパティを与える.
このプロパティを使うことで,振動カーネル検出に対する"AdditiveTerm"オプション等の異なる"LevinRule"メソッドオプションの効果をすくに見ることができる.
被積分関数に関数のグループを含める,あるいはそれから除外するために"LevinFunctions"オプションを使う方法が分かる.
被積分関数の分解における4つの部分(加算項,振幅,カーネル,差分行列)すべてを完全に指定することができる.これは同様の被積分関数でNIntegrateを複数回効率よく呼び出すときに便利である.
この場合,NIntegrateの第1引数が完全に無視されることに注意する.
"MonteCarloRule"
モンテカルロ則はランダム(擬似ランダム)なサンプル点上で一様に重みの付いた被積分関数評価の総和を形成することにより,積分を推定する.
オプション名
|
デフォルト値
| |
| "Points" | 100 | サンプル点の数 |
| "PointGenerator" | Random | サンプル点座標ジェネレータ |
| "AxisSelector" | Automatic | 大域的適応的モンテカルロ積分が使用されたときに軸を分割する選択アルゴリズム |
| "SymbolicProcessing" | Automatic | 記号的前処理を実行する秒数 |
モンテカルロ法[KrUeb98]では,![]() 次元積分
次元積分 ![]() は次の期待(平均)値と解釈される.
は次の期待(平均)値と解釈される.
ここで ![]() は,
は,![]() 上の一様分布,つまり確率密度が
上の一様分布,つまり確率密度が![]() の分布について,乱数変数として解釈される関数
の分布について,乱数変数として解釈される関数 ![]() の平均値である.領域
の平均値である.領域 ![]() の特性関数は
の特性関数は![]() と表され,
と表され,![]() の体積は
の体積は![]() と表される.
と表される.
期待値 ![]() の単純モンテカルロ推定値は,
の単純モンテカルロ推定値は,![]() 個の独立した乱数ベクトル
個の独立した乱数ベクトル![]() を密度
を密度![]() で取る(つまりベクトルは
で取る(つまりベクトルは ![]() 上で一様に分布するということ)ことで得られ,以下の推定値が求められる.
上で一様に分布するということ)ことで得られ,以下の推定値が求められる.
注意.関数![]() は
は![]() および
および ![]() 全体で非負であるため,有効な確率密度関数である.
全体で非負であるため,有効な確率密度関数である.
は確率![]() で起る.大数の法則は誤差
で起る.大数の法則は誤差![]() に関する情報は提供しないので,確率的推定が使われる.
に関する情報は提供しないので,確率的推定が使われる.
と定義されるとする.式(5)は ![]() の不偏推定値(
の不偏推定値(![]() のさまざまな集合に対する
のさまざまな集合に対する![]() の期待値が
の期待値が ![]() ということ)であり,その分散は
ということ)であり,その分散は
方程式(6)から分かるが,単純モンテカルロ推定値の収束率は積分の次元 ![]() に依存しておらず,
に依存しておらず,![]() 個のサンプル点が使われるならば収束率は
個のサンプル点が使われるならば収束率は![]() になる.
になる.
NIntegrateの積分則"MonteCarloRule"は推定値![]() と
と![]() を計算する.
を計算する.
推定値は付加的に向上させることができる.つまり,もし推定値が![]() と
と![]() であり,新しい付加的なサンプル関数値
であり,新しい付加的なサンプル関数値![]() の集合があるならば,(7)と(8)を使い,下が求められる.
の集合があるならば,(7)と(8)を使い,下が求められる.
推定値![]() と
と![]() を求めるためには,推定値
を求めるためには,推定値![]() と
と![]() を計算するために使われた乱数点が分かっている必要はない.
を計算するために使われた乱数点が分かっている必要はない.
"AxisSelector"
"MonteCarloRule"が多次元の大域的適応型積分に対して使われるとき,それは2つの方法で適用される積分部分領域の分割軸を選ぶ.1つ目の選び方は無作為な選び方である.2つ目は,部分領域が軸に沿って分割される場合に,その部分領域のそれぞれの積分推定値の分散の和が最小になるようにする方法である.
無作為な軸の選択は次のように行われる."MonteCarloRule"が選択に使用する軸の集合 ![]() を保持する.初めは
を保持する.初めは ![]() にすべての軸が含まれる.
にすべての軸が含まれる.![]() の要素が無作為に選択される.選択された軸は
の要素が無作為に選択される.選択された軸は ![]() から除かれる.次の積分推定の後,軸が
から除かれる.次の積分推定の後,軸が ![]() から選ばれそこから除外される.これが継続していく.
から選ばれそこから除外される.これが継続していく.![]() が空になると,すべての軸で補充される.
が空になると,すべての軸で補充される.
分散最小化の軸選択は次のように行われる.領域上での積分中,サンプル点の部分集合とその被積分関数値が保存される.次に,すべての軸に対して,軸に沿った分割で生成される2つの部分領域の分散が,保存されているサンプル点と対応する被積分関数値を使って推定される.これらの分散の総和が最小となる軸が分割軸として選ばれる.領域がその軸で分割されると新しい積分誤差推定が最小となるということを意味するからである.ある軸について,すべての保存されている点が半領域のどちらかでクラスタ化されると,その軸が分割に選ばれる.
オプション値
| |
| Random | 無作為な分割軸の選択 |
| MinVariance|{MinVariance, "SubsampleFraction"->frac} | 新しい領域の分散和を最小にするような分割軸の選択 |
下の例では,2つの軸選択アルゴリズムを比較する.一般に分散最小化の選択法の方が使用するサンプル点の数が少ない.しかしこの方法を使うと"MonteCarloRule"が遅くなる.よって,どちらの軸選択方法でも同数のサンプル点を使う結果になるような積分では,無作為選択法を使った方が速い.また,分散最小化の分割軸を選ぶために多数のサンプル点を使うと積分が遅くなる.
規則の比較
"MonteCarloRule"以外の積分則はすべてNIntegrateの適応型ストラテジーで使われる.積分ストラテジーに対して積分則の要素のタイプや点の数を変更することで,異なる積分アルゴリズムとなる.一般に,これらの異なる積分アルゴリズムは,異なる積分に対して実行方法が異なる.そこで次のような問題が生じる.
1. すべての積分,あるいはあるタイプの積分に対して,他よりもよいという規則のタイプがあるか.
2. 積分ストラテジーが与えられると,どの規則がそれとうまく動作するか.また,どの積分に対してか.
3. 積分,積分ストラテジー,積分則が与えられた場合,規則の中の何番の点が,目標精度を満足する積分推定値に到達するために使用されるサンプル点の合計数を最小化するか.
指定された積分,積分ストラテジーで,サンプル点の最少数で目標精度を満足する結果に達する積分則のことを最適積分則という.最適積分則を決定するいくつかの要因を挙げる.
4. 一般に,規則の次数が高いほど,滑らかな被積分関数および高い目標精度での積分は速くなる.一方,被積分関数に対して規則の次数が高すぎると,適応ストラテジーを使うときに使用されるサンプル点が多すぎる.
5. 規則の誤差推定汎関数は,積分ストラテジーによる仕事の総量に大きく影響を及ぼす.少数の点を持つ規則は,(1)積分の過小評価のために誤った結果となるか (2) 積分の過大評価のために多すぎるサンプル点を適用することになるかのどちらかである(「異常な挙動の例」を参照のこと).さらに,誤差推定汎関数は1つあるいはいくつかの埋め込まれたヌル規則で計算されることがある.一般に,ヌル規則の数が多いほど,誤差推定はよくなる.位相誤差が小さくなるからである.ヌル規則の数と誤差推定を計算する総和においてそのヌル規則に割り当てられた重みは,異常な積分およびその規則では計算しにくい積分の集合を決定する(NIntegrateの多次元規則の中には,誤差推定を計算するためにいくつかの組み込まれたヌル規則を使うものもある.NIntegrateの一次元積分則はすべてヌル規則を1つだけ使う).
6. 局所的適応型ストラテジーは,開規則(GaussKronrodRule等)やサンプル点が非一様に分布する閉規則("LobattoKronrodRule"等)よりも,サンプル点がより一様に分布する閉規則("ClenshawCurtisRule"等)でより効率的である.
7. ストラテジーにより再使用される点の割合により何が最適の規則かが決まる.一次元積分では,"LocalAdaptive"は閉規則のすべての点を再使用する."GlobalAdaptive"は誤差推定値の向上が必要である領域のほぼすべての点を捨てる.
規則の中の点の数
ここでは,被積分関数が滑らかで目標精度が高い場合,規則の次数が高いほど積分が速いという例題を挙げる.また,被積分関数に対して規則の次数が高すぎるため,適応ストラテジーが被積分関数の非連続性を操作する場合に使うサンプル点が多すぎるという例も示す.すべての例題にはガウス則のBerntsen–Espelid誤差推定が使われている.
である([DavRab84]を参照).
サンプル点の最少数
規則の比較
異常な挙動の例
誤差推定器をごまかす
ここではNIntegrateが被積分関数の部分を検出することができないため,デフォルト設定で過小評価する積分について説明する.その部分は目標精度を上げると検出される.
誤った推定値
よりよい結果
推定器が誤解される理由
上のプロットではNIntegrateが ![]() 付近の第2の山形の頂上付近で活発な計算を実行しているのが分かる.NIntegrateは
付近の第2の山形の頂上付近で活発な計算を実行しているのが分かる.NIntegrateは ![]() 付近の積分されない山形付近ではあまり計算を行っていない.
付近の積分されない山形付近ではあまり計算を行っていない.
上記の誤差は領域![]() に対して割り当てられた誤差推定なので,デフォルトの目標精度のNIntegrateではそれ以上の積分調整のためにそれを選ぶことはない.
に対して割り当てられた誤差推定なので,デフォルトの目標精度のNIntegrateではそれ以上の積分調整のためにそれを選ぶことはない.
位相誤差
ここでは積分則が,積分推定の実際の誤差を過小評価・過大評価する理由を説明する.同様の説明が[LynKag76]でもされている.
(NIntegrateはより高い目標精度に対して正しい結果を与える.)
積分則 ![]() が規則
が規則 ![]() に埋め込まれているとする.偶然積分推定
に埋め込まれているとする.偶然積分推定 ![]() (ここで
(ここで ![]() )の誤差推定
)の誤差推定![]() が厳密な誤差
が厳密な誤差![]() と比べて小さすぎることがある.
と比べて小さすぎることがある.
上のプロットで,青は推定誤差![]() を表している.実際の誤差
を表している.実際の誤差![]() は赤で表してある.
は赤で表してある.
一次元積分則は,規則の横座標およびその被積分関数値にフィットする多項式の積分の結果と見ることができる.さらにf[x,λ,μ]の積分に対して実際にフィットする多項式を見ようとすることもできる.
下のプロットでは,関数f[x,λ,μ]が赤で,ガウス多項式が青で,ガウス・クロンロッド多項式が紫で表示されており,ガウスサンプル点が黒い点,ガウス・クロンロッドサンプル点が赤い点になっている.
f[x,0.415,1.25]の頂上が2つの横座標のほぼ半分のところにあるため,その近似は過小評価される.
逆に,f[x,0.53,1.25]の頂上は横座標のほぼどちらかとなっているため,近似は過大評価となる.