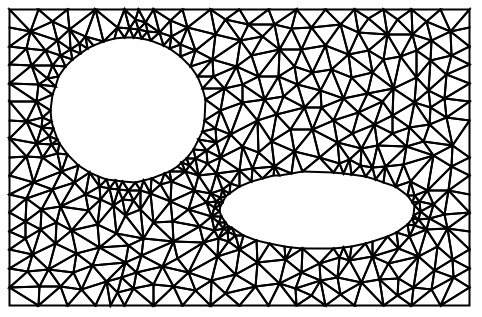
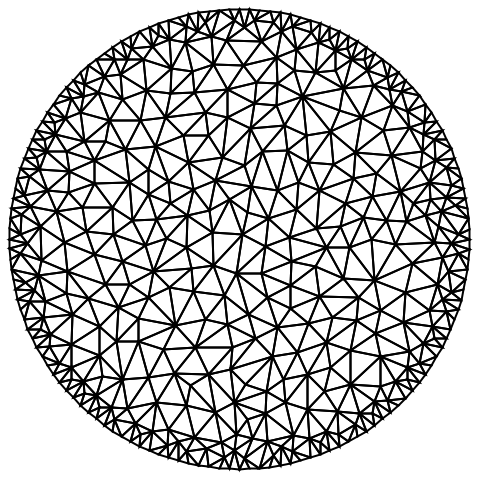
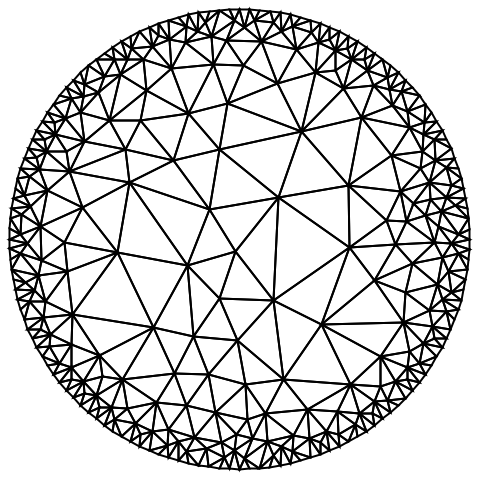
ToElementMesh
ToElementMesh[r]
領域 r からElementMeshオブジェクトを生成する.
ToElementMesh[r,{{xmin,xmax},…}]
境界ボックス![]() に制約された領域 r からのElementMeshオブジェクトを生成する.
に制約された領域 r からのElementMeshオブジェクトを生成する.
ToElementMesh[rules]
座標と要素を指定する rules の集合からElementMeshオブジェクトを生成する.
ToElementMesh[emesh]
既存のElementMesh,MeshRegion,BoundaryMeshRegionのいずれかから,新しいElementMeshオブジェクトを生成する.
詳細とオプション
- ToElementMesh[r]は,記号的である可能性のある領域 r を近似するElementMeshオブジェクトを生成する.
- 領域 r の指定には,幾何学領域とImplicitRegionによって説明されるオブジェクトが含まれる.
- 領域 r は,ConstantRegionQがTrueを与える定数領域でなければならない.
- 領域 r の近似を生成するには,ToElementMeshはまずToBoundaryMeshを呼び出す.
- ToElementMesh[rules]では,rules は以下の順序で与えられなければならない.
-
"Coordinates"->{c1,c2,…} 座標が c1,c2,…になるように指定する必要がある "MeshElements"->{e1,…} メッシュの要素が e1,…になるように指定する必要がある "BoundaryElements"->{b1,…} メッシュの境界要素が b1,…になるように指定する(必須ではない) "PointElements"->{p1,…} メッシュの点要素が p1,…になるように指定する(必須ではない) - 1D要素メッシュでは,"MeshElements"はLineElementである."BoundaryElements"と"PointElements"は,指定されると,PointElementである.
- 2D要素メッシュでは,"MeshElements"は,TriangleElementでもQuadElementでもよい."BoundaryElements"は,指定されると,LineElementであり,"PointElements"はPointElementである.
- 3D要素メッシュでは,"MeshElements"は,TetrahedronElementでもHexahedronElementでもよい."BoundaryElements"は,指定されると,TriangleElementとQuadElementであり,"PointElements"は PointElementである.
- ToElementMeshには,ToBoundaryMeshのオプションに,以下を加えたものが使える.
-
"CheckQuality" Automatic 品質評価を計算する "ElementMeshGenerator" Automatic ElementMeshオブジェクトを境界のElementMeshオブジェクトから生成する関数 "ImproveBoundaryPosition" Automatic 境界ノードの位置を改善する "MeshElementBlocks" 1 メッシュ要素のブロックの数 "MeshElementConstraint" Automatic メッシュ要素の追加の制約条件 "MeshElementType" Automatic メッシュの入力に使われるメッシュタイプ "MeshOrder" Automatic 要素メッシュの次数 MeshQualityGoal Automatic メッシュ要素の目標品質を指定する MeshRefinementFunction Automatic 2Dと3Dの要素の調整を制御する "NodeReordering" Automatic ノードを並び替えて,最小のバンド幅の行列を生成する "SteinerPoints" Automatic Steinerの点の挿入を制御する "RegionMarker" None 領域マーカーを指定する - ToElementMeshのオプションのいずれかを指定することによって,さまざまな方法で,ToElementMesh[emesh,opts]を使ってElementMeshオブジェクト emesh を修正することができる.
- ToElementMeshがElementMeshを生成できない場合には,$Failedが返される.
- EmptyRegionに対してToElementMeshを呼び出すと,EmptyRegionが返される.
- ToElementMeshに与えられるオプションは,"MeshOptions"を指定することによってNDSolveに与えることができる. »
- NDSolveおよび関連の関数からToElementMeshのオプションを設定することについては,有限要素のためのNDSolveオプションに説明がある.
例題
すべて開くすべて閉じる例 (4)基本的な使用例
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-btfg05
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-w7pxg
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-5jg3pt
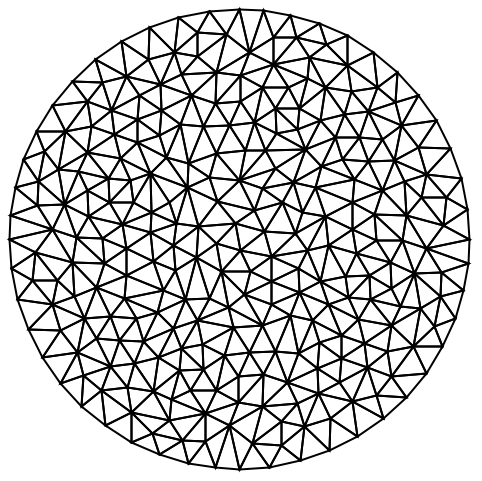
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-2ou2vk
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-ji2kjl

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-2eppju
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-2ouu4a


https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-x5k0lv
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-e0b8zi
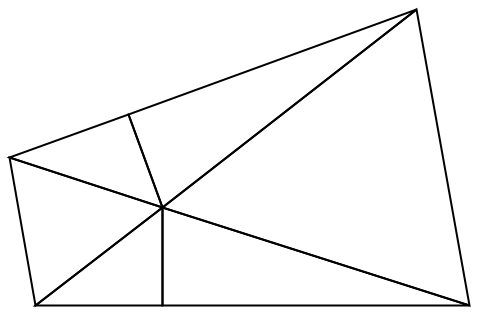
スコープ (29)標準的な使用例のスコープの概要
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-m7p2t4
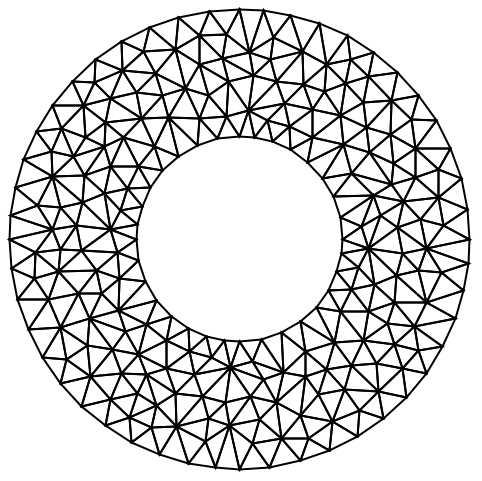
BooleanRegionを使って,2つの円の間の領域にメッシュを生成する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-lwdm3i
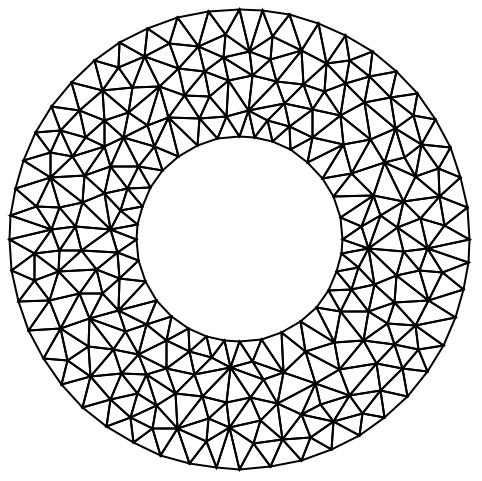
ImplicitRegionを明示的な境界ボックスで変換する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-2kh7pb

RegionDistanceから計算されたImplicitRegionを明示的な境界ボックスで変換する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-sm3dtq
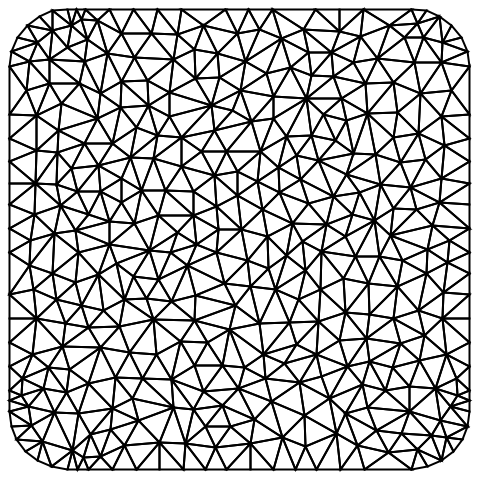
GraphicsComplexを要素メッシュに変換する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-g4smlq
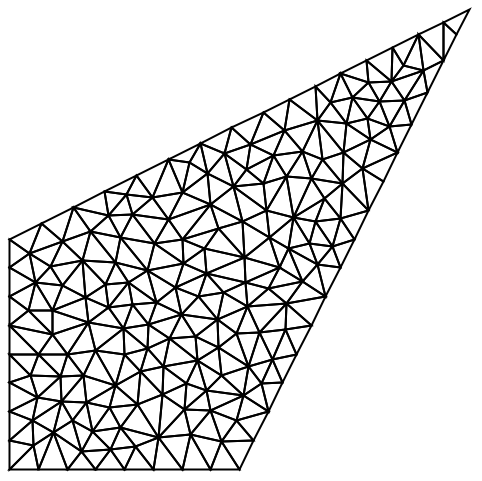
TransformedRegionを要素メッシュに変換する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-xtaym7
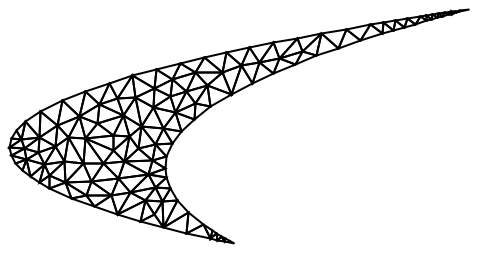
3DのBallを要素メッシュに変換する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-1c5elf
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-g3jilb
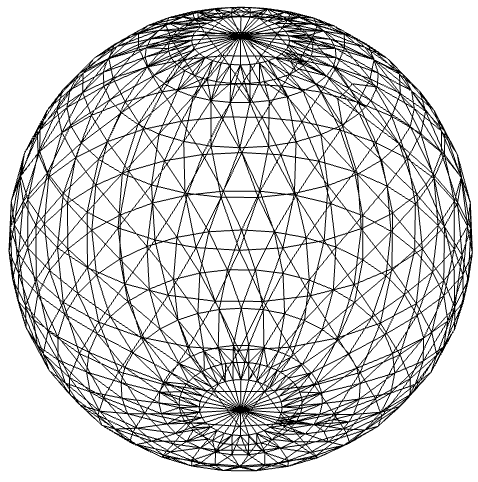
3DのGraphicsComplexを要素メッシュに変換する:

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-4w1oa0
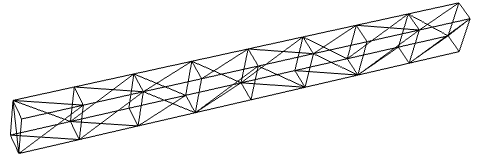
3DのImplicitRegionからメッシュを作成する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-n4ihq3
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-nrhzsj
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-si39ck

3DのBooleanRegionからメッシュを作成する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-u9d32p
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-nax62y
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-jde8m9
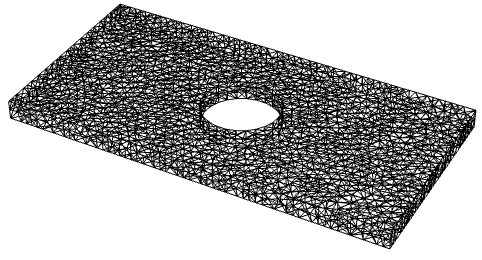
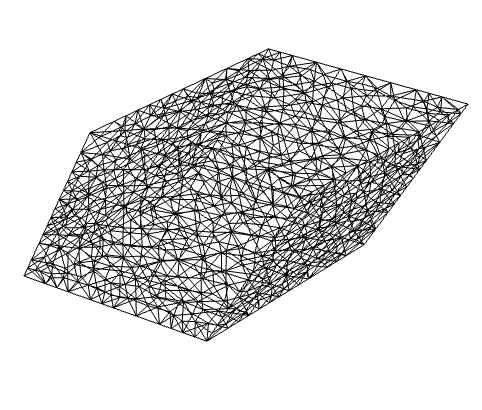
3DのTransformedRegionを要素メッシュに変換する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-vggjx4
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-2j136o
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-s54ezt

点集合については,ToElementMeshはドロネー図を返す:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-tgvxme
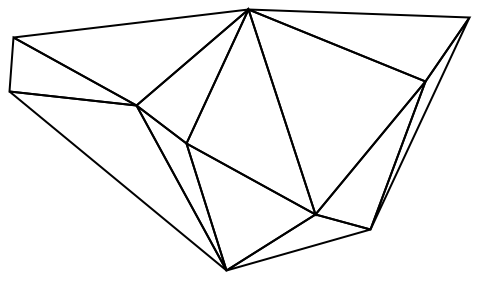
1Dの線分要素メッシュ (3)
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-w8k11y
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-nqrt8z
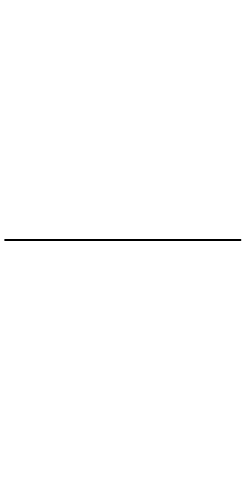
領域の穴を含む1DのElementMeshをImplicitRegionから作成する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-7s4yuq
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-jb5xd3
1DのElementMeshからElementMeshRegionProductを作成する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-myc2sk

2Dの三角要素メッシュ (2)

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-qypolg
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-jj66em
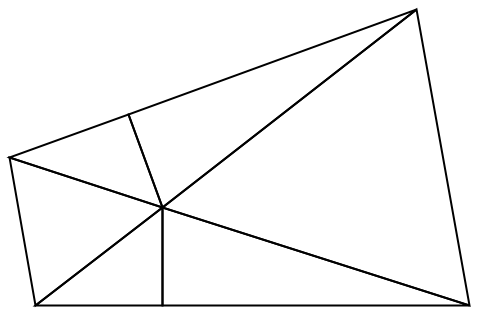
2DのElementMeshと1DのElementMeshからElementMeshRegionProductを作成する:
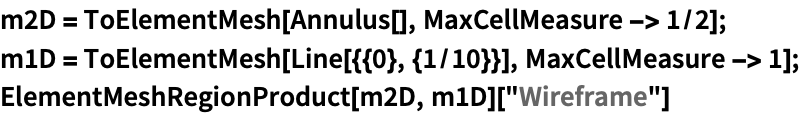
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-xu6338
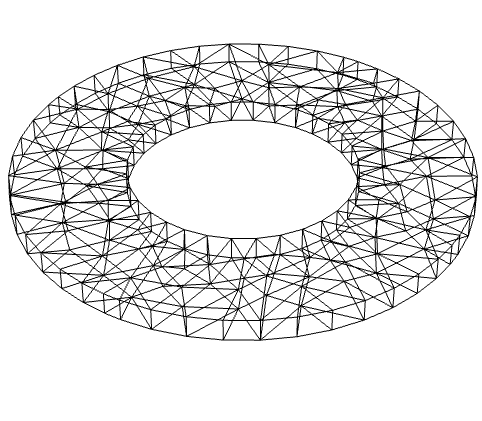
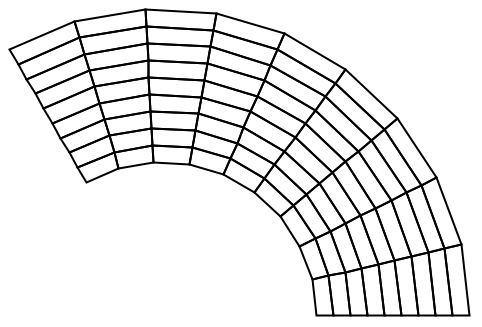
2Dのクワッド要素メッシュ (2)

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-hjamqt
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-2hxsp2
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-5lagaz

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-z21o4g
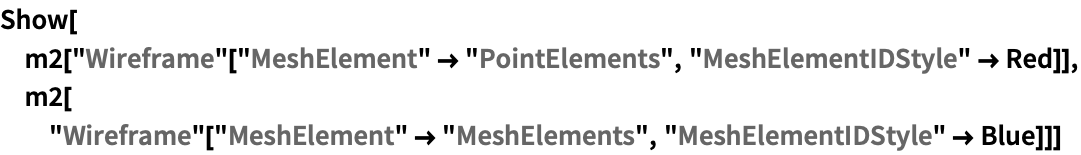
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-6cqk5v
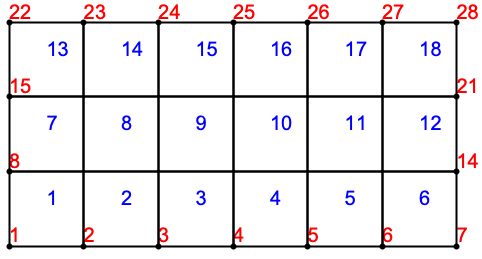
2Dの複合要素タイプのメッシュ (1)
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-y7m4zj

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-5ksxcf
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-2nsyfc
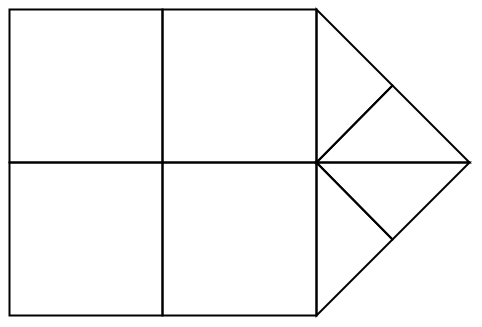
2Dの高次要素メッシュ (1)

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-e3jncq
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-pderxe
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-krr4q8

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-ibezk2

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-qaee0c
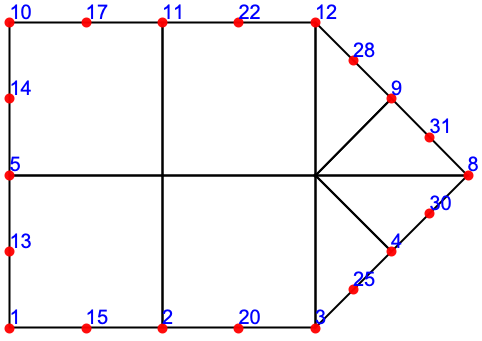
3Dの四面体要素メッシュ (1)
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-hnrx9r
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-vf52b6

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-bjnnx9
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-fr0s8d
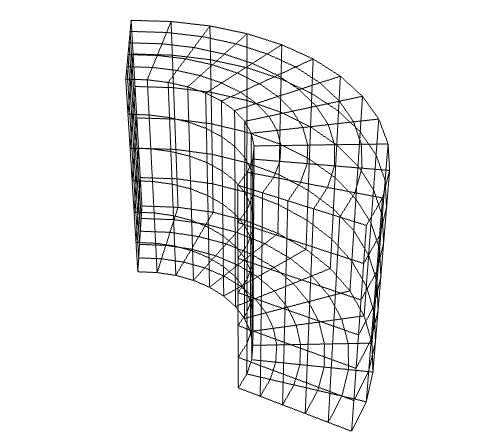
3Dの六面体要素メッシュ (1)

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-u38ajg
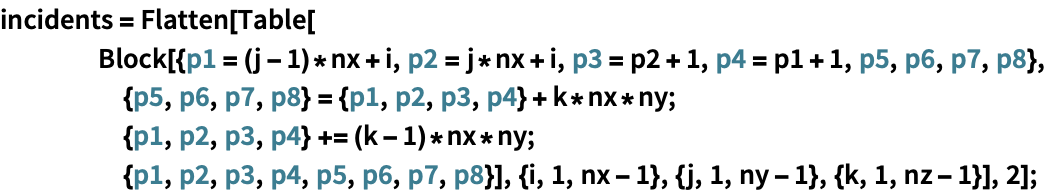
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-14vq8h
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-ronku0
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-9fvicm
画像 (2)
領域マーカー (1)
領域マーカーは,領域内の複数のものを指定するのに便利であり,「要素メッシュの生成」の「マーカー」セクションに詳しく説明されている.

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-mzunnb

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-5ktme9
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-xb9wla
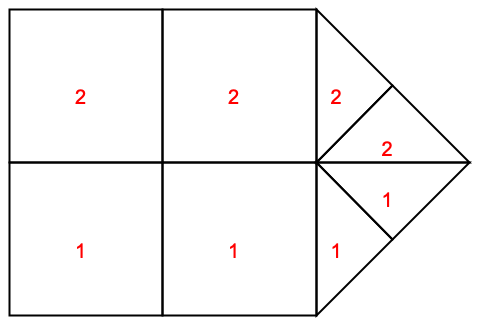
境界マーカー (1)
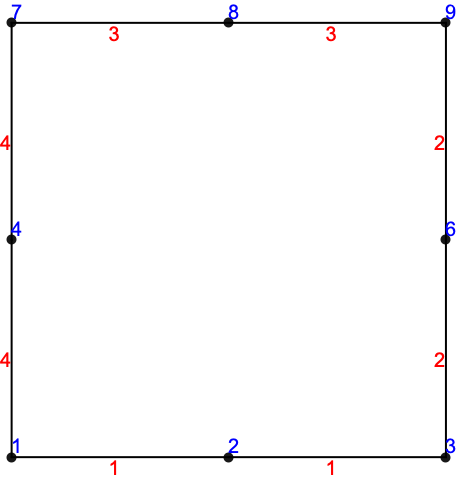
境界マーカーは,領域境界上でNeumannValueを指定するのに便利であり,「要素メッシュの生成」の「マーカー」セクションに詳しく説明されている.
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-lutdgp
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-5whk9r
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-e92dz5
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-vvjlqb
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-q535wt
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-71i4k2
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-o6oxyq
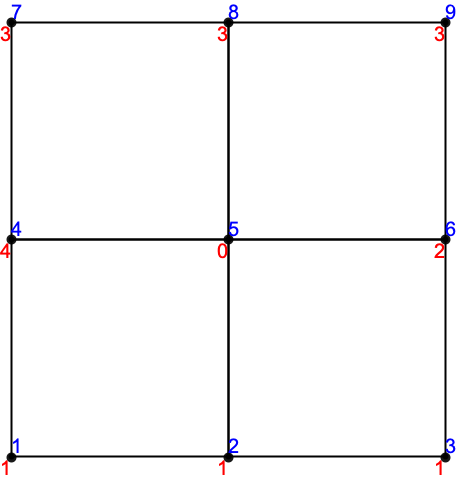
点マーカー (1)
点マーカーは,領域境界上でDirichletConditionを指定するのに便利であり,「要素メッシュの生成」の「マーカー」セクションに詳しく説明されている.
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-e2m279
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-staraw
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-wzu9y7

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-z266rb
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-67hvnp
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-8zjkhf

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-4yyppa
オプション (41)各オプションの一般的な値と機能
"BoundaryMarkerFunction" (2)
境界マーカーは,領域境界上でNeumannValueを指定するのに便利であり,「要素メッシュの生成」の「マーカー」セクションに詳しく説明されている.
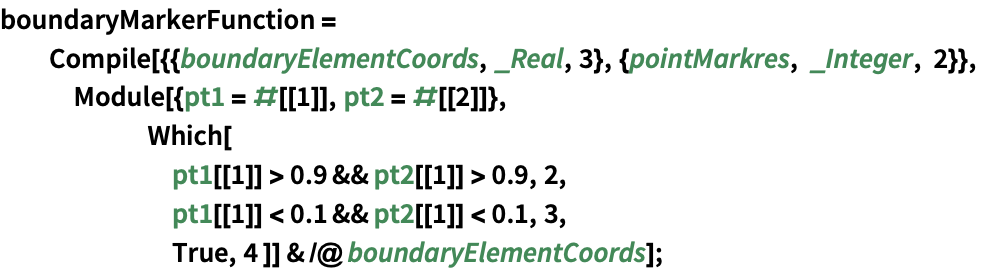
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-83pijl

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-gize4e

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-u9eiw5
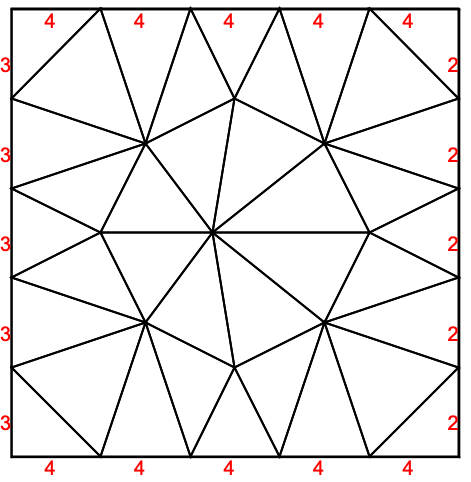
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-fdp0nh
"PointElementMarkers"も計算された場合には,それらは,"BoundaryMarkerFunction"に与えられる関数の第2引数としてアクセス可能である.

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-2d98tv

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-6vfjsx

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-tbqtd0
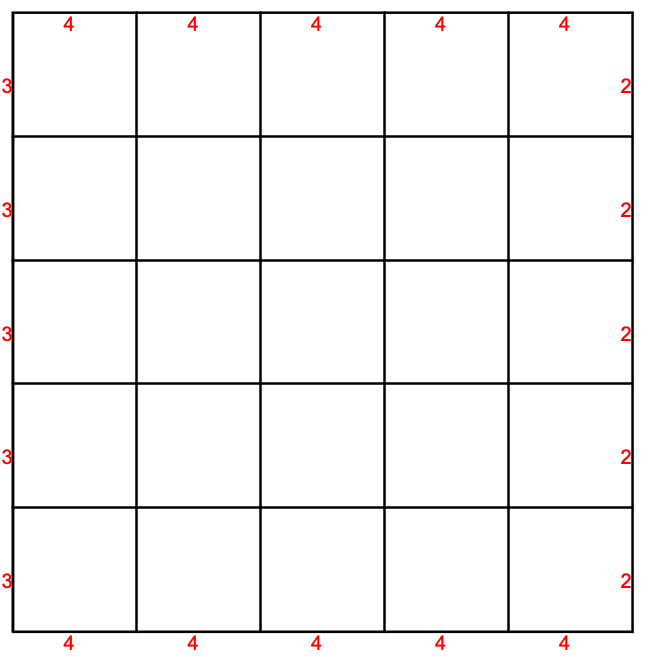
"BoundaryMeshGenerator" (2)
"Continuation"メソッドは,多くの場合にコーナー,尖点,急な変化をかなりうまく処理することができる曲線継続法を使う:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-4n5a3t
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-vmcdyp

"RegionPlot"メソッドは,RegionPlotからの出力を改善することに基づいており,より速い場合もある:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-pa1601
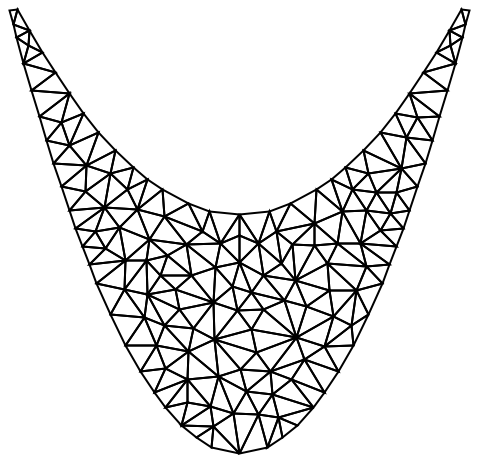
"BoundaryMeshGenerator"オプションの詳細は,ToBoundaryMeshのページを参照されたい.
"OpenCascade"の境界メッシュ生成器は,Graphics3Dプリミティブからなる3DのBooleanRegion式に使うのに適している.

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-qy0jgz
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-zrcwtn

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-5mvwlv
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-c41p8x
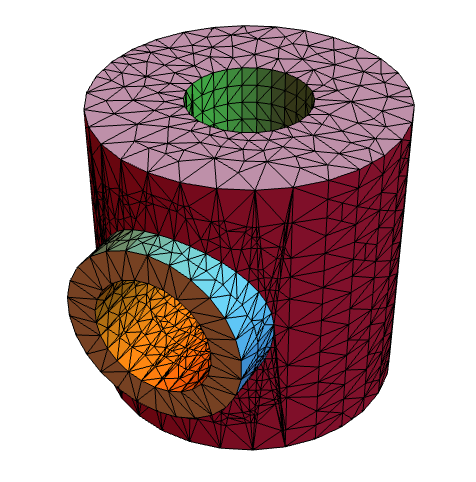
"ElementMeshGenerator" (1)

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-btyilf
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-1zkrma
カスタムのメッシュ生成器に与えられた数値領域には"BoundaryMesh"が含まれる.メッシュ生成器のインターフェースが記号表現を使うので外部メッシュ生成器へのインターフェースに境界メッシュ表現が必要ないという場合は,"BoundaryMeshGenerator"->Noneと設定することによって,境界メッシュの生成を行わないようにすることができる.
"ImproveBoundaryPosition" (1)
ImplicitRegionの近似は,一般に厳密ではない."ImproveBoundaryPosition"オプションは,境界ノードの位置を改善することを助ける:

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-18d3lh
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-tra0wf
境界ノードの平方の総和は,必ずしもすべて値1にあるわけではない:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-3r6saz

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-mkgz2b
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-z9r098
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-txjzfe
"ImproveBoundaryPosition"オプションがFalseに設定されている場合には,二次要素は領域の曲線部分の境界上の中間ノードを持たない.
"IncludePoints" (3)
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-0kim8w
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-civoaz
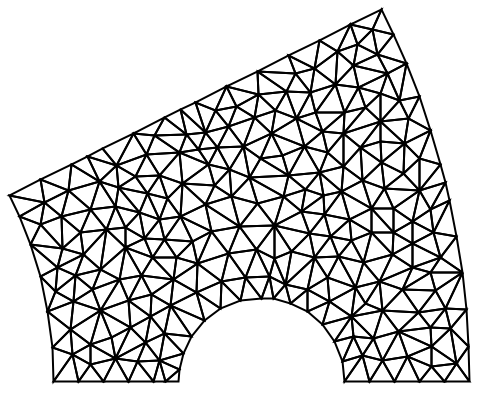
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-bgzudk
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-o17pk9
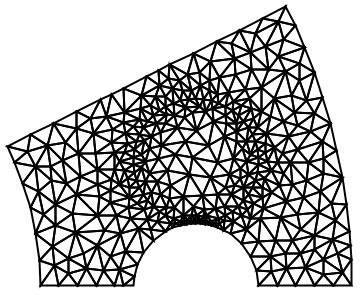
"IncludePoints"を使って加えられた点は,DirichletConditionで使える.さらに,DirichletConditionの述部がTrueであれば,境界条件は加えられた点において有効となる.
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-by2k1o
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-qnyb4
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-70fa1s
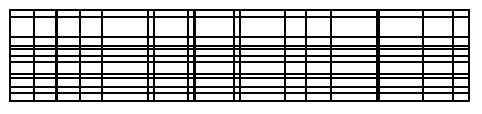
"IncludePoints"は,ToBoundaryMeshのオプションであり,ToElementMeshはオプションを渡す.しかしこのことは,ToElementMeshに境界ElementMeshが提示された場合に,その要求を満たすことができないことを意味する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-kgv0f
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-zisg7
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-9siw82
点{0,0}は含まれていない.この問題を解決する策として,ToBoundaryMeshの呼出し中に"IncludePoints"を指定するか,ToElementMeshを呼び出す際に記号的領域を利用するかの方法がある.
ToBoundaryMeshの呼出し中に"IncludePoints"を使う:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-ei4qeb
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-mvgdz8
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-u2f5lc
あるいは,ToElementMeshの呼出しに記号的領域を使う:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-maycwv
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-klp34s
"MaxBoundaryCellMeasure" (2)
"MaxCellMeasure" (4)
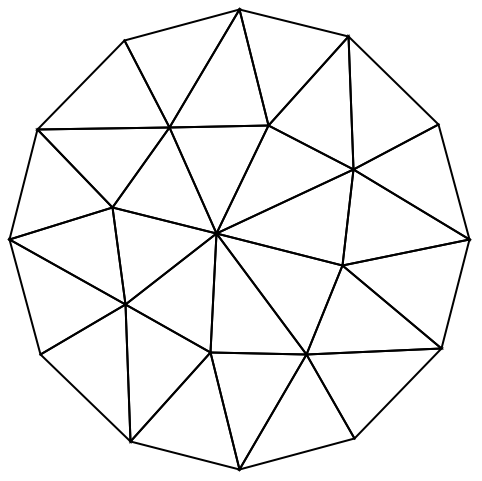
MaxCellMeasure->m で,セルの大きさが選ばれ,境界セルの大きさが埋込み次元内の高品質セルに適切なものに設定される:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-kbjrf2
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-njdxry
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-8zr5iw
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-48x2y
最大セルの大きさは,線形要素に働く.曲線境界のより高次のメッシュの場合には,実際のセルの大きさがより大きくなることがある:
特定の長さは,MaxCellMeasure->{"Length"->len}で指定することができる:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-twuk4t

特定の長さと範囲がMaxCellMeasure->{"Length"->len,"Area"->area}を使って指定される場合には,より厳しい必要条件が満たされる:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-zdr2at

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-ugrvba
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-o3b5a6

"MeshElementBlocks" (1)
"MeshElementConstraint" (2)
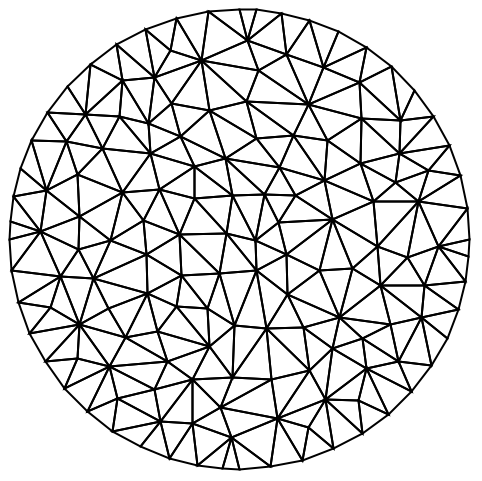
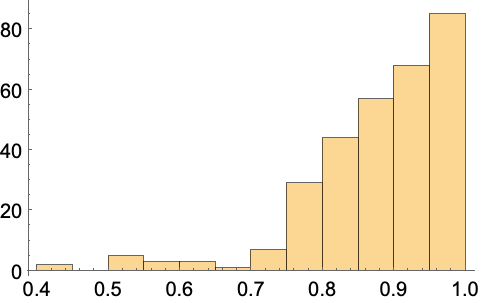
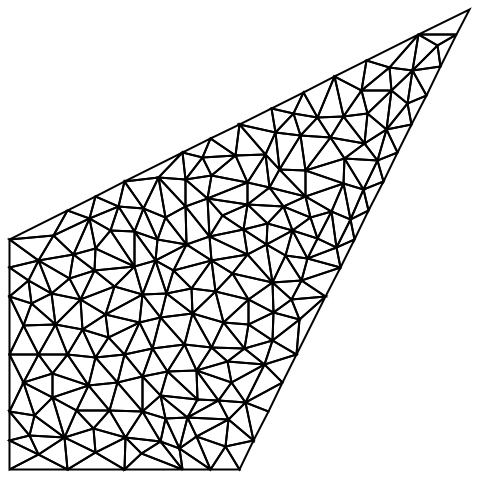
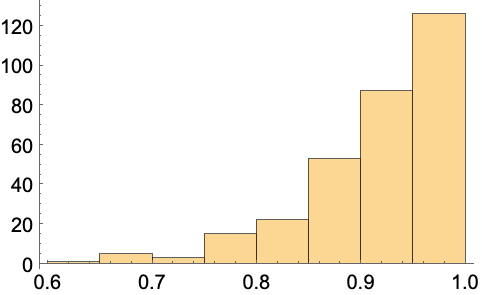
TriangleElementに基づく二次元のメッシュについては,最小の三角角度は,"MeshElementConstraint"オプションを通して指定できる:

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-zo87dq
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-n449c2
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-hapmcn
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-dqru5l
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-jda7d
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-de94ii
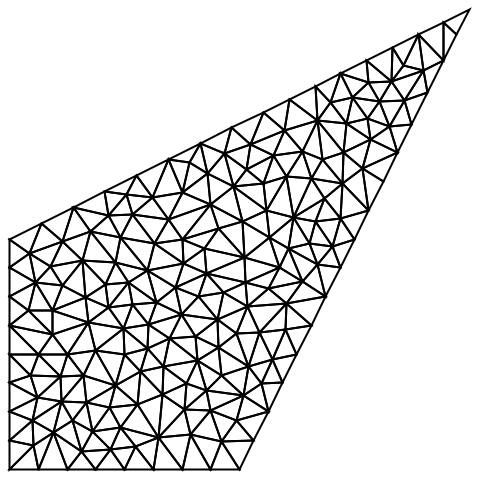
指定された最小角度は,33度より小さくなければならない.理論的には,アルゴリズムは,22.7度より小さい最小角度を確実になくすことになっているが,実際には,33度までの最小角度でも成功することがしばしばある.
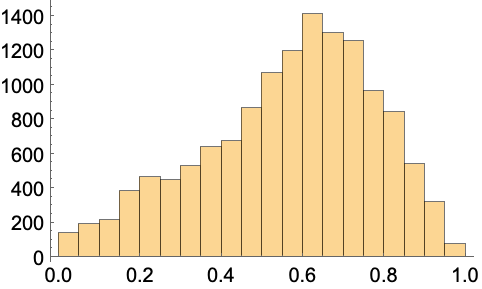
三次元のTetrahedronElementメッシュについては,四面体半径の辺の長さに対する最小割合は,"MeshElementConstraint"オプションを使って指定することができる:

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-q5mzk1
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-55au4p
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-0cx3lt
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-5va19b
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-iwnhyu
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-g30881
半径と辺の割合は,![]() より大きくなければならない.理論的には,アルゴリズムは,半径と辺の割合が2である場合には確実になくすことになっているが,実際には半径と辺の割合が
より大きくなければならない.理論的には,アルゴリズムは,半径と辺の割合が2である場合には確実になくすことになっているが,実際には半径と辺の割合が![]() まで下がる場合にもしばしば成功する.
まで下がる場合にもしばしば成功する.
"MeshElementType" (1)
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-kseak8
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-rhrohm

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-7dcfov
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-xsby2m

"MeshOrder" (1)
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-b0wm7
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-j6xq99
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-daqkd4
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-c4nodx
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-magog3
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-038kj7
"MeshOrder"オプションの詳細については,要素メッシュの生成と要素メッシュの可視化のチュートリアルを参照されたい.
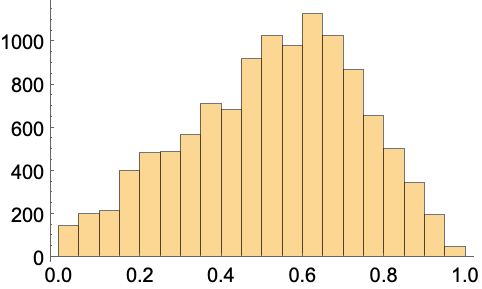
"MeshQualityGoal" (1)
品質の値 ![]() は,正規のメッシュ要素については
は,正規のメッシュ要素については ![]() ,変化したメッシュ要素については
,変化したメッシュ要素については ![]() になるように,計算される:
になるように,計算される:
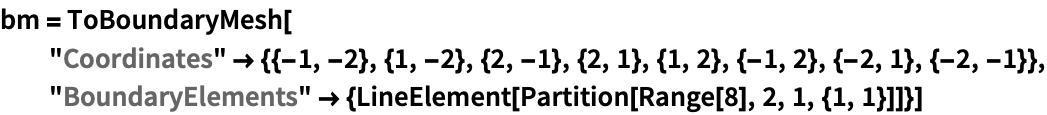
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-8vlu3c
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-dri70u
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-s2ivoy
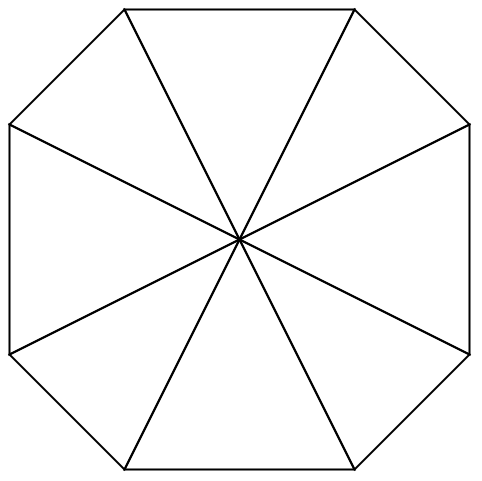
"MeshRefinementFunction" (9)
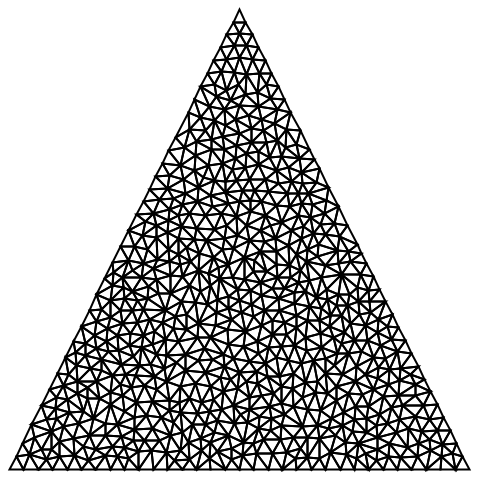
特定の2D三角要素が細分化されなければならない場合に,Trueを返す関数を作成する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-e08tn1
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-qa56b4
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-eke55w
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-vrk2el
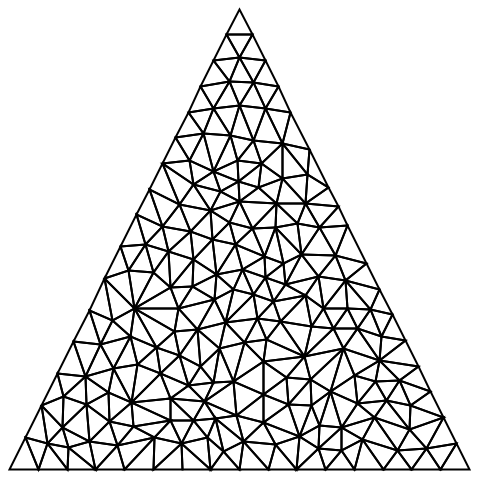
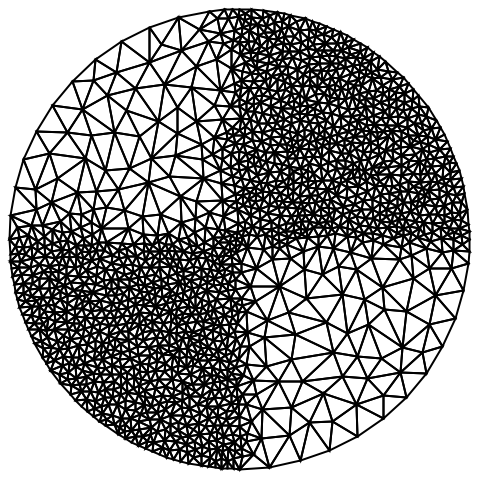
特定の2D三角要素が細分化されなければならない場合に,Trueを返すコンパイルされた関数を作成する:
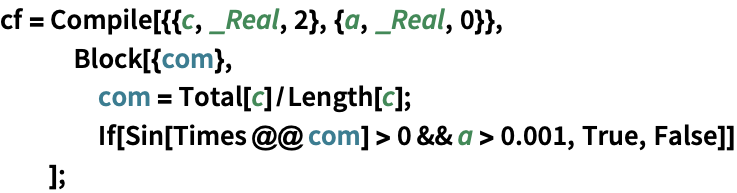
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-cgnoqh
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-fq9z0m
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-8nj5ef
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-u1l68g

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-9c5zll
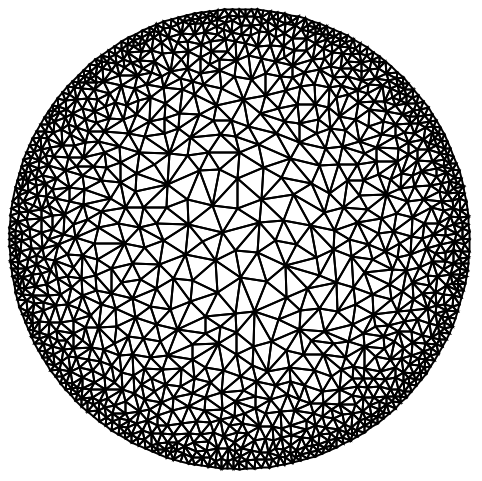
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-jmcojf
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-dq7x5t
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-hh3voj


https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-ldyclj
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-zg6nbv
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-rtscsz


https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-h1nu93
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-4q2un0
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-l6545v
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-kdgrm

特定の2Dの三角形要素が細分化されなければならない場合にTrueを返す関数を作成する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-btvq0j
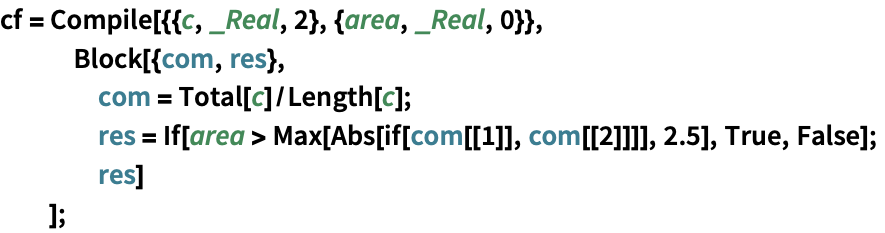
TrueあるいはFalseを返すコンパイルされた関数を作成する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-o3zpyx
コンパイルされた細分化関数で境界メッシュの完全メッシュを作成する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-s48vg4
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-5zzb4d
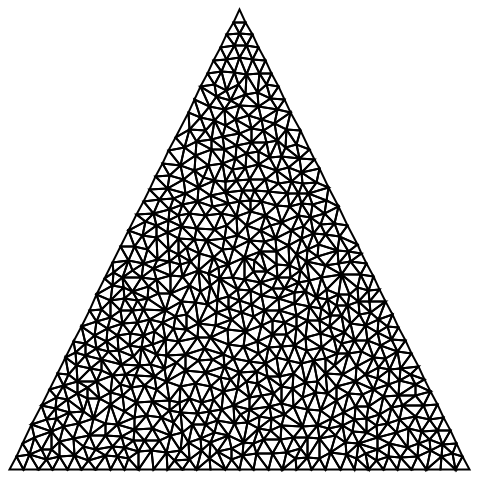
特定の3Dの四面体要素が細分化されなければならない場合には,Trueを返すコンパイルされた関数を作成する:

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-qyfvp7
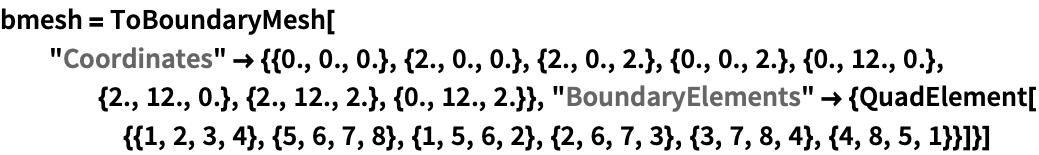
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-4ubngy
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-spqtnw
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-kmwfxk
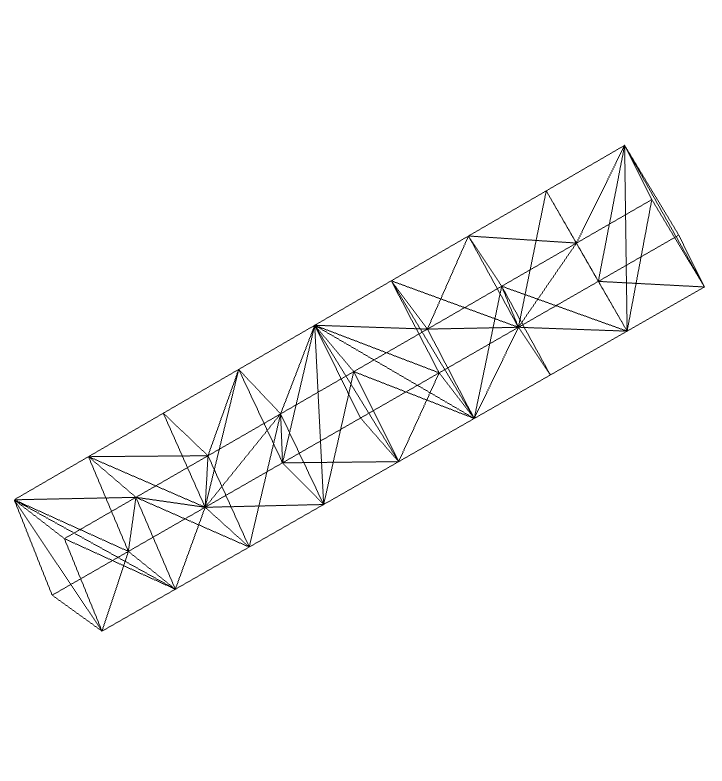
1Dでは,DiscretizeRegionを使って細分化を行う:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-u5sm8b
"NodeReordering" (2)
領域からElementMeshを作成する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-xg23b7
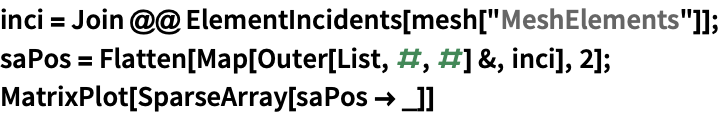
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-lyjmt7
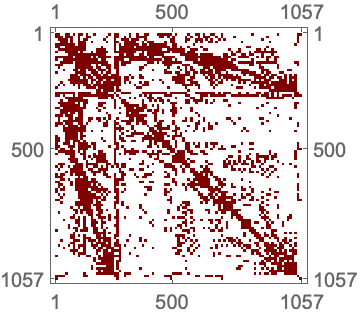
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-7eiu9r

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-m9jg0b
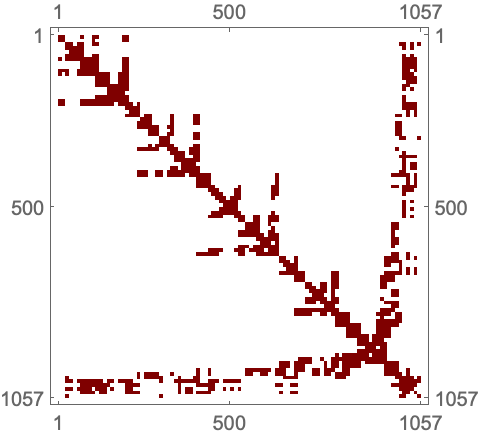
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-g1h6ay

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-ckk2o8
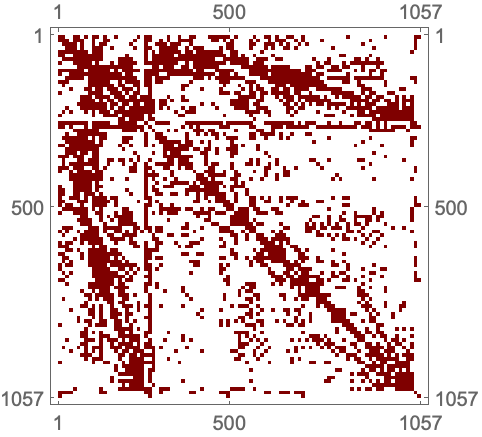
"PointMarkers" (1)
点マーカーは,領域境界上でDirichletConditionを指定するのに役立つものである.「要素メッシュの生成」の「マーカー」.セクションに詳しい説明がある.
メッシュに点マーカーを設定する方法はいくつかある.その一つとして,境界マーカーから点マーカーを得る方法がある.
領域にメッシュを掛け,境界マーカーから点マーカーを推測する:

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-26m44x
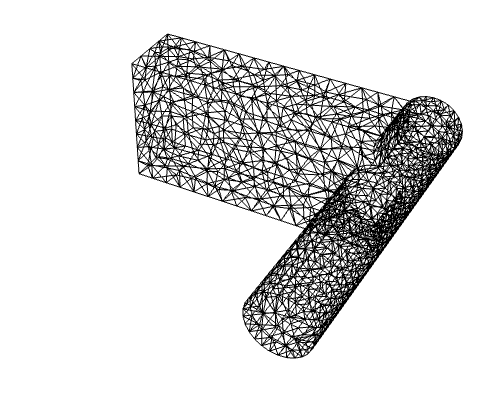

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-14j39u
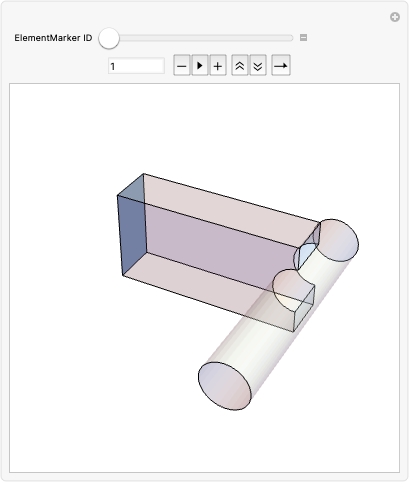
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-6k1xon

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-1uadmv
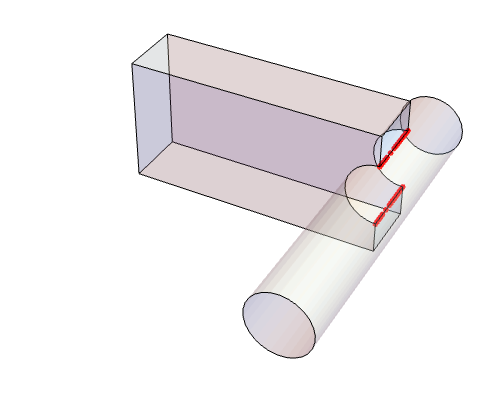
すべての曲面に繋がっている点のみを考慮するような交点を求める.IDが7の境界マーカーは,大きな円柱の曲面である:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-drffu8
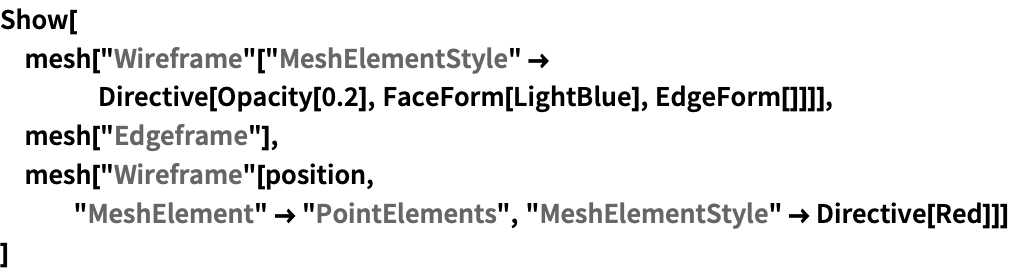
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-m5oris
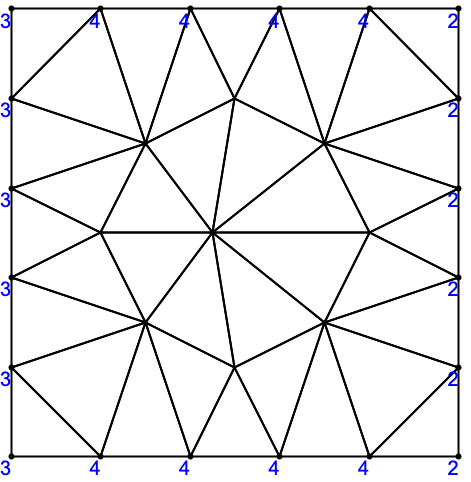
"PointMarkerFunction" (1)
点マーカーは,領域境界上でDirichletConditionを指定するのに便利であり,「要素メッシュの生成」の「マーカー」セクションに詳しく説明されている.

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-7aezk3

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-btpy3b

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-ey7o77
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-wf20dg
二次メッシュの中間ノードの点マーカーの値は,境界要素マーカーから導き出される.ここでは何も与えられていないので,値は無作為である:

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-g15l8b

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-kidlpi
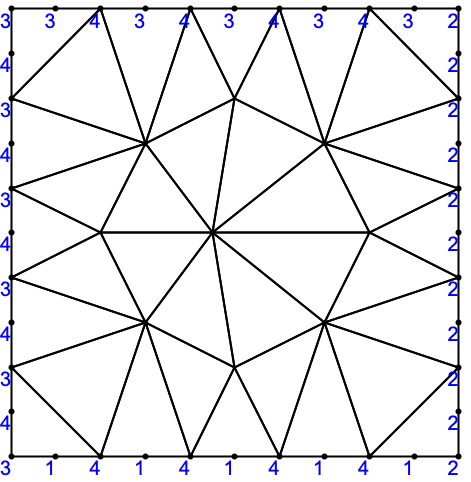
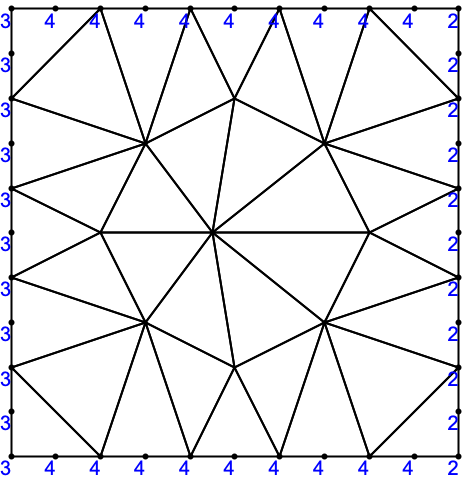
"BoundaryMarkerFunction"も計算された場合には,中間ノードは,境界要素マーカーから導き出された値を持つ:

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-2gerbp

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-lwu1o1

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-wc04mc
"RegionHoles" (4)

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-rcympe

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-f1a5gk

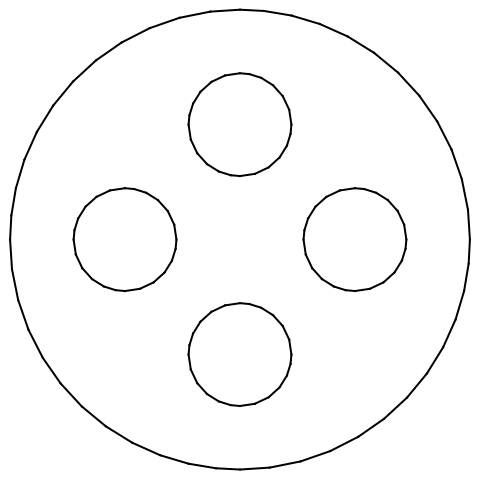
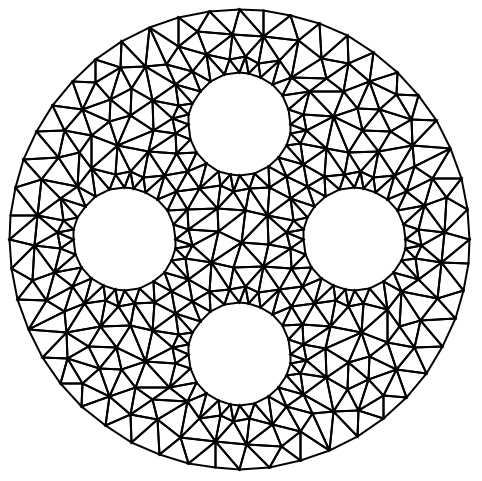
内部を領域の穴として指定して,境界メッシュから完全なメッシュを作成する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-23ivr8

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-lf9d5z

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-44w0ix

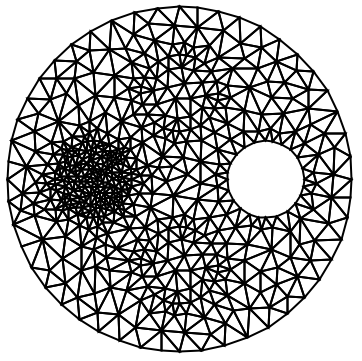
穴の領域の座標を明示的に与えないことによって,穴ではない領域にメッシュを掛ける:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-i6vklo

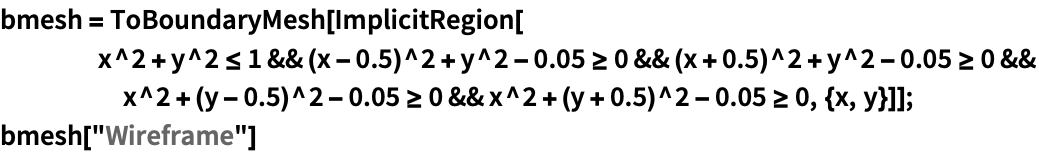
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-itci3v
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-pwv62k
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-ip8l2k
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-1eqw2c
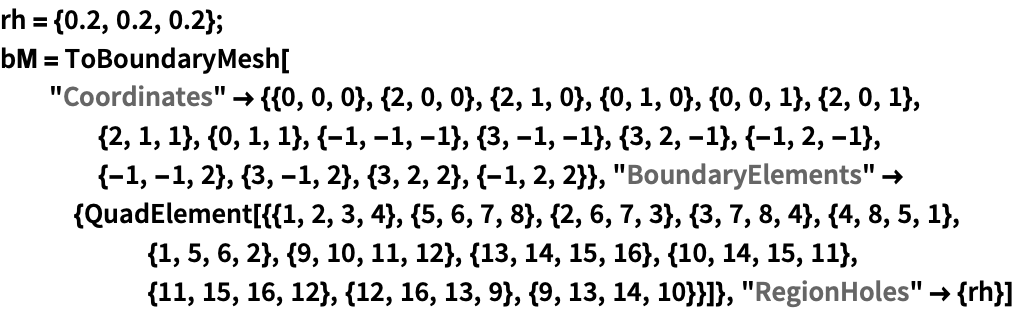
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-n6sdx9
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-8a86fx
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-0p0wyk

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-o50s8u
"RegionMarker" (2)
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-gps8yl
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-8b8ltb

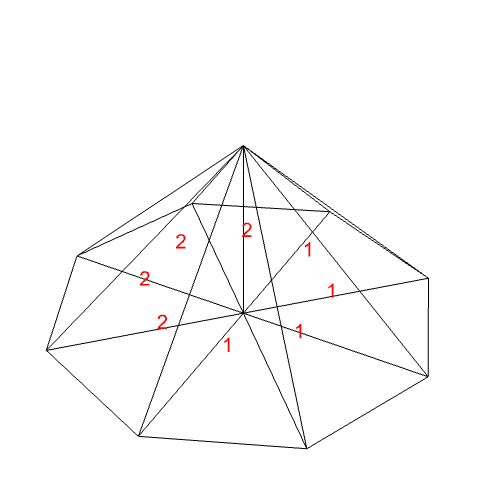
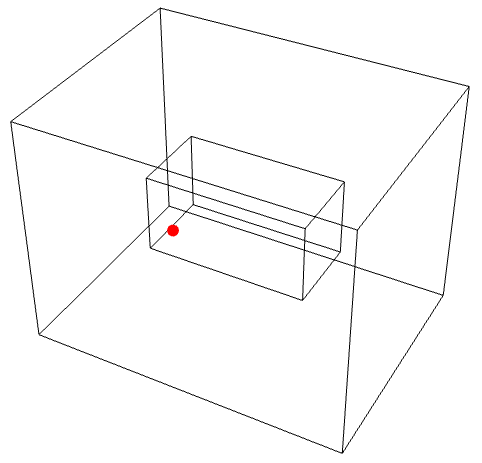
{1/2,3/4}を含む境界要素はマーカー1を,{1/2,1/4}を含む領域はマーカー2を使うべきである:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-9ootmb

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-o7b22y
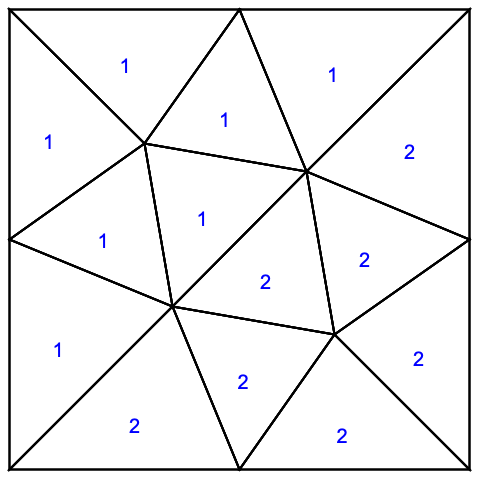
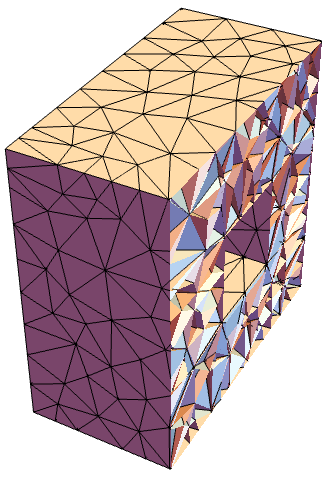
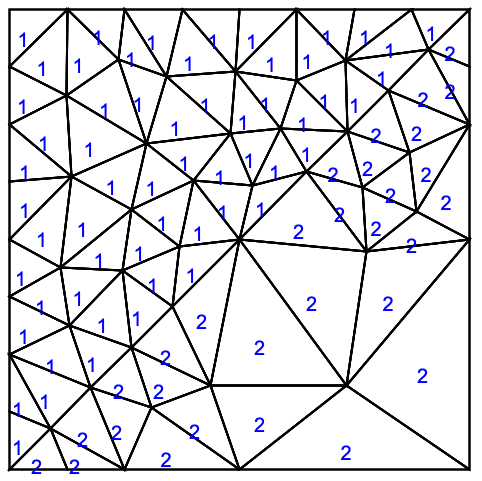
さらに,マーカー1の領域の細分化パラメータがマーカーに与えられる:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-3mm9ao

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-2ro2qs

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-nl83t6
内側の部分領域が別の細分化に従う,完全な要素メッシュを作成する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-cl7io7

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-qaqci1
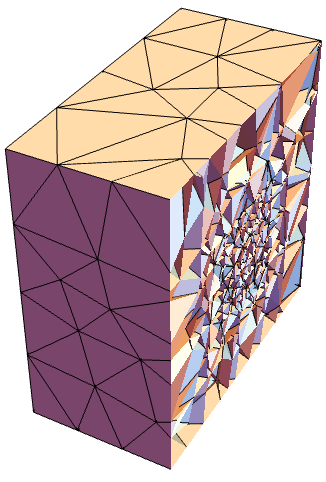
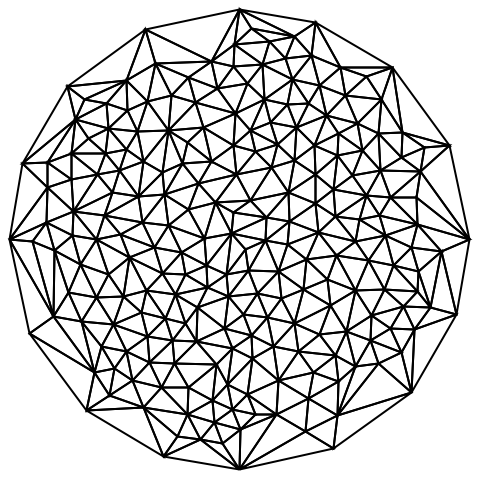
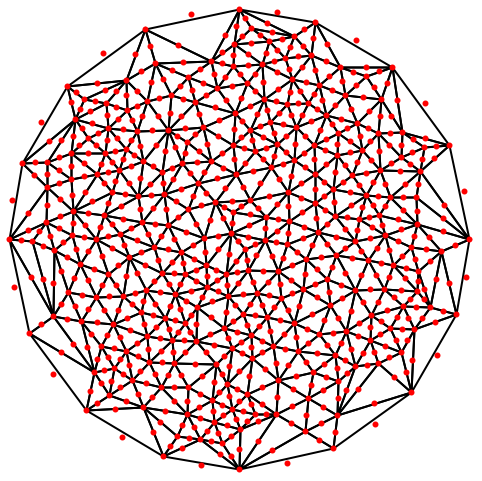
"SteinerPoints" (1)
2Dの三角メッシュについては,Steiner点の挿入が制御できる.この場合には,境界は境界の大きさを守り,それ以上分割を行わない:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-zlz0f

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-0wippp

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-qav2u0
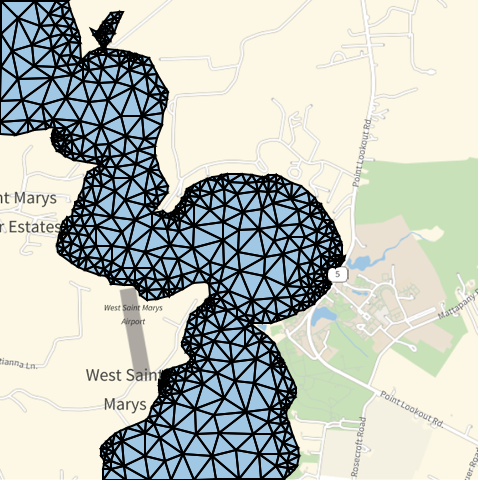
アプリケーション (2)この関数で解くことのできる問題の例
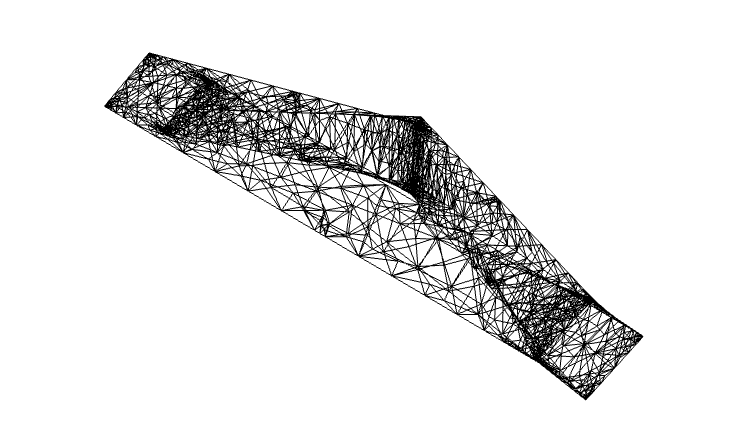
GeoGraphicsから川のElementMeshを作成する:

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-jjm5bj
![]() で2つのネストした半環帯の境界メッシュを生成する.それぞれの環帯は異なる部分領域を表す.1つ目の部分領域は内半径が
で2つのネストした半環帯の境界メッシュを生成する.それぞれの環帯は異なる部分領域を表す.1つ目の部分領域は内半径が ![]() で外半径が
で外半径が ![]() ,2つ目の部分領域は内半径が
,2つ目の部分領域は内半径が ![]() ,外半径が
,外半径が ![]() である.
である.
まず3つの半円盤を作成し,次に3つの部分領域の和を生成し,最後に2つの環帯を作成するために最初の半円盤を内側の穴とする.
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-etpgpj
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-eeho4r
Circleを使って半円盤を作成する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-l3fj4
半円盤の和が作成されると,左の境界は自動的に和から削除される.このため,領域をもう一度繋げるために,線分が作成され,半円盤の和に繋げられる.1つ目の半円盤に穴を開けるために,和を ![]() から
から ![]() まで,および
まで,および ![]() から
から ![]() まで
まで ![]() 方向に繋げ,1つ目の半円盤を脇にのける.
方向に繋げ,1つ目の半円盤を脇にのける.
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-72kt1
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-blal2p
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-bma7fa
RegionMarkerを使って,定義された部分領域で要素メッシュを生成し,メッシュを![]() に限る:
に限る:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-cb7v5q
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-lcti1

特性と関係 (5)この関数の特性および他の関数との関係
ElementMeshは,NDSolveによって返されるInterpolatingFunctionの一部である:
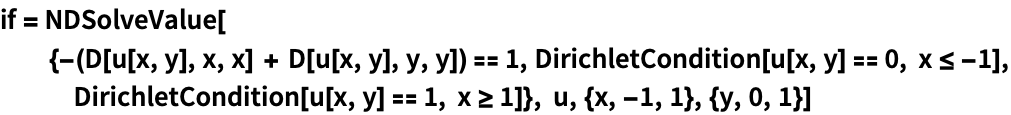
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-ehyiyq
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-xczble
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-522tz4
ElementMeshをNDSolveに渡す:
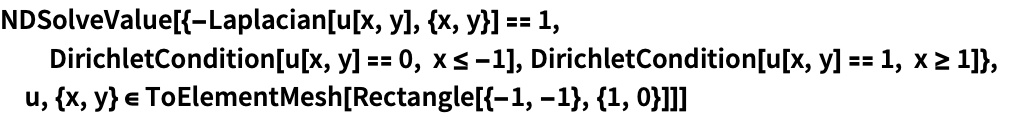
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-l20khm
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-gnxlyf

ToElementMeshのオプションをNDSolveに渡し,定常偏微分方程式を解く:

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-yqowvy
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-kjorkk
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-q17dk3
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-wo44ov
ToElementMeshのオプションをNDSolveに渡し,時間依存の偏微分方程式を解く:to solve a time-dependent PDE:

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-qeclpa

考えられる問題 (11)よく起る問題と予期しない動作
入力の記号的領域に境界がない場合には,デフォルトの![]() からの境界ボックスが各空間方向に想定される:
からの境界ボックスが各空間方向に想定される:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-s7i8l4
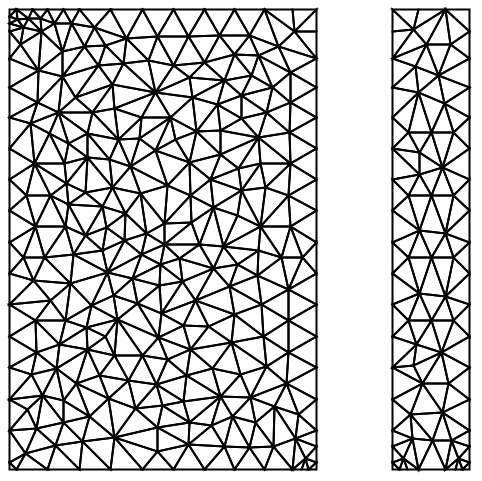
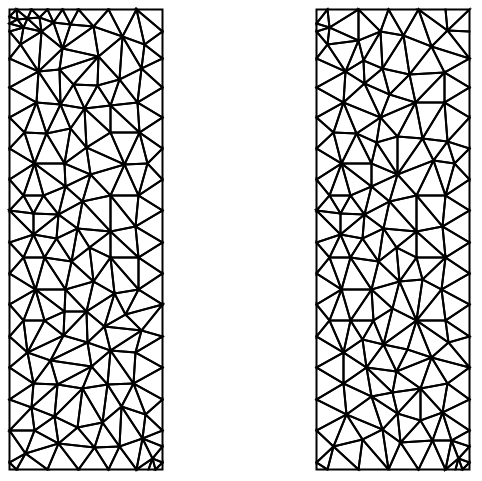
明示的な境界ボックスを指定することによって,デフォルトを無効にできる:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-s68jfd
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-8zcpct

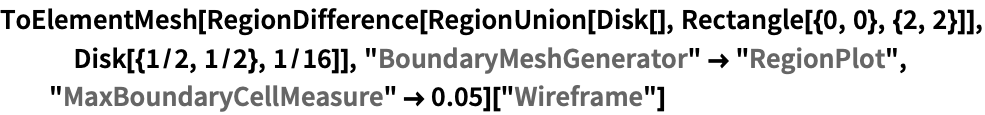
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-faelg
ImplicitRegionでは,指定のない記号パラメータを使うことはできない:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-z5hg5r
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-w9qtph
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-iagqzd
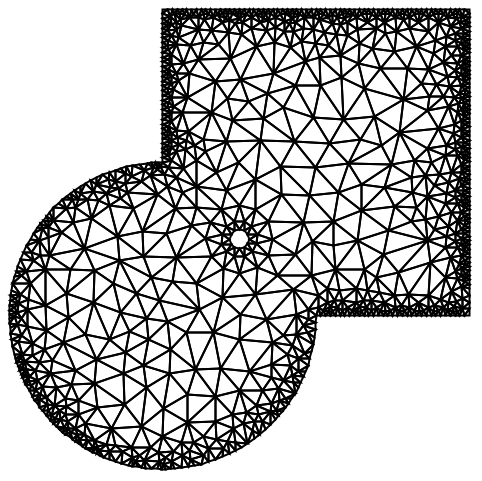
境界ボックスが領域指定と交差する場合には,結果として低品質のメッシュが作成されることがある:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-87i2n7
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-0vw83f
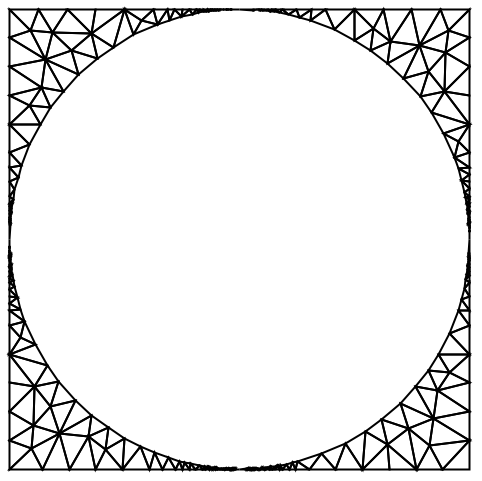
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-s4wkqx
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-8fciod
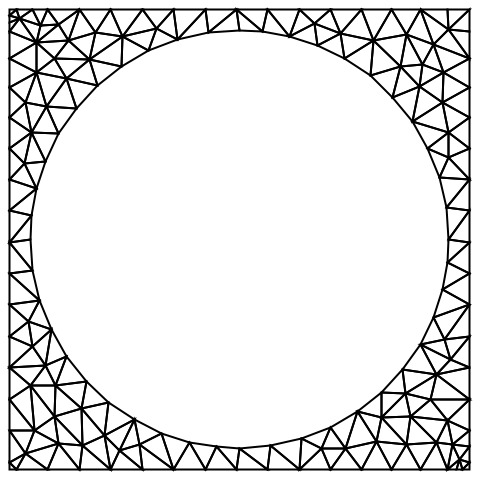
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-zg3v08
ElementMeshのメッシュ要素は,同じ次数のものでなければならない:

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-bsbysc
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-7s7lv5
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-o2zskk

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-18zjo7
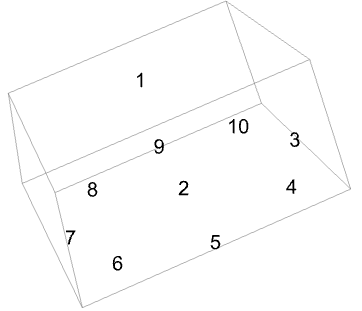
要素インシデントは,反時計回りの順に与えられなければならない:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-9p5bli
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-2np70h

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-k2gsyg
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-po5sq2
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-02kmbn

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-vinig2
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-bgaliu
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-mrwna7

MeshRegionからElementMeshへの変換が,メッシュを直接変換する形で行われるとは限らない:

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-xbbbpl

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-ogwvcj

これは,ToElementMeshが与えられたメッシュのオプションに沿えることができなければならないためである.MeshRegionを生成するのに使われたパラメータを推定し,ToElementMeshオプションが満たされるかどうかを確かめることは不可能である.MeshRegionを直接ElementMeshに変換することが可能な場合もある:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-r3slk0

この場合には,ToGradedMeshとElementMeshRegionProductを使うことによって,ElementMeshを直接生成することが可能である:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-y634m1
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-175y13

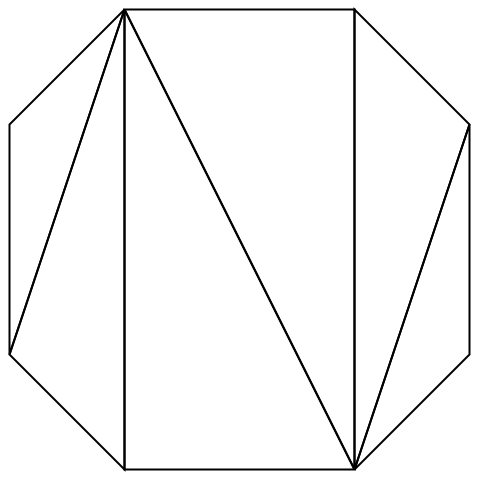
ToElementMeshの引数は規則として指定し,正しい順序("Coordinates","MeshElements"の順序で,次にオプショナルの規則"BoundaryElements"と"PointElements"を加える)で与えなければならない:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-fhsa0t
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-vswvb8
陰的な領域についてのメッシュ生成アルゴリズムの中には,完全には決定性ではなく,同じ入力に対して少し異なるメッシュを返すものもある:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-4817ju
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-xfvq75
おもしろい例題 (3)驚くような使用例や興味深い使用例
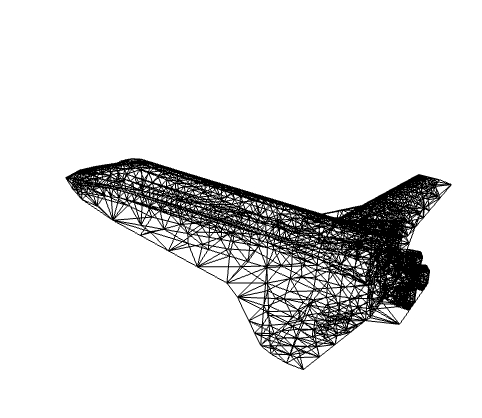
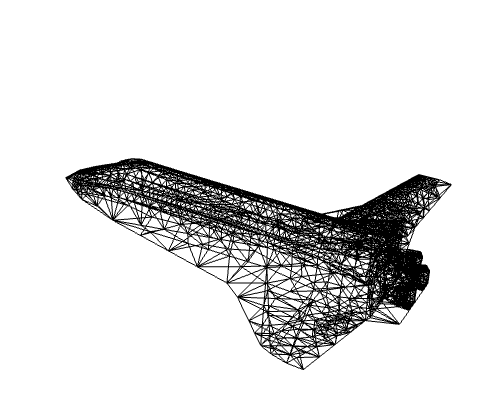
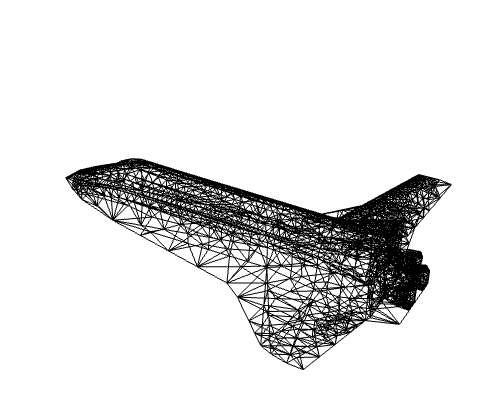
スペースシャトルのオービタをElementMeshに変換する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-uz6lh3
画像を要素メッシュに変換するには,まず,画像を距離関数に変換する:

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-yj81es
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-mnsz6i
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-or4rub


https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-vcenyz
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-0bfvv4
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-r23qpk

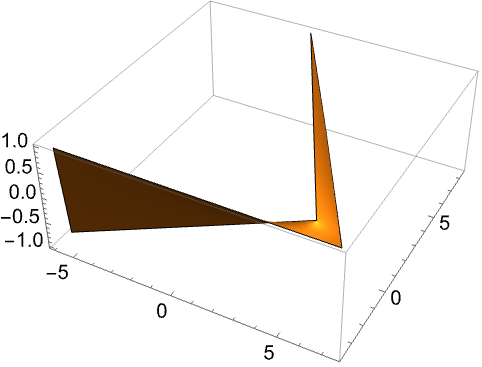
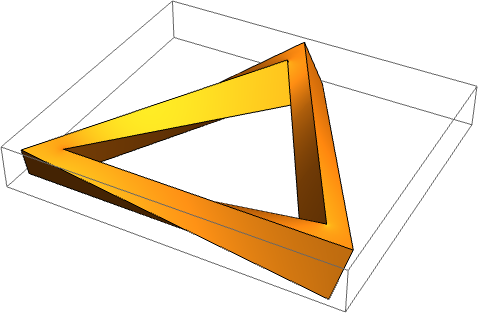
以下の拡張例は,ペンローズの三角形を作成するもので,ラプラス方程式を解くことに基づく.パラメータを指定する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-9mskf
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-kfkg8b
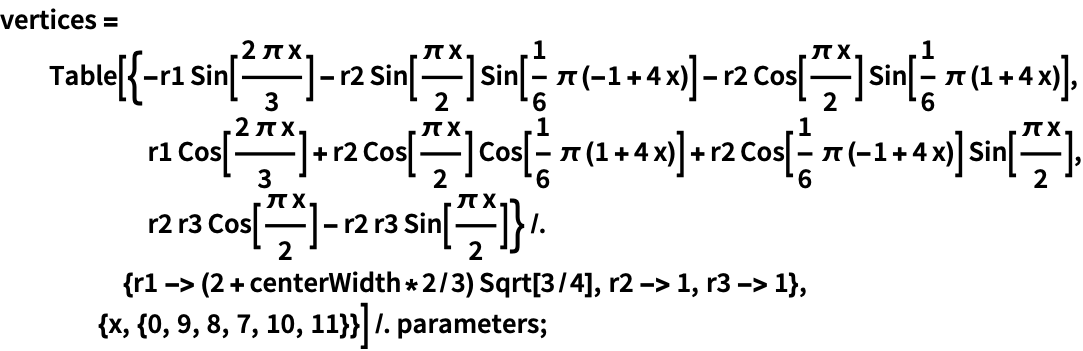
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-0uqsgw
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-uceenq
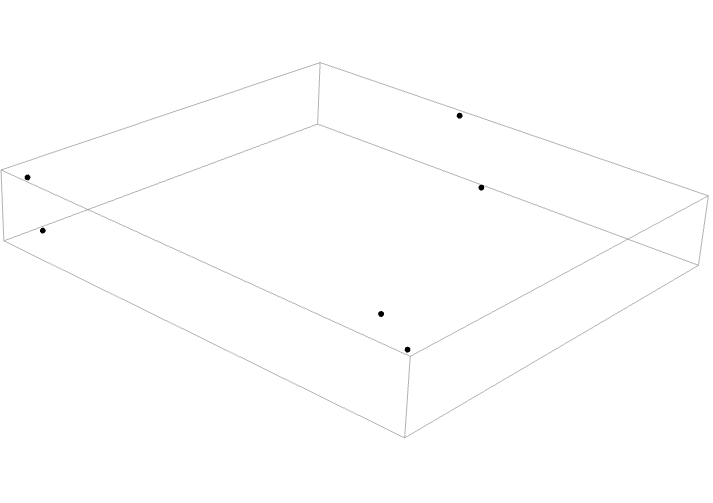
指定の位置において,頂点間の最大間隔を2乗したものを返す関数を作成する:
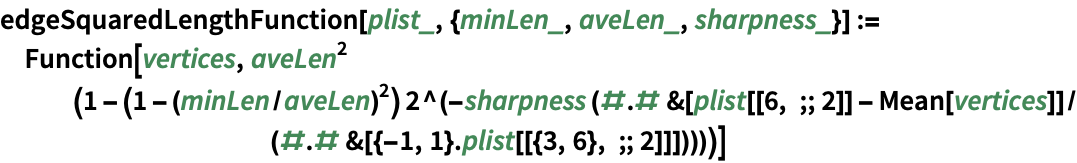
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-j1hwj1
指定の位置において,頂点間の最大間隔を2乗したものを返す関数を作成する:
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-jdfgmt
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-6zir0r
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-o3le8g
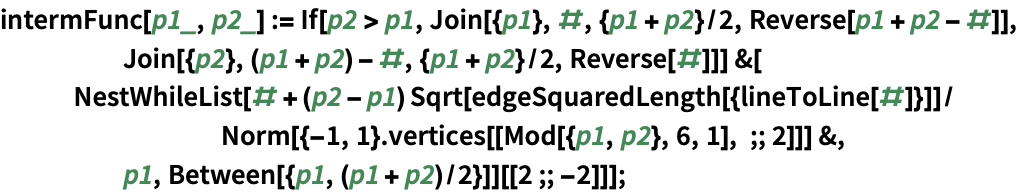
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-4cdzvd
ラプラス方程式の境界多角形を構築する.頂点は,面を接合したときに辺上のすべての頂点が適切に重なるような間隔に置かれる:

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-ldtqg2
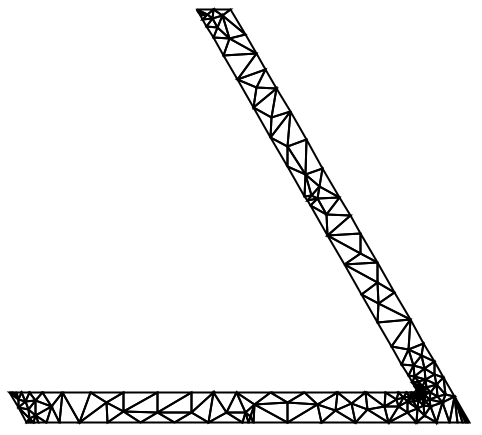
境界に点を追加せずに,ラプラス偏微分方程式を解くメッシュを作成する:

https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-k8xdup
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-mqt072
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-mn8njn
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-uiu3la
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-z9u10s
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-2cd1nl
https://wolfram.com/xid/0cy39q6twgp82cng00zxgie-pj40lp
Wolfram Research (2014), ToElementMesh, Wolfram言語関数, https://reference.wolfram.com/language/FEMDocumentation/ref/ToElementMesh.html (2022年に更新).テキスト
Wolfram Research (2014), ToElementMesh, Wolfram言語関数, https://reference.wolfram.com/language/FEMDocumentation/ref/ToElementMesh.html (2022年に更新).
Wolfram Research (2014), ToElementMesh, Wolfram言語関数, https://reference.wolfram.com/language/FEMDocumentation/ref/ToElementMesh.html (2022年に更新).CMS
Wolfram Language. 2014. "ToElementMesh." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/FEMDocumentation/ref/ToElementMesh.html.
Wolfram Language. 2014. "ToElementMesh." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/FEMDocumentation/ref/ToElementMesh.html.APA
Wolfram Language. (2014). ToElementMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FEMDocumentation/ref/ToElementMesh.html
Wolfram Language. (2014). ToElementMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FEMDocumentation/ref/ToElementMesh.htmlBibTeX
@misc{reference.wolfram_2025_toelementmesh, author="Wolfram Research", title="{ToElementMesh}", year="2022", howpublished="\url{https://reference.wolfram.com/language/FEMDocumentation/ref/ToElementMesh.html}", note=[Accessed: 05-April-2025
]}BibLaTeX
@online{reference.wolfram_2025_toelementmesh, organization={Wolfram Research}, title={ToElementMesh}, year={2022}, url={https://reference.wolfram.com/language/FEMDocumentation/ref/ToElementMesh.html}, note=[Accessed: 05-April-2025
]}