ContourPlot
ContourPlot[f,{x,xmin,xmax},{y,ymin,ymax}]
f を x と y の関数とした等高線プロットを作成する.
ContourPlot[f==g,{x,xmin,xmax},{y,ymin,ymax}]
f=g である等高線をプロットする.
ContourPlot[{f1==g1,f2==g2,…},{x,xmin,xmax},{y,ymin,ymax}]
複数の等高線をプロットする.
ContourPlot[…,{x,y}∈reg]
変数{x,y}が,幾何学領域 reg にあるものと解釈する.
詳細とオプション



- ContourPlotは,等値線,iso曲線,等位集合,あるいは下位集合しても知られている.
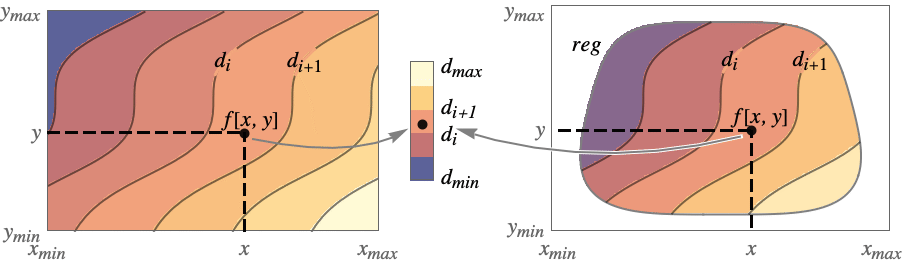
- ContourPlotは,関数 f が与えられると,f[x,y]が定数値 d1,d2等を持つ等位集合に対応する等高線を構築する.デフォルトで,値が diと di+1の間にある領域がより簡単に識別できるように曲線間の領域には陰影が付けられる.
- これは,領域
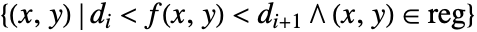 を可視化する.
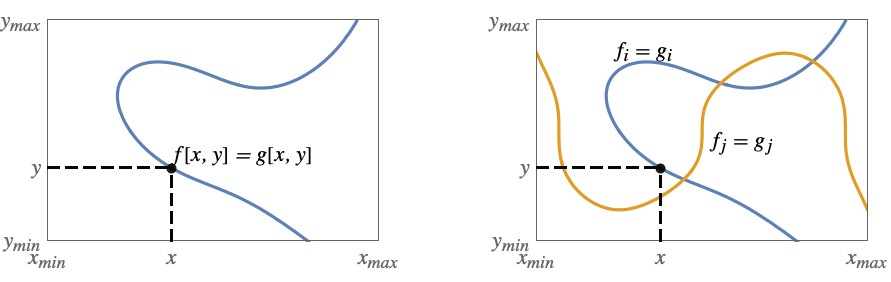
を可視化する. - ContourPlotは,等式 f==g が与えられるとこの等式を満足する{x,y}の曲線を表示する.領域の陰影付けは行われない.複数の等式からの曲線は陰影付けが無意味である任意の方法で交差することがある.これは,集合
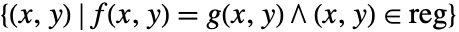 を可視化する.
を可視化する. - f が実数に評価されない位置では,等高線プロットの背景が見えるように表面に穴が残る.
- ContourPlotは,実質的にBlockを使い変数 x と変数 y を局所的なものとして扱う.
- ContourPlotには属性HoldAllがあり,x と y に特定の数値を割り当てた後ではじめて fiと giを評価する.
- 場合によっては,x と y に特定の数値が割り当てられる前にEvaluateを使って fiと giを記号的に評価した方がより効率的である.
- f を評価するとNoneになる領域のプロット部分は空白のまま残される.
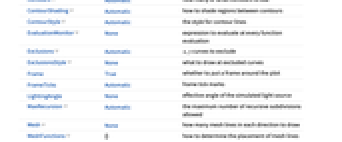
- ContourPlotには,Graphicsと同じオプションに以下が追加・修正されたものが使われる. [全オプションのリスト]
- PlotLegendsでよく使われ設定
-
None 凡例は使わない Automatic 凡例を自動的に決定する Placed[lspec,…] 凡例の置き方を指定する - ContourShading->Automaticのデフォルト設定では,ContourPlot[f,…]については陰影付けが行われるが,ContourPlot[f==g,…]については行われない.
- ContourPlot[{f1==g1,f2==g2,…},…]は,等式 fi==gi のすべてに関連する等高線を重ね合せる.
- 等高線レベル間の領域の彩色方法の決定の際,ContourPlotは,まずContourShadingに与えられた明示的な設定を調べて,その後ColorFunctionに与えられた設定を調べる.
- ContourPlotは最初に,PlotPointsで指定された等間隔に置かれたサンプル点の格子で,f を評価する.次に,適応的なアルゴリズムを用いて最高MaxRecursion回まで部分分割し,滑らかな等高線を生成する.
- ContourPlotは有限個のサンプル点しか使わないことで,関数の特徴を見付けられない可能性もあるので注意されたい.結果の検証にはPlotPointsとMaxRecursionの設定値を大きくしてみるとよい.
- PerformanceGoalの設定値によっては,他の特定のオプション設定が無効となることもある.
- MeshFunctionsとRegionFunctionの関数に渡される引数は x,y,f である.
- ColorFunctionには引数が1つ渡される.この引数はデフォルトで,連続する等高線レベルの各ペアについての f のスケールされた値の平均で渡される.
- デフォルト設定のExclusions->AutomaticおよびExclusionsStyle->Noneでは,不連続性を感知した位置で,ContourPlotのサンプリングの連続性が途絶える.この不連続性は,特定の等高レベルから飛び抜けるような場合にのみ即座に分かるようになる.
- ScalingFunctionsの可能な設定値
-
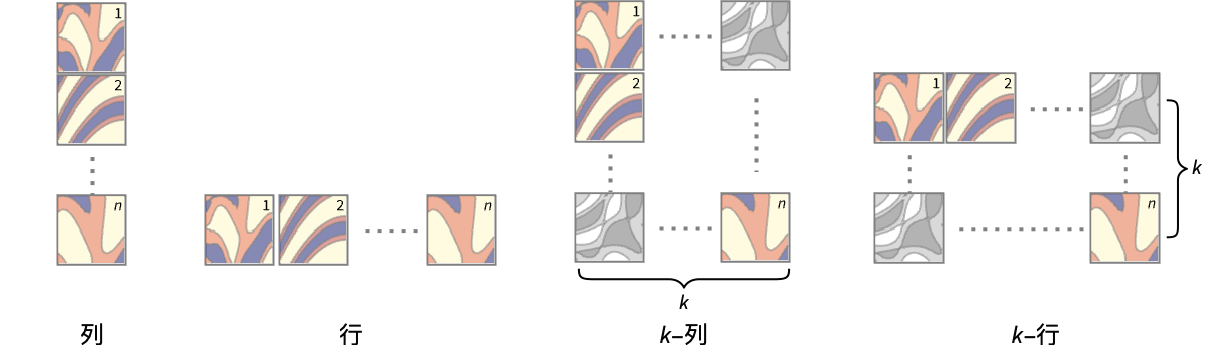
sf f の値をスケールする {sx,sy} x 軸と y 軸をスケールする {sx,sy,sf} x 軸,y 軸,f の値をスケールする - 次は,各入力を別々のプロットパネルで表示するPlotLayoutの可能な設定である.
-
"Column" パネルの列内で別々の等高線を使う "Row" パネルの行内で別々の等高線を使う {"Column",k},{"Row",k} k 列(行)を使う {"Column",UpTo[k]},{"Row",UpTo[k]} 最高で k 列(行)を使う - LightingAngle->None以外の設定では,ContourPlotはBoxRatiosが決定する高さの値に基づいた擬似照明を含む.
- ContourPlotはGraphics[GraphicsComplex[data]]を返す.
全オプションのリスト



例題
すべて開くすべて閉じるスコープ (22)
サンプリング (11)
関数が急速に変化するところではより多くの点がサンプルとして取られる:
PlotPointsとMaxRecursionを使って適応的サンプリングを制御する:
PlotRangeを使って関心領域に焦点を当てる:
Exclusionsを使って曲線を除去したり結果の曲面を分断したりする:
RegionFunctionを使って曲面を不等式によって与えられた領域に限る:
領域はMeshRegionで指定することができる:
オプション (110)
AspectRatio (4)
デフォルトで,ContourPlotは縦と横に同じ長さを使う:
AspectRatioAutomaticはプロット範囲から縦横比を決める:
AspectRatioFullは他の構造物の中にぴったり収まるように縦横比を調節する:
Axes (4)
AxesLabel (4)
BoundaryStyle (5)
BoundaryStyleはRegionFunctionによって切り取られた穴に適用される:
BoundaryStyleはExclusionsによって切り取られた部分には適用されない:
代りにExclusionsStyleを使う:
ClippingStyle (4)
ContourLines (1)
ContourLinesはContourStyleに置き換えられた:
Contours (7)
ContourShading (4)
ContourStyle (7)
Noneを使って等高線を示さないようにする:
EvaluationMonitor (2)
Exclusions (6)
ImageSize (7)
PlotLegends (8)
PlotLegendsは自動的に色関数をマッチする:
PlotLegends->Automaticとすると陰関数曲線にプレースホルダの値でラベルが付けられる:
PlotLegends->"Expressions"として実際の方程式を使う:
Placedを使って凡例の位置を変える:
BarLegendを使って凡例の外観を変える:
ScalingFunctions (9)
アプリケーション (6)
特性と関係 (6)
ContourPlotは,必要な場合はより多くの点をサンプルとして取る:
データのプロットにListContourPlotを使う:
曲面と密度にPlot3DとDensityPlotを使う:
一変量関数にPlotを使う:
ParametricPlotを平面のパラメトリック曲線と領域に使う:
陰関数の曲面と領域にContourPlot3DとRegionPlot3Dを使う:
テキスト
Wolfram Research (1988), ContourPlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/ContourPlot.html (2021年に更新).
CMS
Wolfram Language. 1988. "ContourPlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/ContourPlot.html.
APA
Wolfram Language. (1988). ContourPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ContourPlot.html