GraphPlot3D
GraphPlot3D[g]
グラフ g の3Dプロットを生成する.
GraphPlot3D[{e1,e2,…}]
辺 eiを持つグラフの3Dプロットを生成する.
GraphPlot3D[{…,w[ei],…}]
記号ラッパー w で定義された特徴を持つ eiをプロットする.
GraphPlot3D[{vi 1vj 1,…}]
規則 vikvjkを使ってグラフ g を指定する.
GraphPlot3D[m]
隣接行列 m を使ってグラフ g を指定する.
詳細とオプション



- GraphPlot3Dは,うまく配置されたグラフを与えるように,頂点を3Dに位置付けようとする.
- GraphPlot3Dは,Graphと同じ,頂点,辺,ラッパーをサポートする.
- 辺 eiには,次の特殊ラッパーが使える.
-
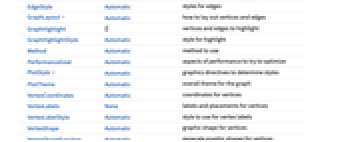
Annotation[ei,label] 注釈を与える Button[ei,action] 要素がクリックされたときに実行する動作を定義する EventHandler[ei,…] 要素の一般的なイベントハンドラを定義する Hyperlink[ei,uri] 要素をハイパーリンクにする Labeled[ei,…] 要素にラベルを付けて表示する PopupWindow[ei,cont] 要素にポップアップウィンドウを付ける StatusArea[ei,label] 要素がマウスオーバーされたときにステータスエリアに表示する Style[ei,opts] 要素を指定のスタイルで表示する Tooltip[ei,label] 要素に任意のツールチップを付ける - GraphPlot3Dでは,Graphics3Dと同じオプションに次の追加・修正を加えたものが使える. [全オプションのリスト]
-
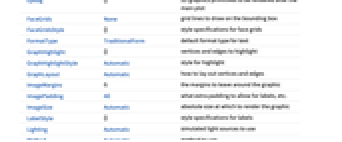
DataRange Automatic 生成する頂点の座標の範囲 DirectedEdges False RuleをDirectedEdgeと解釈するかどうか EdgeLabels None 辺のラベルと置き方 EdgeLabelStyle Automatic 辺のラベルのスタイル EdgeShapeFunction Automatic 辺の図形を生成する EdgeStyle Automatic 辺のスタイル GraphLayout Automatic 頂点と辺をどのように並べるか GraphHighlight {} ハイライトする辺と頂点 GraphHighlightStyle Automatic ハイライトのスタイル Method Automatic 使用するメソッド PerformanceGoal Automatic パフォーマンスのどの面について最適化するか PlotStyle Automatic スタイルを決定するグラフィックス指示子 PlotTheme Automatic グラフの全体的なテーマ VertexCoordinates Automatic 頂点座標 VertexLabels None 頂点のラベルと置き方 VertexLabelStyle Automatic 頂点ラベルに使うスタイル VertexShape Automatic 頂点の形 VertexShapeFunction Automatic 頂点の形を生成する VertexSize Automatic 頂点の大きさ VertexStyle Automatic 頂点のスタイル - VertexCoordinates->Automaticの設定のとき,頂点の埋込みと辺の経路の決定は,GraphLayoutの設定に基づいて自動的に計算される.
- GraphLayoutの特別な埋込みには以下がある.
-
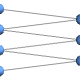
"BipartiteEmbedding" 2本の平行線上の頂点 
"CircularEmbedding" 円周上の頂点 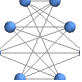
"CircularMultipartiteEmbedding" 弓形の上の頂点 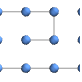
"DiscreteSpiralEmbedding" 離散螺線上の頂点 
"GridEmbedding" 格子上の頂点 
"LinearEmbedding" 直線上の頂点 
"MultipartiteEmbedding" 複数の平行線上の頂点 
"SpiralEmbedding" 2Dに投影された3D螺旋上の頂点 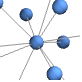
"StarEmbedding" 中心がある円上の頂点 - 木グラフや有向非巡回グラフのような階層的グラフの構造化埋込みには以下がある.
-
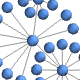
"BalloonEmbedding" 中心が親頂点にある円の上の頂点 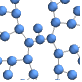
"RadialEmbedding" 弓形の上の頂点 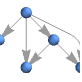
"LayeredDigraphEmbedding" 有向非巡回グラフの平行線上の頂点 
"LayeredEmbedding" 平行線上の頂点 - 最適化埋込みはすべて数量を最小化する.以下はその可能なものである.
-
"HighDimensionalEmbedding" 高次元のバネ電気のエネルギー 
"PlanarEmbedding" 辺交差の数 
"SpectralEmbedding" 平方距離の重み付き和 
"SpringElectricalEmbedding" ババネとしての辺と電荷としての頂点を持つエネルギー 
"SpringEmbedding" 辺をバネとして持つエネルギー 
"TutteEmbedding" 辺交差の数と近傍の距離 - PlotThemeの可能な設定には,一般的な基本テーマ,色の特徴テーマ,フォントの特徴テーマ,サイズの特徴テーマがある.
-
"Business" 明るい近代的な外観.ビジネスプレゼンテーションやインフォグラフィックスに適している 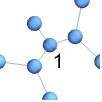
"Detailed" ラベルやツールチップを使ってデータを識別する 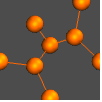
"Marketing" マーケティングに適した,エレガントで目を引くデザイン 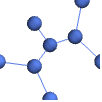
"Minimal" 単純なグラフ 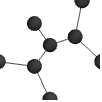
"Monochrome" 単色のデザイン 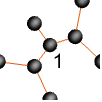
"Scientific" ラベルやツールチップが付いた,詳細データの分析に役立つ自然のままのデザイン 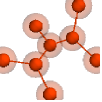
"Web" 消費者向けのWebサイトやブログに適したクリーンで大胆なデザイン 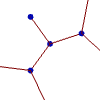
"Classic" 既存の用途との互換性を維持するための,プロットの従来のデザイン - グラフの特徴テーマは頂点と辺のプロットに影響する.特徴テーマには以下がある.
-
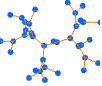
"LargeGraph" 大きいグラフ 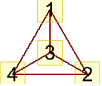
"ClassicLabeled" 従来のグラフ 
"IndexLabeled" 指標ラベルが付いたグラフ
全オプションのリスト

例題
すべて開くすべて閉じるスコープ (12)
グラフの指定 (6)
GraphDataを一群のグラフに使う:
ExampleDataを一群の疎行列に使う:
グラフのスタイル付け (6)
非常に大きいグラフの場合,頂点は全く描かない方がよいことが多い:
EdgeShapeFunctionとVertexShapeFunctionを使って詳細を制御する:
オプション (71)
GraphLayout (66)
"BalloonEmbedding" (6)
"CircularMultipartiteEmbedding" (2)
"DiscreteSpiralEmbedding" (3)
"DiscreteSpiralEmbedding"は経路グラフに最も適している:
"OptimalOrder"Trueの設定のとき,離散螺線上にきれいに置かれるように頂点が並べ替えられる:
"HighDimensionalEmbedding" (2)
"LayeredEmbedding" (6)
"LayeredDigraphEmbedding" (3)
"SpectralEmbedding" (2)
"SpiralEmbedding" (2)
"SpringElectricalEmbedding" (12)
各頂点が電荷を持ち,各辺がバネに対応する場合に,力学的エネルギーおよび電気エネルギーが最小になるように頂点を置く:
"EdgeWeighted"->Trueの設定のときは,辺の重みが使われる:
"EnergyControl"->e を使って最小化の最中の系の総エネルギーに対する制限を指定する:
"InferentialDistance"->d を使って,そこを超えると頂点間のインタラクションが存在しないと仮定されるカットオフ距離を指定する:
"MaxIteration"->it を使ってエネルギーを最小にするために使われる反復の最大数を指定する:
"Multilevel"->method を使ってグラフを粗くする再帰的手順に使用するメソッドを指定する:
"Octree"->Trueの設定のときは,反発力の計算に(三次元の)八分木のデータ構造あるいは(二次元の)四分木データ構造が使われる:
"RandomSeed"->int を使って初期の頂点位置を計算する乱数生成器のシードを指定する:
"RepulsiveForcePower"->r を使って,反発力の距離による減衰の速度を制御する:
"StepControl"->method を使って,エネルギーの最小化の最中にどのようにステップ長を変更するか定義する:
"SpringEmbedding" (10)
各辺がバネに相当するときに力学的エネルギーを最小化するように頂点を置く:
"EdgeWeighted"->Trueと設定すると,辺の重みが使われる:
オプション"EnergyControl"->e を使って最小化中の系の総エネルギーに対する制限を指定する:
"InferentialDistance"->d を使って,それを超えては頂点間の相互作用が存在しないと仮定されるカットオフ距離を指定する:
"MaxIteration"->it を使って,エネルギーを最小化しようとする過程で使用する最大反復回数を指定する:
"Multilevel"->method を使って,グラフを粗くする再帰的手順で使われるメソッドを指定する:
"RandomSeed"->int を使って,初期頂点位置を計算する乱数生成器のシードを指定する:
"StepControl"->method を使って,エネルギーの最小化の過程でどのようにステップ長を修正するかを定義する:
"StarEmbedding" (3)
PlotStyle (3)
PlotStyleはより優先順位が高いVertexShapeFunctionとともに使うことができる:
PlotStyleはより優先順位が高いEdgeShapeFunctionとともに使うことができる:
特性と関係 (7)
LayeredGraphPlotを有向グラフの階層スタイルの描画に使う:
TreePlotを異なるタイプのツリー描画に使う:
GraphPlotを使って2Dのグラフを描画する:
GraphDataを予め指定されたグラフと特性の大規模な集合に使う:
PolyhedronDataを多面体と特性の大規模集合に使う:
ExampleDataを疎行列の大規模集合に使う:
ArrayPlotあるいはMatrixPlotを使って疎行列を表示する:
テキスト
Wolfram Research (2007), GraphPlot3D, Wolfram言語関数, https://reference.wolfram.com/language/ref/GraphPlot3D.html (2019年に更新).
CMS
Wolfram Language. 2007. "GraphPlot3D." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/GraphPlot3D.html.
APA
Wolfram Language. (2007). GraphPlot3D. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphPlot3D.html