LineIntegralConvolutionPlot[{{vx,vy},image},{x,xmin,xmax},{y,ymin,ymax}]
产生一个线积分卷积图形,image 和关于 x、y 的矢量场 {vx,vy} 的卷积.
LineIntegralConvolutionPlot[{vx,vy},{x,xmin,xmax},{y,ymin,ymax}]
产生白噪音和矢量场 {vx,vy} 的一个线积分卷积图形.




LineIntegralConvolutionPlot
LineIntegralConvolutionPlot[{{vx,vy},image},{x,xmin,xmax},{y,ymin,ymax}]
产生一个线积分卷积图形,image 和关于 x、y 的矢量场 {vx,vy} 的卷积.
LineIntegralConvolutionPlot[{vx,vy},{x,xmin,xmax},{y,ymin,ymax}]
产生白噪音和矢量场 {vx,vy} 的一个线积分卷积图形.
更多信息和选项

- LineIntegralConvolutionPlot 创建一个栅格化 image,然后根据矢量函数 {vx,vy} 定义的域对每个像素进行线积分卷积.
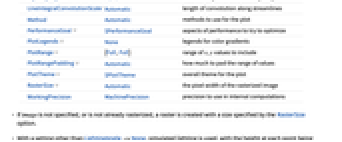
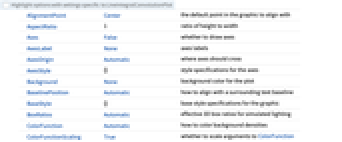
- LineIntegralConvolutionPlot 与 Graphics 的选项相同,并附加下列选项和变化: [所有选项的列表]
-
AspectRatio 1 高宽比 BoxRatios Automatic 模拟光照的三维框的比率 ColorFunction Automatic 如何着色背景密度 ColorFunctionScaling True 是否缩放传递给 ColorFunction 的参数 EvaluationMonitor None 每次函数运算时,计算的表达式 Frame True 是否在图形周围绘制一个边框 FrameTicks Automatic 边框刻度标记 LightingAngle None 模拟光源的实际角度 LineIntegralConvolutionScale Automatic 沿着流线的卷积的长度 Method Automatic 用于绘制的方法 PerformanceGoal $PerformanceGoal 优化执行的性能方面 PlotLegends None 颜色梯度的图例 PlotRange {Full,Full} 包含 x,y 值的范围 PlotRangePadding Automatic 如何填充值的范围 PlotTheme $PlotTheme 图线的整体主题 RasterSize Automatic 栅格化图像的像素宽度 WorkingPrecision MachinePrecision 内部计算的精度 - 如果没有指定 image,或没有栅格化,则创建一个光栅,光栅的大小由选项 RasterSize 确定.
- 除了 LightingAngle->None 的设置外,使用模拟光照,每个点的高度根据矢量场的范数确定.
- ColorFunction 的参数是 x、y、vx、vy、Norm[{vx,vy}].
所有选项的列表


范例
打开所有单元 关闭所有单元范围 (12)
选项 (72)
AspectRatio (4)
默认情况下,LineIntegralConvolutionPlot 使用相同的宽和高:
AspectRatioAutomatic 根据绘图范围确定高宽比:
AspectRatioFull 调整高度和宽度以紧密适合其他结构:
Axes (3)
ColorFunction (5)
使用 Hue 对场量进行着色:
使用 ColorData 中的任意已命名颜色梯度:
使用 ColorData 的预定义颜色梯度:
使用 ColorFunctionScaling->False 得到尺度未调整的值:
ColorFunctionScaling (4)
使用 ColorFunctionScaling->False 得到尺度未调整的值:
FrameTicks (8)
使用 FrameTicksStyle 指定包括刻度标签在内的整体边框刻度风格:
ImageSize (7)
PlotLegends (2)
PlotRange (7)
PlotRangePadding (6)
应用 (5)
应用一种来自 ExampleData 的纹理:
属性和关系 (4)
用 ListLineIntegralConvolutionPlot 对数据绘图:
使用 VectorPlot3D 和 StreamPlot3D 可视化三维向量场:
相关指南
-
▪
- 向量可视化
文本
Wolfram Research (2008),LineIntegralConvolutionPlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/LineIntegralConvolutionPlot.html (更新于 2014 年).
CMS
Wolfram 语言. 2008. "LineIntegralConvolutionPlot." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/LineIntegralConvolutionPlot.html.
APA
Wolfram 语言. (2008). LineIntegralConvolutionPlot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/LineIntegralConvolutionPlot.html 年
BibTeX
@misc{reference.wolfram_2025_lineintegralconvolutionplot, author="Wolfram Research", title="{LineIntegralConvolutionPlot}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/LineIntegralConvolutionPlot.html}", note=[Accessed: 10-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_lineintegralconvolutionplot, organization={Wolfram Research}, title={LineIntegralConvolutionPlot}, year={2014}, url={https://reference.wolfram.com/language/ref/LineIntegralConvolutionPlot.html}, note=[Accessed: 10-February-2026]}