ListLineIntegralConvolutionPlot
ListLineIntegralConvolutionPlot[{array,image}]
ベクトル場の値の配列で定義されたベクトル場でたたみ込まれた image の線形積分たたみ込みプロットを生成する.
ListLineIntegralConvolutionPlot[array]
array で定義されたベクトル場でたたみ込まれたホワイトノイズの線形積分たたみ込みプロットを生成する.
ListLineIntegralConvolutionPlot[{{{{x1,y1},{vx1,vy1}},…},image}]
指定の点{xi,yi}でベクトル{vxi,vyi}で定義されたベクトル場でたたみ込まれた image の線形積分たたみ込みプロットを生成する.
ListLineIntegralConvolutionPlot[{{{x1,y1},{vx1,vy1}},…}]
{vxi,vyi}で定義されたベクトル場でたたみ込まれたホワイトノイズの線形積分たたみ込みプロットを生成する.
詳細とオプション


- LineIntegralConvolutionPlotは image のラスタライズしたものを作成し,次に与えられたベクトルデータを補間して定義された場に従って個々の画素の線形積分たたみ込みを行う.
- ListLineIntegralConvolutionPlotにはGraphicsのオプションと同じものに次の追加・変更を加えたものが使える. [全オプションのリスト]
-
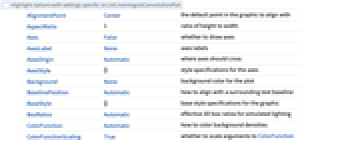
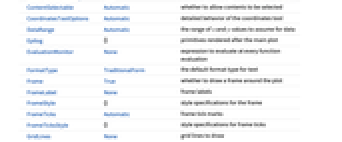
AspectRatio 1 縦横比 BoxRatios Automatic 擬似照明の事実上の3Dボックス比 ColorFunction Automatic 背景濃度をどのように彩色するか ColorFunctionScaling True ColorFunctionの引数をスケールするかどうか DataRange Automatic データとして仮定する x 値と y 値の範囲 EvaluationMonitor None 各関数の評価で評価する式 LineIntegralConvolutionScale Automatic 流線に沿ったたたみ込みの長さ Frame True プロット周囲に枠を描くかどうか FrameTicks Automatic 枠目盛マーク LightingAngle None 擬似照明の事実上の角度 Method Automatic プロットに使用するメソッド PerformanceGoal $PerformanceGoal パフォーマンスのどの面について最適化するか PlotLegends None プロットの凡例 PlotRange {Full,Full} 含める x, y 値の範囲 PlotRangePadding Automatic 値の範囲をどの程度充填するか PlotTheme $PlotTheme プロットの全体的なテーマ RasterSize Automatic ラスタライズされた画像のピクセル幅 WorkingPrecision MachinePrecision 内部計算で使用する精度 - image が指定されていなければ,あるいはまだラスタライズされていなければ,RasterSizeオプションで指定されたサイズでラスタが作成される.
- LightingAngle->None以外の設定では,各点における高さがベクトル場の法線によって決定されると考えられる擬似照明が使用される.
- ColorFunctionに渡される引数は x, y, vx, vy, Norm[{vx,vy}]である.
全オプションのリスト

例題
すべて開くすべて閉じるスコープ (10)
オプション (44)
ColorFunction (5)
Hueを使って場の強度に彩色する:
ColorDataから任意の名前付き色階調度を使う:
定義済みの色階調度にColorDataを使う:
ColorFunctionScaling->Falseを使ってスケールされていない値を得る:
ColorFunctionScaling (4)
ColorFunctionScaling->Falseを使ってスケールされていない値を得る:
FrameTicks (8)
枠目盛ラベルを含む全体的な枠目盛のスタイルをFrameTicksStyleを使って指定する:
PlotLegends (1)
PlotRange (7)
PlotRangePadding (6)
特性と関係 (4)
LineIntegralConvolutionPlotを使って関数をプロットする:
ListVectorPlot3DとListStreamPlot3D を使って3Dのベクトル場データを可視化する:
テキスト
Wolfram Research (2008), ListLineIntegralConvolutionPlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/ListLineIntegralConvolutionPlot.html (2014年に更新).
CMS
Wolfram Language. 2008. "ListLineIntegralConvolutionPlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/ListLineIntegralConvolutionPlot.html.
APA
Wolfram Language. (2008). ListLineIntegralConvolutionPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ListLineIntegralConvolutionPlot.html