NearestNeighborGraph
NearestNeighborGraph[{elem1,elem2,…}]
頂点を elem1,elem2,…とし,各 elemiをその最近傍と繋ぐ辺を持つグラフを与える.
NearestNeighborGraph[{elem1,elem2,…},k]
各 elemiをその k 最近傍と繋ぐグラフを与える.
NearestNeighborGraph[{elem1,elem2,…},{k,r}]
各 elemiを elemiの半径 r 以内の最高で k 個の最近頂点 と繋ぐグラフを与える.
NearestNeighborGraph[{elem1,elem2,…},{All,r}]
各 elemiと elemiの半径 r 以内のすべての頂点を繋ぐグラフを与える.
詳細とオプション

- 最近傍グラフは,k 最近傍グラフ(k-NNG)としても知られている.
- elemiから elemjまでの距離が elemiから任意の他の要素までの距離より大きくない場合は常に,要素 elemjは要素 elemiの最近傍である.
- elemiから elemjまでの距離が elemiから他の任意の要素までの k 番目までの最短距離に含まれる場合は常に,要素 elemjは要素 elemiの k 最近傍である.
- NearestNeighborGraphは,数値,地理空間,テキスト,ビジュアルを含むさまざまなデータに使うことができる.
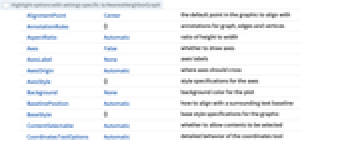
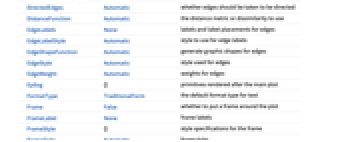
- NearestNeighborGraphには,Graphと同じオプションに次の追加・変更を加えたものを使うことができる. [全オプションのリスト]
-
DirectedEdges Automatic 辺を有向とみなすかどうか DistanceFunction Automatic 使用する距離測度あるいは非類似度 WorkingPrecision Automatic 数値データに使用する精度 - NearestNeighborGraphはNearestと同じDistanceFunctionを取る.
全オプションのリスト


例題
すべて開くすべて閉じるスコープ (10)
オプション (89)
DistanceFunction (7)
デフォルトで,数値データにはEuclideanDistanceが使われる:
EditDistanceは文字列に使われる:
GeoDistanceは地理位置に使われる:
JaccardDissimilarityはブールデータに使われる:
ColorDistanceは色に使われる:
ImageDistanceは画像に使われる:
DistanceFunctionは記号として与えることができる:
WorkingPrecision (1)
WorkingPrecision->MachinePrecisionを使うと最も速い評価メソッドが使われる:
DirectedEdges (1)
DirectedEdges->Trueを使って有向グラフを生成する:
EdgeLabels (7)
Placedを記号的な位置と一緒に使って辺に沿ったラベルの置き方を制御する:
TooltipとStatusAreaからの値によって自動ラベル付けを行う:
EdgeShapeFunction (6)
EdgeShapeFunctionについての組込み設定のリストを得る:
EdgeShapeFunctionはEdgeStyleと組み合せることができる:
EdgeShapeFunctionはEdgeStyleより優先順位が高い:
GraphHighlightStyle (2)
GraphLayout (5)
VertexCoordinatesはGraphLayout座標を上書きする:
AbsoluteOptionsによってレイアウトアルゴリズムを使って計算されたVertexCoordinatesを抽出する:
VertexCoordinates (3)
AbsoluteOptionsを使って結果の頂点座標を抽出する:
VertexCoordinatesはGraphLayoutより優先順位が高い:
VertexLabels (13)
Placedを記号的な位置と一緒に使って,外側位置を含むラベルの置き方を制御する:
すべてのラベルを頂点の右上コーナーに置き,ラベル内の座標を変える:
引数Placedを使ってTooltipを含むフォーマットを制御する:
あるいはStatusAreaを含む:
VertexShape (5)
任意のGraphics,ImageあるいはGraphics3Dを頂点の形として使う:
VertexShapeはVertexSizeと組み合せることができる:
VertexShapeはVertexStyleの影響を受けない:
VertexShapeFunctionはVertexShapeより優先順位が高い:
VertexShapeFunction (10)
VertexShapeFunctionの組込みコレクションのリストを得る:
"Basic"コレクション中のVertexShapeFunctionの組込み設定を使う:
"Rounded"コレクション中のVertexShapeFunctionの組込み設定を使う:
"Concave"コレクション中のVertexShapeFunctionの組込み設定を使う:
VertexShapeFunctionはVertexStyleと組み合せることができる:
VertexShapeFunctionはVertexStyleより優先順位が高い:
VertexShapeFunctionはVertexSizeより優先順位が高い:
VertexShapeFunctionはVertexShapeより優先順位が高い:
VertexSize (8)
VertexSizeはVertexShapeFunctionと組み合せることができる:
VertexSizeはVertexShapeと組み合せることができる:
VertexStyle (5)
VertexShapeFunctionはVertexStyleと組み合せることができる:
VertexShapeFunctionはVertexStyleより優先順位が高い:
VertexStyleはBaseStyleと組み合せることができる:
VertexStyleはBaseStyleより優先順位が高い:
VertexShapeはVertexStyleの影響は受けない:
アプリケーション (7)
特性と関係 (7)
VertexCountとEdgeCountを使って頂点と辺を数える:
VertexListとEdgeListを使って頂点と辺が標準的な並び順になるようにする:
グラフからAdjacencyMatrixを計算する:
SpatialGraphDistributionを使って半径0.2以内の最近傍グラフを生成する:
NearestとNearestFunctionを使って最近傍グラフを得る:
テキスト
Wolfram Research (2015), NearestNeighborGraph, Wolfram言語関数, https://reference.wolfram.com/language/ref/NearestNeighborGraph.html.
CMS
Wolfram Language. 2015. "NearestNeighborGraph." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NearestNeighborGraph.html.
APA
Wolfram Language. (2015). NearestNeighborGraph. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NearestNeighborGraph.html