NormalDistribution
NormalDistribution[μ,σ]
平均 μ,標準偏差 σ の正規(ガウス)分布を表す.
平均がゼロで標準偏差が1である正規分布を表す.
詳細
- 正規分布における値
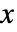 の確率密度は
の確率密度は 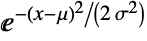 に比例する. »
に比例する. » - NormalDistributionでは μ は任意の実数,σ は任意の正の実数でよい.
- NormalDistributionでは,μ と σ は単位次元が等しい任意の数量でよい. »
- NormalDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- NormalDistribution[μ,σ]は,実領域上で定義される,いわゆる「正規」統計分布を表す.この分布は,実数 μ および正の実数 σ でパラメータ化される.ただし,μ は分布の平均,σ は標準偏差,σ2は分散として知られている.正規分布の確率密度関数(PDF)は単峰で,その峰は平均
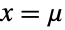 にあり,パラメータ σ はPDFの高さとその裾部の「厚さ」の両方を決定する.正規分布のPDFは,その最大値について対称であり,そのPDFの裾部はPDFが
にあり,パラメータ σ はPDFの高さとその裾部の「厚さ」の両方を決定する.正規分布のPDFは,その最大値について対称であり,そのPDFの裾部はPDFが 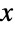 の大きい値について指数的に減少するという意味で「薄い」.(この動作は,分布のSurvivalFunctionを分析することで数量的に正確にすることができる.) 引数0の形式であるNormalDistribution[]はNormalDistribution[0,1]に等しく,標準正規分布と呼ばれることがある.
の大きい値について指数的に減少するという意味で「薄い」.(この動作は,分布のSurvivalFunctionを分析することで数量的に正確にすることができる.) 引数0の形式であるNormalDistribution[]はNormalDistribution[0,1]に等しく,標準正規分布と呼ばれることがある. - 正規分布は,そのPDFにガウス関数
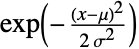 が現れることから,ガウス分布と呼ばれることがある.非公式ではあるが,正規分布はそのPDFがベルのような形になることから,「ベル曲線」と言われることもある,しかし,CauchyDistribution,StudentTDistribution,LogisticDistribution等の他の分布も数量的に「ベル」の形に似て表示される点に注意が必要である.
が現れることから,ガウス分布と呼ばれることがある.非公式ではあるが,正規分布はそのPDFがベルのような形になることから,「ベル曲線」と言われることもある,しかし,CauchyDistribution,StudentTDistribution,LogisticDistribution等の他の分布も数量的に「ベル」の形に似て表示される点に注意が必要である. - 正規分布に従う確率変数は標準変量と呼ばれることがあり,標準正規分布は単位正規分布と呼ばれることもある.
- 正規分布は,最も広く見られる確率分布の1つであり,多くの分野に応用されている.例えば,正規分布に従う値はモンテカルロ法の応用において基本的な重要性を持つ.さらに,正規分布は,独立の増分
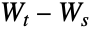 からなるいわゆるウィナー過程,連続時間確率過程
からなるいわゆるウィナー過程,連続時間確率過程 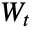 の定義においても基本的な役割を果たしている.それぞれの増分は,独立で,
の定義においても基本的な役割を果たしている.それぞれの増分は,独立で,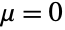 ,かつ
,かつ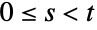 について
について 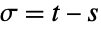 である同一正規分布に従う,また,パーセンタイル順位や
である同一正規分布に従う,また,パーセンタイル順位や 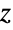 スコアおよび
スコアおよび 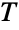 スコアを含む確率値および統計値の多くが,正規分布から導かれている.さらに,中心極限定理のために,十分な数がある独立確率変数の平均は,ある種の仮定が満たされるならば,値を表現するもとの分布には無関係に,正規分布の近似となる.正規分布は,また,理想気体分子の速度,拡散中の粒子の位置,長期間に渡る温度ランプの動作等,数多くの物理現象をモデル化する際に自然に現れる.加えて,生体組織の大きさや空腹時の血糖レベルや血圧等の数量等多くの生物学現象に見られる変数も,その対数が正規分布に従うことが多い.
スコアを含む確率値および統計値の多くが,正規分布から導かれている.さらに,中心極限定理のために,十分な数がある独立確率変数の平均は,ある種の仮定が満たされるならば,値を表現するもとの分布には無関係に,正規分布の近似となる.正規分布は,また,理想気体分子の速度,拡散中の粒子の位置,長期間に渡る温度ランプの動作等,数多くの物理現象をモデル化する際に自然に現れる.加えて,生体組織の大きさや空腹時の血糖レベルや血圧等の数量等多くの生物学現象に見られる変数も,その対数が正規分布に従うことが多い. - RandomVariateを使って,正規分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,NormalDistribution[μ,σ]](より簡略すると xNormalDistribution[μ,σ])を使って,確率変数 x が正規分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[NormalDistribution[μ,σ],x]およびCDF[NormalDistribution[μ,σ],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合が正規分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータから正規パラメトリック分布を推定することが,FindDistributionParametersを使ってデータを正規分布にフィットすることができる.ProbabilityPlotを使って記号正規分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号正規分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された正規分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って正規分布を含む高次元分布を構築することが,ProductDistributionを使って正規分布を含む独立成分分布の結合分布を計算することができる.
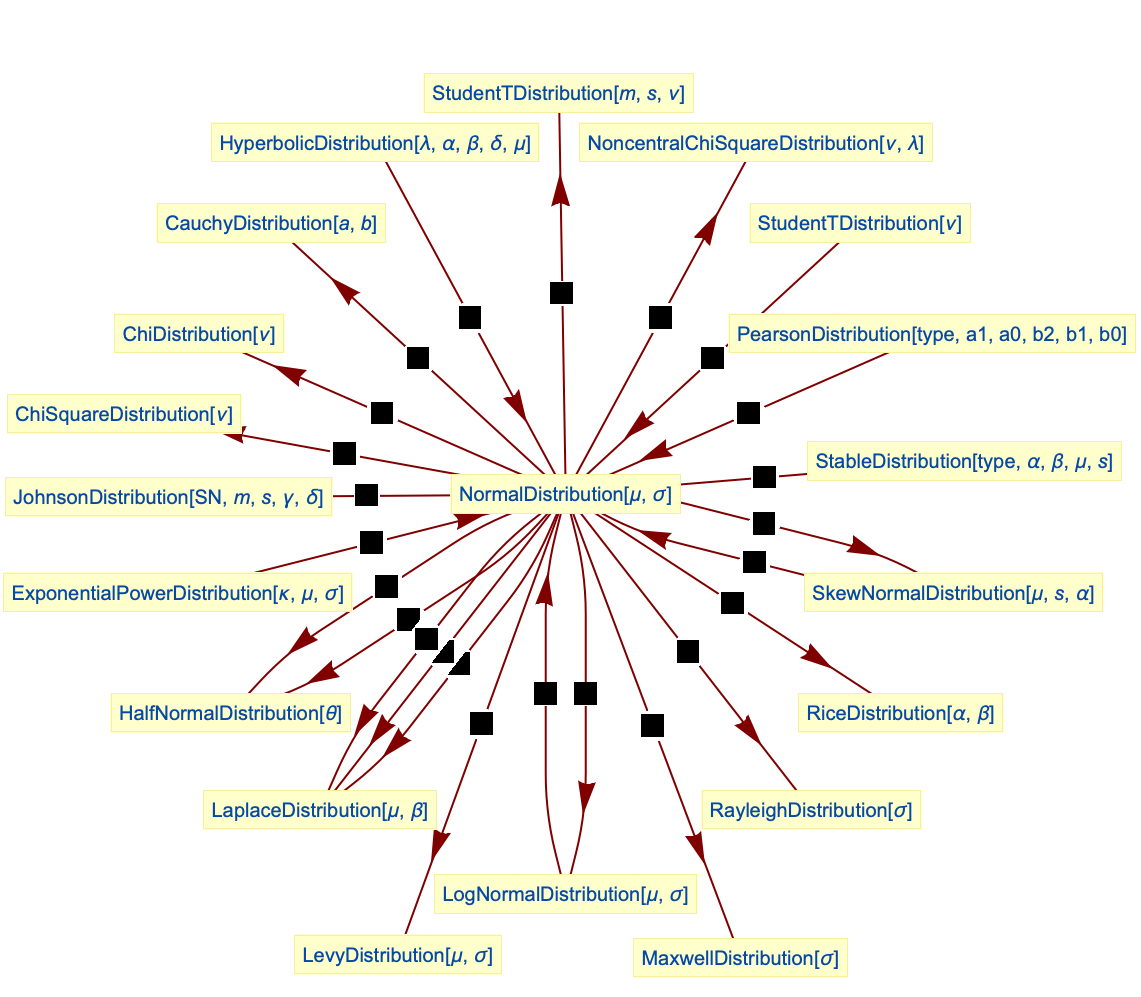
- NormalDistributionは他の多くの分布と密接に関係している.LogNormalDistribution,HalfNormalDistribution,NoncentralChiSquareDistribution,LevyDistributionを含む数多くの分布が,NormalDistributionを変換した形であると見ることができる.また,NormalDistributionはHyperbolicDistribution,StudentTDistribution,PoissonDistribution,BinomialDistributionを含む多くの関数の極限のケースであると考えることができる.加えて,NormalDistributionはExponentialPowerDistribution(PDF[NormalDistribution[μ,σ],x]はPDF[ExponentialPowerDistribution[2,μ,σ],x]に等しい),SkewNormalDistribution(PDF[NormalDistribution[μ,σ],x]はPDF[SkewNormalDistribution[μ,σ,0],x]に等しい),PearsonDistribution(PDF[NormalDistribution[μ,σ],x]はPDF[PearsonDistribution[3,σ-2,-μ σ-2,0,0,1],x]に等しい,ただし σ>0のとき)の特殊ケースであり,BinormalDistributionおよびMultinormalDistributionの周辺分布である.NormalDistributionは,StableDistribution,RiceDistribution,RayleighDistribution,MaxwellDistribution,LevyDistribution,LaplaceDistribution,JohnsonDistribution,ChiDistribution,ChiSquareDistributionと密接な関係がある.
例題
すべて開くすべて閉じるスコープ (7)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (11)
寿命が平均1000時間,標準偏差50時間でほぼ正規分布に従う電池がある.寿命が800時間から1000時間までに入る割合を求める:
100個の電池の中で寿命が800時間から1000時間までに入る個数を計算する:
一袋5ポンドで売られているコーヒー豆がある.この実際の重さは,平均5ポンド,分散0.01平方ポンド(lb![]() )の正規分布に従うとする.任意の袋の重さが少なくとも4ポンド15オンスになる確率を求める:
)の正規分布に従うとする.任意の袋の重さが少なくとも4ポンド15オンスになる確率を求める:
これは,直接SurvivalFunctionを使って求めることもできる:
ある会社が釘を製造している.この釘の長さは平均0.497インチ,標準偏差0.002インチで正規分布に従うとする.長さが0.5インチプラスマイナス0.004インチの仕様を満たす割合を求める:
CDFを使った直接計算:
ある会社が釘を製造している.この釘の長さは平均0.5インチで正規分布に従う.製造した釘の50%の長さが0.495インチより長く0.505インチより短い場合の標準偏差を求める:
平均5で標準偏差1.5の分布からサンプルを選ぶ.確率0.97でサンプルの平均が分布の平均の0.8以内になるためのサンプルの最小サイズ ![]() を求める:
を求める:
乗客の体重と手荷物の重さを合わせたものは平均225ポンド,標準偏差50ポンドの正規分布に従う.ある飛行機の積載量の上限は1万ポンドで旅客定員は44名である.満席の場合に飛行機が過積載となる確率を求める:
伝統的に,正規分布は前日終値からの株価変動率の分析に使われてきた.スタンダード&プアーズ(S&P)500種指数の2000年1月1日から2009年1月1日までの日々の株価変動率の推定分布を求める:
LogisticDistributionは正規分布よりもよいフィットを与えることを示す:
特性と関係 (36)
正規(SN)JohnsonDistributionは正規分布である:
![]() が
が ![]() に近付くにつれ,StudentTDistributionは正規分布に近付く:
に近付くにつれ,StudentTDistributionは正規分布に近付く:
正規分布はLogNormalDistributionを変換したものである:
正規分布の逆変換はLogNormalDistributionを与える:
HalfNormalDistributionは切断正規分布である:
HalfNormalDistributionは正規分布を変換したものである:
HalfNormalDistributionは正規分布を変換したものである:
NormalDistributionはExponentialPowerDistributionの特殊ケースである:
正規分布はSkewNormalDistributionの特殊ケースで形状母数が ![]() である:
である:
SkewNormalDistributionは正規分布を変換したものである:
標準正規分布に従う ![]() 個の変数の平方和はChiSquareDistributionに従う:
個の変数の平方和はChiSquareDistributionに従う:
正規分布に従う変数の平方和はNoncentralChiSquareDistributionに従う:
標準正規分布に従う ![]() 個の変数のノルムはChiDistributionに従う:
個の変数のノルムはChiDistributionに従う:
標準正規分布に従う3個の変数のノルムはChiDistributionの一つ,MaxwellDistributionに従う:
標準正規分布に従う2個の変数のノルムはRayleighDistribution分布に従う:
正規分布に従う2つの変数のノルムはRiceDistributionに従う:
NormalDistributionは,![]() と
と![]() について
について ![]() のHyperbolicDistributionの極限のケースである:
のHyperbolicDistributionの極限のケースである:
![]() ,
,![]() ,
,![]() ,
,![]() が独立で正規分布に従うなら,
が独立で正規分布に従うなら,![]() はLaplaceDistributionに従う:
はLaplaceDistributionに従う:
CharacteristicFunctionの等価性を使って確かめる:
![]() ,
,![]() ,
,![]() ,
,![]() が独立で正規分布に従うなら,
が独立で正規分布に従うなら,![]() はLaplaceDistributionに従う:
はLaplaceDistributionに従う:
CharacteristicFunctionの等価性を使って確かめる:
正規分布に従う2つの変数の比はCauchyDistributionを示す:
正規分布に従う変数の平方はGammaDistributionの特殊ケースであり,ChiSquareDistributionの特殊ケースでもある:
LaplaceDistributionは正規分布とRayleighDistributionの母数混合分布である:
StudentTDistributionは正規分布とGammaDistributionの母数混合分布である:
LevyDistributionは正規分布を変換したものである:
正規分布はタイプ3のピアソン分布(PearsonDistribution)の特殊ケースである:
正規分布はStableDistributionである:
正規分布はBinormalDistributionの周辺分布である:
正規分布はMultinormalDistributionの周辺分布である:
NormalDistributionはMultinormalDistributionから得ることができる:
StudentTDistributionはNormalDistributionとChiSquareDistributionから得られる:
NoncentralStudentTDistributionはNormalDistributionとChiSquareDistributionから得られる:
VarianceGammaDistributionはGammaDistributionと正規分布から得ることができる:
考えられる問題 (2)
テキスト
Wolfram Research (2007), NormalDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/NormalDistribution.html (2016年に更新).
CMS
Wolfram Language. 2007. "NormalDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/NormalDistribution.html.
APA
Wolfram Language. (2007). NormalDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NormalDistribution.html