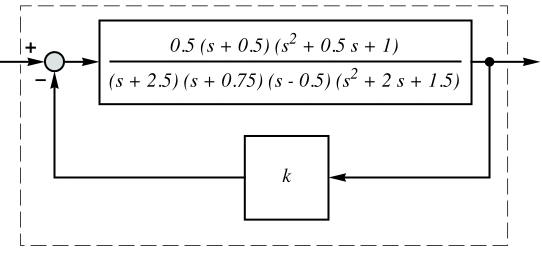
RootLocusPlot
RootLocusPlot[lsys,{k,kmin,kmax}]
線形時間不変系 lsys の,パラメータ k が kmin から kmaxまでの根軌跡プロットを生成する.
詳細とオプション



- RootLocusPlotは k の値の範囲で閉ループ系の極の位置をプロットする.
- RootLocusPlotは,事実上Blockを使って,パラメータ k を局所的なものとして扱う.
- 系のモデル lsys はStateSpaceModelまたはTransferFunctionModelである.
- RootLocusPlotでは Graphicsと同じオブションに次の追加・変更を加えたものが使える. [全オプションのリスト]
-
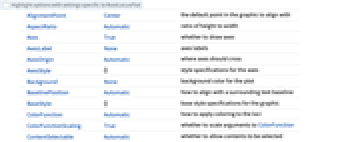
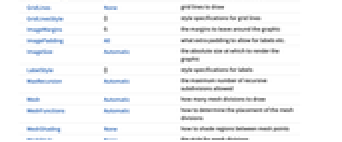
Axes True 座標軸を描くか描かないか ColorFunction Automatic 軌跡にどのように色付けするか ColorFunctionScaling True ColorFunctionへの引数をスケールするかどうか EvaluationMonitor None パラメータを評価するたびに評価する式 Exclusions Automatic 除外するパラメータの値 ExclusionsStyle None 除外された点の場所に何を描くか FeedbackType "Negative" フィードバックのタイプ MaxRecursion Automatic 使用できる再帰分割の最大数 Mesh Automatic 描くメッシュ区切りの数 MeshFunctions Automatic メッシュ区切りの配置の決め方 MeshShading None メッシュ点の間の領域の陰影付けをどうするか MeshStyle None メッシュ区切りのスタイル Method Automatic 軌跡を決めるメソッド PerformanceGoal $PerformanceGoal パフォーマンスのどの面について最適化するか PlotPoints Automatic サンプルパラメータ点の最初の数 PlotRange Automatic 含める値の範囲 PlotRangeClipping True プロット範囲で切り取るかどうか PlotStyle Automatic 軌跡のスタイルを指定するグラフィックス指示子 PlotTheme $PlotTheme プロットの全体的なテーマ PoleZeroMarkers Automatic 極と零点のマーカー RegionFunction (True&) ある点を含めるかどうかの決め方 PlotLegends None 根基積の凡例 WorkingPrecision MachinePrecision 内部計算の精度 - RootLocusPlotはMethodオプションを使って根軌跡の計算に使われるメソッドを指定する.
- Method->"GenericSolve"の設定では,軌跡はサンプル点の根を計算しそれをソートして決定される.
- Method->"NDSolve"とすると,RootLocusPlotはNDSolveを使って微分方程式
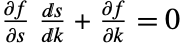 を解く.ただし,
を解く.ただし,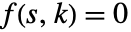 は閉ループ系の特性方程式であり,
は閉ループ系の特性方程式であり,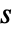 は複素変数である.
は複素変数である. - Method->{"NDSolve",opt1->val1,opt2->val2,…}は指定されたNDSolveオプションを使う.
- k の特定の値に対する閉ループの極は,Mesh,MeshFunctions,MeshStyleに適した設定でプロットすることができる.
- 閉ループの極だけでなく開ループの極および零点のマーカーもPoleZeroMarkersオプションの設定値で指定することができる.
- RegionFunctionの引数は,x,y,k である.
全オプションのリスト


例題
すべて開くすべて閉じる
Wolfram Research (2010), RootLocusPlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/RootLocusPlot.html (2014年に更新).
テキスト
Wolfram Research (2010), RootLocusPlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/RootLocusPlot.html (2014年に更新).
CMS
Wolfram Language. 2010. "RootLocusPlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/RootLocusPlot.html.
APA
Wolfram Language. (2010). RootLocusPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RootLocusPlot.html