SingularValuePlot
SingularValuePlot[lsys]
系 lsys の伝達関数の特異値のプロットを与える.
SingularValuePlot[lsys,{ωmin,ωmax}]
ωmin から ωmax までの周波数範囲のプロットを与える.
SingularValuePlot[expr,{ω,ωmin,ωmax}]
変数 ω を使って expr をプロットする.
詳細とオプション

- 系 lsys は,ディスクリプタ系と遅延系を含むTransferFunctionModelまたはStateSpaceModelである.
- 対応する伝達関数
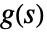 を持つ系 lsys について,次の式をプロットすることができる.
を持つ系 lsys について,次の式をプロットすることができる. -
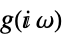
連続時間系 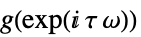
サンプル時間が 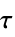 の離散時間系
の離散時間系 - SingularValuePlotは,事実上Blockを使って,ω を局所的なものとして扱う.
- SingularValuePlotにはPlotのオプションと同じものに以下の追加・変更を加えたものが使える. [全オプションのリスト]
-
SamplingPeriod None サンプリング周期 ScalingFunctions {"Log10","dB"} スケーリング関数 Tolerance 0 特異値を計算する際の許容度 - スケーリング関数はScalingFunctions->{freqscale,magscale}で指定できる.
- 周波数のスケール freqscaleは"Log10"あるいは"Linear"である.これはそれぞれ基底が10の対数スケールと線形スケールに相当する.
- ゲインスケール magscale は,ゲインのデシベル値と絶対値にそれぞれ相当する"dB"か"Absolute"のいずれかである.
全オプションのリスト
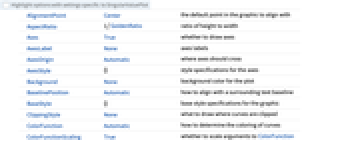

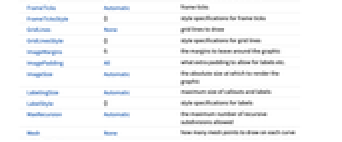

例題
すべて開くすべて閉じるスコープ (7)
SingularValuePlotはすべての特異値を示す:
オプション (16)
CoordinatesToolOptions (3)
PlotLegends (4)
Wolfram Research (2010), SingularValuePlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/SingularValuePlot.html (2014年に更新).
テキスト
Wolfram Research (2010), SingularValuePlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/SingularValuePlot.html (2014年に更新).
CMS
Wolfram Language. 2010. "SingularValuePlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/SingularValuePlot.html.
APA
Wolfram Language. (2010). SingularValuePlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SingularValuePlot.html