Tetrahedron
表示具有单位边长,以原点为中心的正四面体.
Tetrahedron[l]
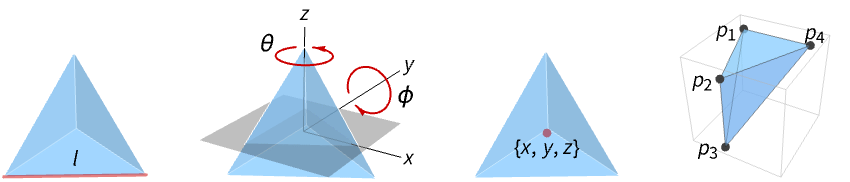
表示边长为 l 的四面体.
Tetrahedron[{θ,ϕ},…]
表示关于 z 轴旋转 θ 角和关于 y 轴旋转 ϕ 角的四面体.
Tetrahedron[{x,y,z},…]
表示中心在 {x,y,z} 的四面体.
Tetrahedron[{p1,p2,p3,p4}]
表示一个一般实心的四面体,四个角分别为 p1,p2,p3 和 p4.
Tetrahedron[{{p1,1,p1,2,p1,3,p1,4},{p2,1,…},…}]
表示一个四面体的集合.
更多信息和选项

- Tetrahedron 也被成为正四面体或三棱锥.
- Tetrahedron 可被当作几何区域和图元使用.
- Tetrahedron[] 等价于 Tetrahedron[{0,0,0},1].
- Tetrahedron[l] 等价于 Tetrahedron[{0,0,0},l].
- Tetrahedron[{p1,p2,p3,p4}] 代表由所有端点 pi 的凸组合构成的区域,
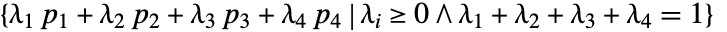 .
. - CanonicalizePolyhedron 可用于把四面体转换为明确的 Polyhedron 对象.
- Tetrahedron 可以用在 Graphics3D.
- 在图形中,点和边长可以是 Scaled 和 Dynamic 表达式.
- 影响图形渲染的指导指令有 FaceForm,EdgeForm, Opacity, Texture 以及颜色.
- 以下选项和设置可以在图形中使用:
-
VertexColors Automatic 将被插值的顶点颜色 VertexNormals Automatic 浓淡处理的有效顶点法线 VertexTextureCoordinates None 纹理的坐标
范例
打开所有单元关闭所有单元范围 (19)
图形 (9)
样式 (3)
坐标 (3)
区域 (10)
在四面体上 Integrate:
应用 (5)
属性和关系 (8)
TriangulateMesh 可用来把体积网格分解成四面体:
使用选项例如 MaxCellMeasure 来控制四面体的个数:
Tetrahedron 是 Simplex 的特例:
ImplicitRegion 可代表任何 Tetrahedron 区域:
Tetrahedron 是它的顶点的凸组合集合:
Tetrahedron 的顶点可以用来形成一个 Circumsphere 的包围:
文本
Wolfram Research (2014),Tetrahedron,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Tetrahedron.html (更新于 2019 年).
CMS
Wolfram 语言. 2014. "Tetrahedron." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2019. https://reference.wolfram.com/language/ref/Tetrahedron.html.
APA
Wolfram 语言. (2014). Tetrahedron. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Tetrahedron.html 年