DiscreteLimit
✖
DiscreteLimit
更多信息和选项


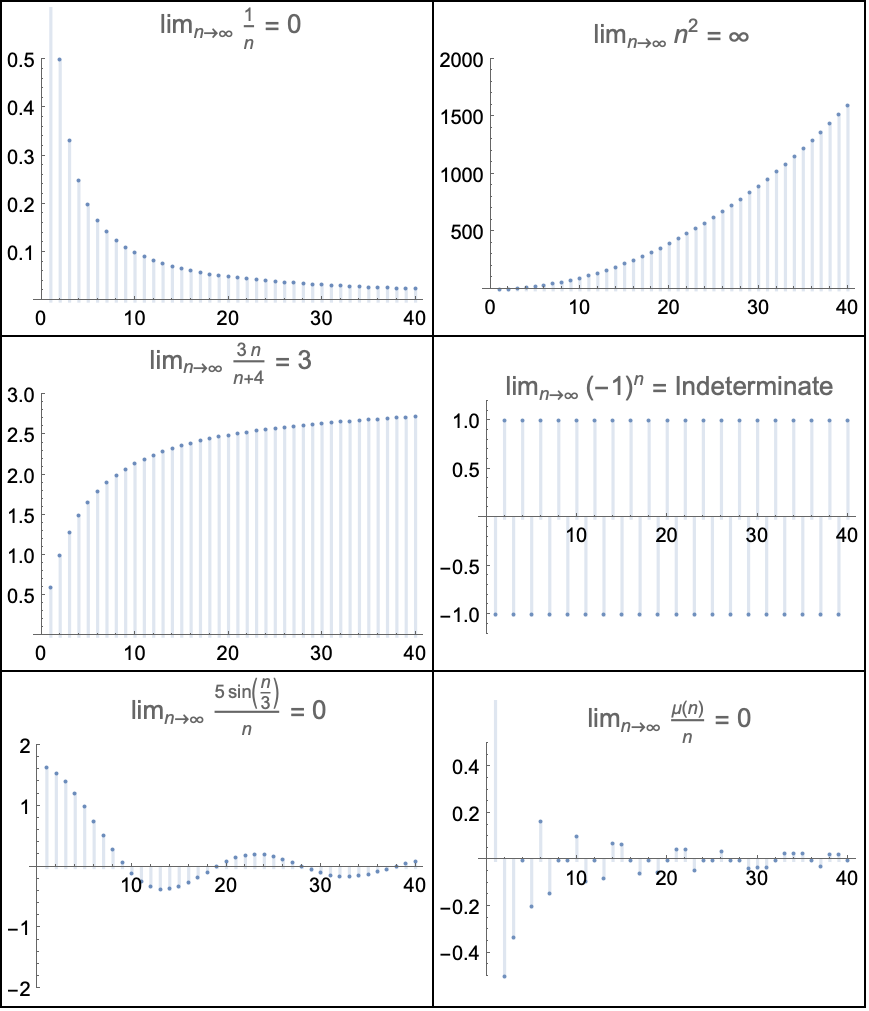
- DiscreteLimit 亦称为离散极限或整数上的极限.
- DiscreteLimit 计算序列 f 当变量 k 或 ki 变得任意大时的极限值.
- 可用
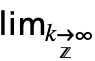 f 来输入 DiscreteLimit[f,k∞]. 可用
f 来输入 DiscreteLimit[f,k∞]. 可用  dlim
dlim 来输入模板
来输入模板 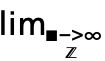 ,用
,用  把光标从底部移动到主体.
把光标从底部移动到主体. - 可用
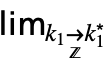 …
…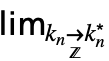 f 来输入 DiscreteLimit[f,{k1,…,kn}{
f 来输入 DiscreteLimit[f,{k1,…,kn}{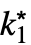 ,…,
,…,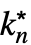 }].
}]. 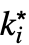 的极限值为 ±∞.
的极限值为 ±∞. - 对于有限值 f*:
-
DiscreteLimit[f,k∞]f* 对于每一个 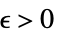 ,有一个
,有一个 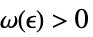 ,使得
,使得 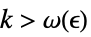 实质蕴涵
实质蕴涵 ![TemplateBox[{{{f, (, k, )}, -, {f, ^, *}}}, Abs]<epsilon TemplateBox[{{{f, (, k, )}, -, {f, ^, *}}}, Abs]<epsilon](Files/DiscreteLimit.zh/27.png)
DiscreteLimit[f,{k1,…,kn}{∞,…,∞}]f* 对于每一个 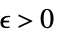 ,有一个
,有一个 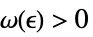 ,使得
,使得 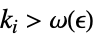 实质蕴涵
实质蕴涵 ![TemplateBox[{{{f, (, {{k, _, 1}, ,, ..., ,, {k, _, n}}, )}, -, {f, ^, *}}}, Abs]<epsilon TemplateBox[{{{f, (, {{k, _, 1}, ,, ..., ,, {k, _, n}}, )}, -, {f, ^, *}}}, Abs]<epsilon](Files/DiscreteLimit.zh/31.png)
- DiscreteLimit[f[k],k-∞] 等价于 DiscreteLimit[f[-l],l∞] 等.
- 当可以证明极限不存在时,DiscreteLimit 返回 Indeterminate,如果无法找到极限,则不进行计算,直接返回.
- 可以给出下列选项:
-
Assumptions $Assumptions 对参数的假设 GenerateConditions Automatic 是否为参数生成条件 Method Automatic 所用的方法 PerformanceGoal "Quality" 优化的目标 - GenerateConditions 的可能设置包括:
-
Automatic 只汇报非通用条件 True 汇报所有条件 False 不汇报条件 None 如果需要条件,则不进行计算,直接返回 - PerformanceGoal 的可能设置包括 $PerformanceGoal、"Quality" 和 "Speed". 如果设置为 "Quality", DiscreteLimit 通常能求解更多问题或产生更简单的结果,但会需要更多时间和内存.
范例
打开所有单元关闭所有单元基本范例 (4)常见实例总结
https://wolfram.com/xid/0enzj0dsy-dab3pa
https://wolfram.com/xid/0enzj0dsy-naxyuq
https://wolfram.com/xid/0enzj0dsy-zhoqg
https://wolfram.com/xid/0enzj0dsy-k3ivv
https://wolfram.com/xid/0enzj0dsy-e1mcaw
TraditionalForm 排版:
https://wolfram.com/xid/0enzj0dsy-e82anr
范围 (37)标准用法实例范围调查
基本用法 (4)
计算当 n 趋近于 Infinity 时序列的极限:
https://wolfram.com/xid/0enzj0dsy-hb5uiw
https://wolfram.com/xid/0enzj0dsy-jenjxu
计算当 n 趋近于 -Infinity 时序列的极限:
https://wolfram.com/xid/0enzj0dsy-et7bpy
https://wolfram.com/xid/0enzj0dsy-pukp4y
https://wolfram.com/xid/0enzj0dsy-g45pgr
初等函数序列 (7)
https://wolfram.com/xid/0enzj0dsy-lxbke9
https://wolfram.com/xid/0enzj0dsy-c6vm2a
https://wolfram.com/xid/0enzj0dsy-q2dwr
https://wolfram.com/xid/0enzj0dsy-g2hriz
https://wolfram.com/xid/0enzj0dsy-fxkte2
https://wolfram.com/xid/0enzj0dsy-ek16lf
https://wolfram.com/xid/0enzj0dsy-kox3rp
https://wolfram.com/xid/0enzj0dsy-fh66s0
https://wolfram.com/xid/0enzj0dsy-e5uei
https://wolfram.com/xid/0enzj0dsy-dm6ege
https://wolfram.com/xid/0enzj0dsy-lykjl
https://wolfram.com/xid/0enzj0dsy-yzua9
https://wolfram.com/xid/0enzj0dsy-8qd0z
https://wolfram.com/xid/0enzj0dsy-i4pw3x
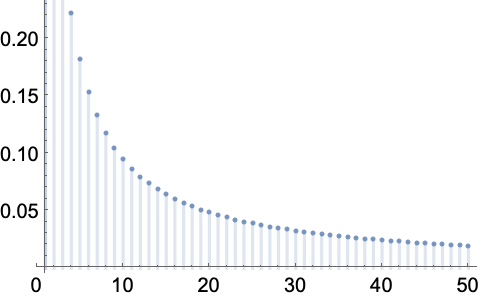
https://wolfram.com/xid/0enzj0dsy-bcko2g
https://wolfram.com/xid/0enzj0dsy-lnyf1f
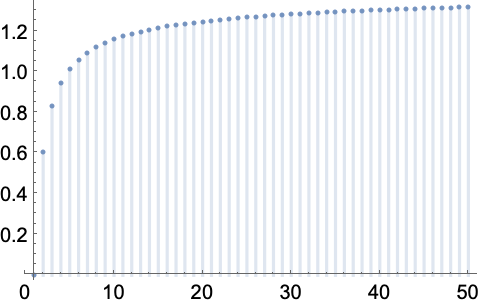
整数函数序列 (5)
https://wolfram.com/xid/0enzj0dsy-d8pfbn
涉及 FactorialPower 的序列的极限:
https://wolfram.com/xid/0enzj0dsy-ftvybu
https://wolfram.com/xid/0enzj0dsy-lmqwqq
涉及 Factorial 的序列的极限:
https://wolfram.com/xid/0enzj0dsy-b7gjcw
https://wolfram.com/xid/0enzj0dsy-dqkc2t
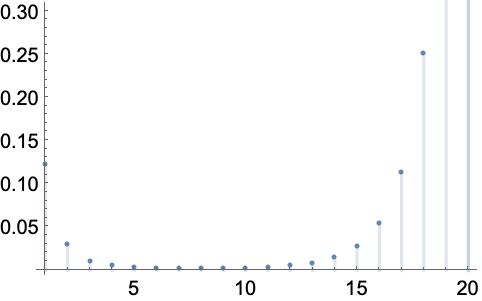
https://wolfram.com/xid/0enzj0dsy-9co6a
https://wolfram.com/xid/0enzj0dsy-ha08jt
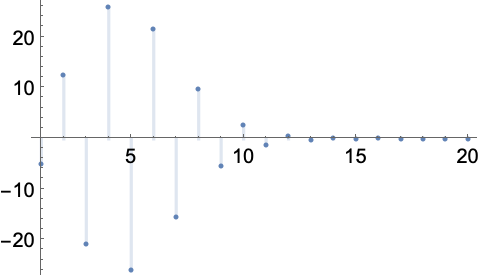
计算涉及 Fibonacci 和 LucasL 的序列的极限:
https://wolfram.com/xid/0enzj0dsy-bcqotc
https://wolfram.com/xid/0enzj0dsy-htkqx9
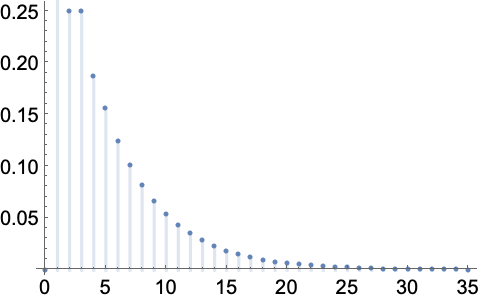
https://wolfram.com/xid/0enzj0dsy-2jx94
https://wolfram.com/xid/0enzj0dsy-fyr369
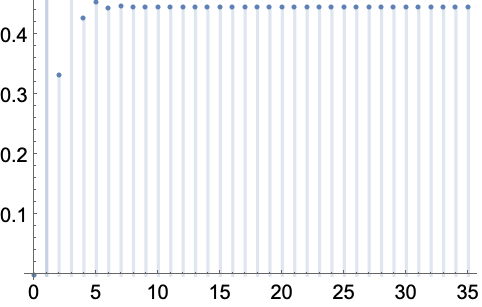
涉及 Pochhammer 的极限:
https://wolfram.com/xid/0enzj0dsy-8qnoq
交错序列 (3)
https://wolfram.com/xid/0enzj0dsy-l018j
https://wolfram.com/xid/0enzj0dsy-d9uwn4
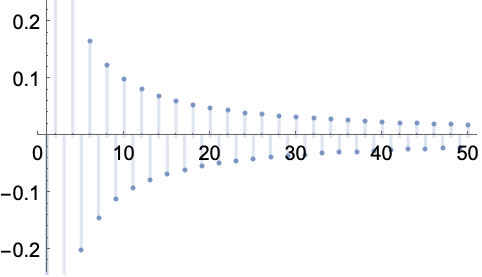
https://wolfram.com/xid/0enzj0dsy-jt1djy
https://wolfram.com/xid/0enzj0dsy-e3j59y
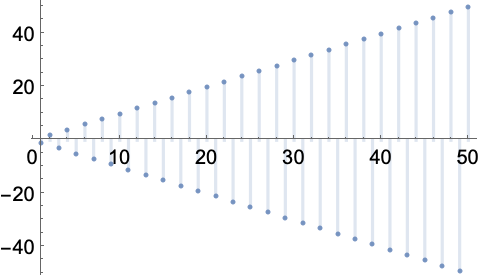
https://wolfram.com/xid/0enzj0dsy-c2a9wn
https://wolfram.com/xid/0enzj0dsy-k4obt0
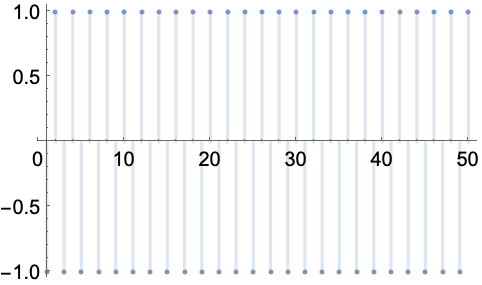
周期序列 (3)
https://wolfram.com/xid/0enzj0dsy-hug9t9
https://wolfram.com/xid/0enzj0dsy-gnytrw
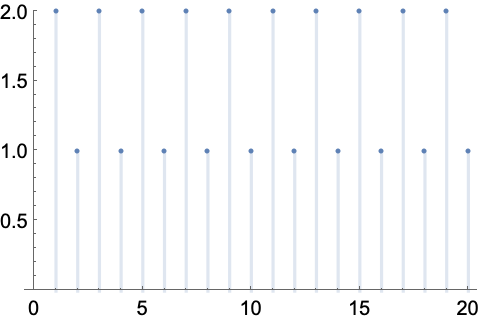
https://wolfram.com/xid/0enzj0dsy-pb2vbj
https://wolfram.com/xid/0enzj0dsy-bpl1lb
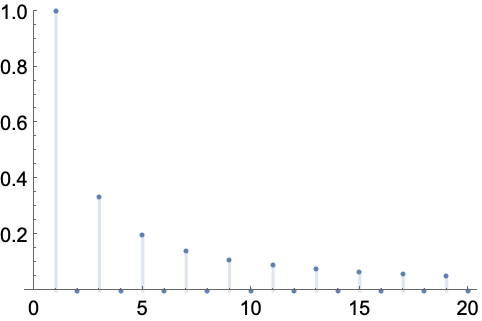
https://wolfram.com/xid/0enzj0dsy-cpqsv5
https://wolfram.com/xid/0enzj0dsy-k12ere
https://wolfram.com/xid/0enzj0dsy-d7z025
https://wolfram.com/xid/0enzj0dsy-k07f3o
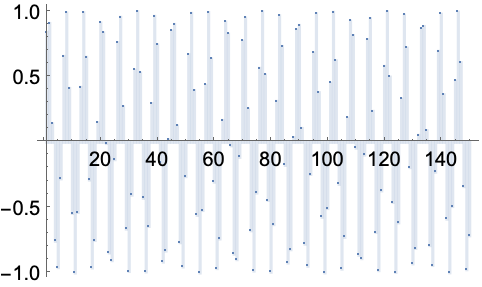
https://wolfram.com/xid/0enzj0dsy-lmhs11
https://wolfram.com/xid/0enzj0dsy-bzcdcc
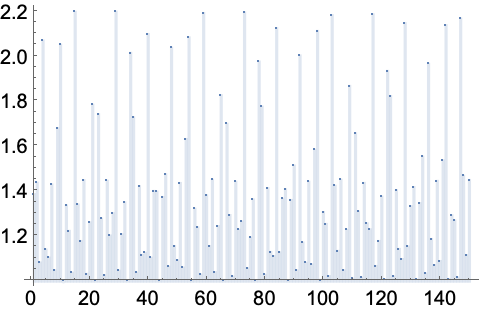
分段函数序列 (3)
https://wolfram.com/xid/0enzj0dsy-vznig
https://wolfram.com/xid/0enzj0dsy-tz15g
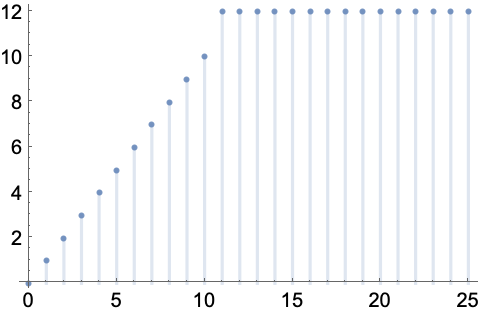
https://wolfram.com/xid/0enzj0dsy-xejfm
https://wolfram.com/xid/0enzj0dsy-m4nvru
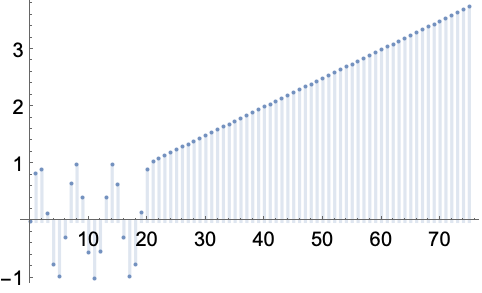
https://wolfram.com/xid/0enzj0dsy-d9ybuq
https://wolfram.com/xid/0enzj0dsy-skkms
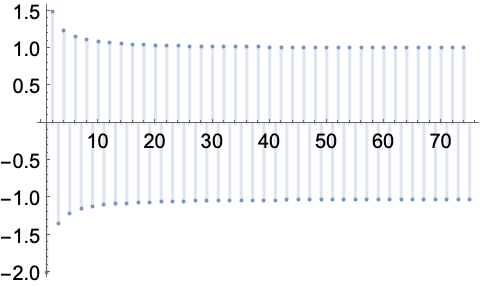
涉及 Floor 的极限:
https://wolfram.com/xid/0enzj0dsy-ccscxv
https://wolfram.com/xid/0enzj0dsy-00nnb5
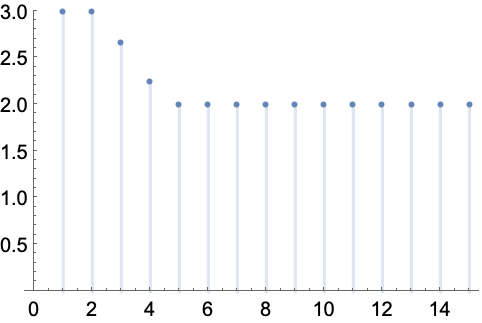
数论函数序列 (4)
计算涉及 Prime 的极限:
https://wolfram.com/xid/0enzj0dsy-c8zquf
https://wolfram.com/xid/0enzj0dsy-lasy8a
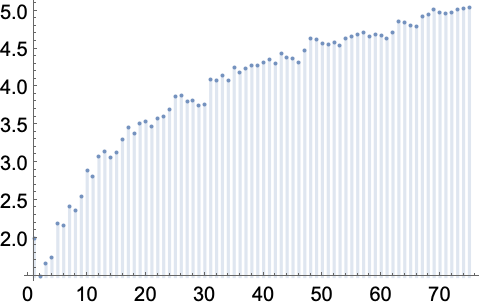
https://wolfram.com/xid/0enzj0dsy-kcv0us
https://wolfram.com/xid/0enzj0dsy-fq8b91
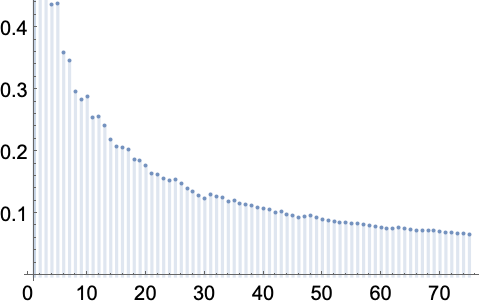
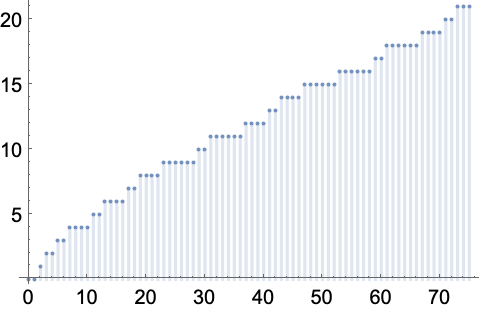
Prime 接近于 ![]() :
:
https://wolfram.com/xid/0enzj0dsy-fsldo
https://wolfram.com/xid/0enzj0dsy-v3pty
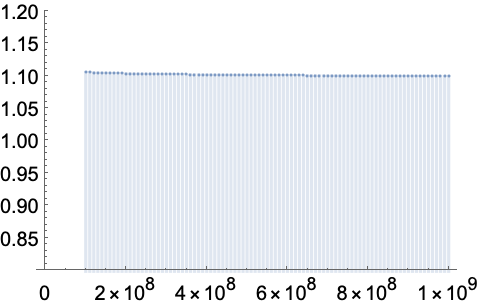
涉及 PrimePi 的极限:
https://wolfram.com/xid/0enzj0dsy-ctmzmi
https://wolfram.com/xid/0enzj0dsy-xsf9u
https://wolfram.com/xid/0enzj0dsy-7e7a
https://wolfram.com/xid/0enzj0dsy-b8nou9
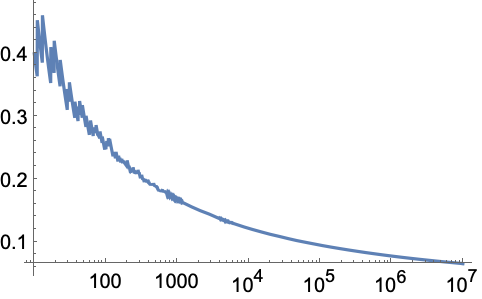
PrimePi 接近于 ![]() :
:
https://wolfram.com/xid/0enzj0dsy-fuinb4
https://wolfram.com/xid/0enzj0dsy-qbv5vf
涉及 PartitionsP 和 PartitionsQ 的极限:
https://wolfram.com/xid/0enzj0dsy-gv4ho
https://wolfram.com/xid/0enzj0dsy-evj3r
https://wolfram.com/xid/0enzj0dsy-fiya71
https://wolfram.com/xid/0enzj0dsy-mdx71
https://wolfram.com/xid/0enzj0dsy-cl8agc
https://wolfram.com/xid/0enzj0dsy-f1s6nn
https://wolfram.com/xid/0enzj0dsy-ie03pn
https://wolfram.com/xid/0enzj0dsy-jdmej6
嵌套和多变量序列 (2)
https://wolfram.com/xid/0enzj0dsy-b08k82
https://wolfram.com/xid/0enzj0dsy-bx7d8j
https://wolfram.com/xid/0enzj0dsy-icispr
https://wolfram.com/xid/0enzj0dsy-bhhc93
https://wolfram.com/xid/0enzj0dsy-2sbsbp
形式序列 (6)
计算涉及 Inactive 和的序列的极限:
https://wolfram.com/xid/0enzj0dsy-d6f62u
https://wolfram.com/xid/0enzj0dsy-f1dl7b
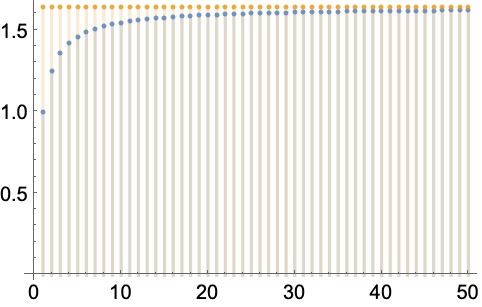
https://wolfram.com/xid/0enzj0dsy-byioul
https://wolfram.com/xid/0enzj0dsy-cysasg
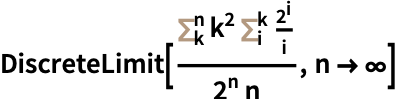
https://wolfram.com/xid/0enzj0dsy-gz13ht
Inactive 和的嵌套极限:
https://wolfram.com/xid/0enzj0dsy-ppyjdx
交换 DiscreteLimit 和 Sum 的顺序,分两步计算,获得同样的结果:
https://wolfram.com/xid/0enzj0dsy-w70qu
https://wolfram.com/xid/0enzj0dsy-gd8rz
涉及 Inactive 积的序列的极限:
https://wolfram.com/xid/0enzj0dsy-pc5wzj
https://wolfram.com/xid/0enzj0dsy-b9ctp5
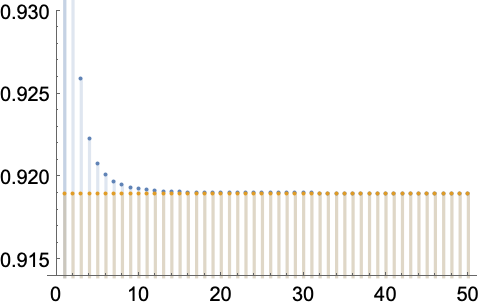
https://wolfram.com/xid/0enzj0dsy-hac34
Inactive 积的嵌套极限:
https://wolfram.com/xid/0enzj0dsy-dvd5oo
交换 DiscreteLimit 和 Product 的顺序,分两步计算,获得同样的结果:
https://wolfram.com/xid/0enzj0dsy-bksy8
https://wolfram.com/xid/0enzj0dsy-fg6rh3
涉及 Inactive 连分数的序列的极限:
https://wolfram.com/xid/0enzj0dsy-b24jat
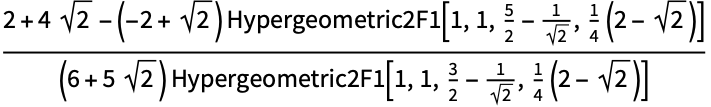
https://wolfram.com/xid/0enzj0dsy-fv0ch
Inactive 连分数的嵌套极限:
https://wolfram.com/xid/0enzj0dsy-er10r
通过运用 DiscreteLimit 和 ContinuedFractionK,分两步计算,获得同样的结果:
https://wolfram.com/xid/0enzj0dsy-blekj2
https://wolfram.com/xid/0enzj0dsy-ekenmi
选项 (6)各选项的常用值和功能
Assumptions (1)
GenerateConditions (3)
https://wolfram.com/xid/0enzj0dsy-6rd3fa
https://wolfram.com/xid/0enzj0dsy-lftbu6
https://wolfram.com/xid/0enzj0dsy-2lepxp
https://wolfram.com/xid/0enzj0dsy-14nrvk
https://wolfram.com/xid/0enzj0dsy-uhm6gw
当设置为 GenerateConditions->True 时,即便是非通用条件,也会汇报:
https://wolfram.com/xid/0enzj0dsy-291b1m
Method (1)
https://wolfram.com/xid/0enzj0dsy-gna87y
通过调用 Limit 获取同样的答案:
https://wolfram.com/xid/0enzj0dsy-jt0cjx
https://wolfram.com/xid/0enzj0dsy-eqc0mj
PerformanceGoal (1)
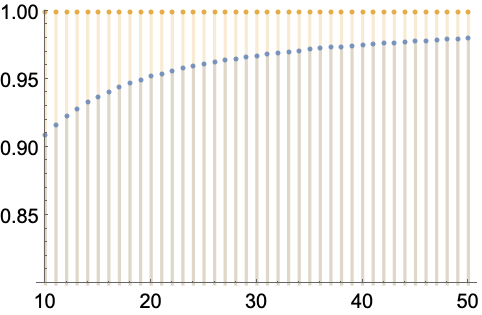
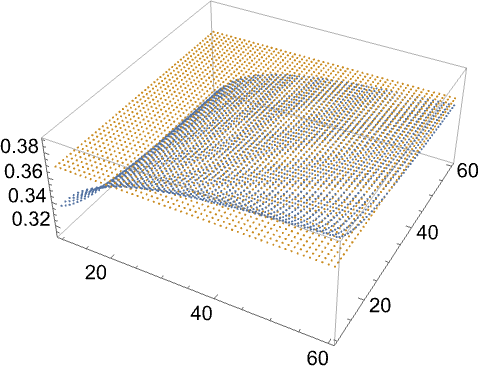
DiscreteLimit 计算周期为任意长度的序列的极限:
https://wolfram.com/xid/0enzj0dsy-i86kxj
https://wolfram.com/xid/0enzj0dsy-i9gq
用 PerformanceGoal 来避免此种花费时间较长的计算:
https://wolfram.com/xid/0enzj0dsy-byiylb
Method 选项会覆盖 PerformanceGoal:
https://wolfram.com/xid/0enzj0dsy-bh9kxc
应用 (35)用该函数可以解决的问题范例
几何极限 (3)
https://wolfram.com/xid/0enzj0dsy-twy612
https://wolfram.com/xid/0enzj0dsy-z6705c
https://wolfram.com/xid/0enzj0dsy-6uyygg
https://wolfram.com/xid/0enzj0dsy-qew1wi

https://wolfram.com/xid/0enzj0dsy-ytsz6j
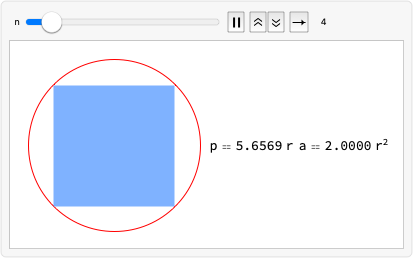

https://wolfram.com/xid/0enzj0dsy-x5wzmd
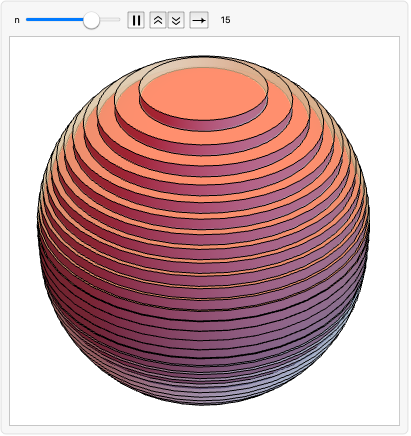
https://wolfram.com/xid/0enzj0dsy-oa8uz1
取当 n->Infinity 时的 DiscreteLimit 给出球的体积:
https://wolfram.com/xid/0enzj0dsy-lvmxv2
https://wolfram.com/xid/0enzj0dsy-to8z2u
https://wolfram.com/xid/0enzj0dsy-z9ud2d

https://wolfram.com/xid/0enzj0dsy-206nof
https://wolfram.com/xid/0enzj0dsy-gbe5lc
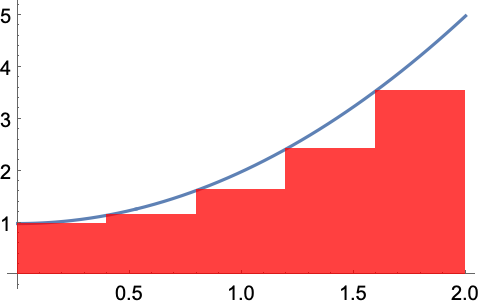
https://wolfram.com/xid/0enzj0dsy-d8rf0v
https://wolfram.com/xid/0enzj0dsy-blqncc
用 DiscreteLimit 获取精确答案:
https://wolfram.com/xid/0enzj0dsy-m82y4
用 Integrate 直接获得同样的面积:
https://wolfram.com/xid/0enzj0dsy-nkh41k

https://wolfram.com/xid/0enzj0dsy-g7o292
https://wolfram.com/xid/0enzj0dsy-g0awiw
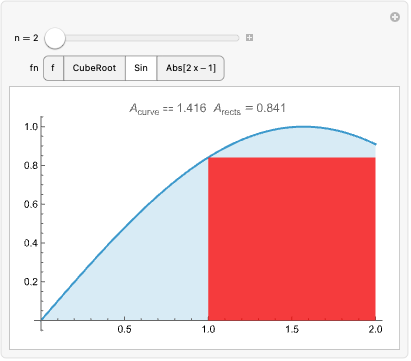
和与积 (6)
https://wolfram.com/xid/0enzj0dsy-e7wetu
用 Sum 获得同样的答案:
https://wolfram.com/xid/0enzj0dsy-bucem8
https://wolfram.com/xid/0enzj0dsy-2g43zd
https://wolfram.com/xid/0enzj0dsy-cusunh
https://wolfram.com/xid/0enzj0dsy-gj6a2w
用 Sum 直接计算结果:
https://wolfram.com/xid/0enzj0dsy-tmwr9b
https://wolfram.com/xid/0enzj0dsy-ouhy30
https://wolfram.com/xid/0enzj0dsy-e5njya
用 SumConvergence 和 Sum 确认级数是发散的:
https://wolfram.com/xid/0enzj0dsy-gkodeu
https://wolfram.com/xid/0enzj0dsy-ddrpmw
用 Regularization 获取级数的阿贝尔和:
https://wolfram.com/xid/0enzj0dsy-jow48n
https://wolfram.com/xid/0enzj0dsy-y29fc

https://wolfram.com/xid/0enzj0dsy-z7xm9
用 Sum 直接获取同样的答案:
https://wolfram.com/xid/0enzj0dsy-x7fhu
https://wolfram.com/xid/0enzj0dsy-foynmc
用 Product 获取同样的答案:
https://wolfram.com/xid/0enzj0dsy-enkto5
https://wolfram.com/xid/0enzj0dsy-s9t
https://wolfram.com/xid/0enzj0dsy-knb
https://wolfram.com/xid/0enzj0dsy-7uksox
级数收敛 (4)
https://wolfram.com/xid/0enzj0dsy-e3ja4c
计算该级数的 DiscreteRatio:
https://wolfram.com/xid/0enzj0dsy-or9ve
https://wolfram.com/xid/0enzj0dsy-gw0z8n
用 SumConvergence 验证结果:
https://wolfram.com/xid/0enzj0dsy-dvwrjt
https://wolfram.com/xid/0enzj0dsy-dg9vkx
https://wolfram.com/xid/0enzj0dsy-dbdj3t
用 SumConvergence 验证结果:
https://wolfram.com/xid/0enzj0dsy-j6uqov
用 Raabe 检验法来检验一般项由下式给出的级数的收敛性:
https://wolfram.com/xid/0enzj0dsy-hlfofg
Raabe 检验法在此是适用的,因为比例检验法的结果不确定:
https://wolfram.com/xid/0enzj0dsy-jda5ib
https://wolfram.com/xid/0enzj0dsy-1au62y
用 SumConvergence 验证结果:
https://wolfram.com/xid/0enzj0dsy-i6d07k
https://wolfram.com/xid/0enzj0dsy-btg6ia
https://wolfram.com/xid/0enzj0dsy-dnf8s5
用 SumConvergence 验证结果:
https://wolfram.com/xid/0enzj0dsy-f4qaev
经典定义 (3)
https://wolfram.com/xid/0enzj0dsy-ciuuy
https://wolfram.com/xid/0enzj0dsy-jx1tfs
https://wolfram.com/xid/0enzj0dsy-hj4723
用 Reduce 显示对于所有的 n>=12,定义成立:
https://wolfram.com/xid/0enzj0dsy-iej994
用 DiscretePlot 验证结果:
https://wolfram.com/xid/0enzj0dsy-b8qjep
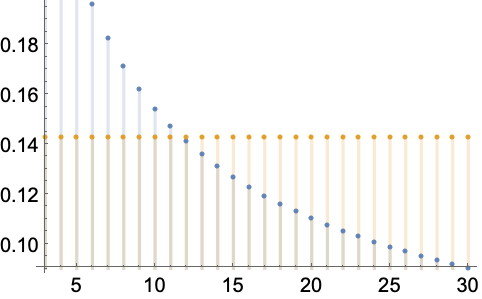
证明下列序列发散于 Infinity,并用 M=35 检验经典定义:
https://wolfram.com/xid/0enzj0dsy-jnjv3a
https://wolfram.com/xid/0enzj0dsy-bdqyd
https://wolfram.com/xid/0enzj0dsy-hpzwn8
用 Reduce 显示对于所有的 n >= 10,定义成立:
https://wolfram.com/xid/0enzj0dsy-czhyaa
用 DiscretePlot 验证结果:
https://wolfram.com/xid/0enzj0dsy-dvwf9p
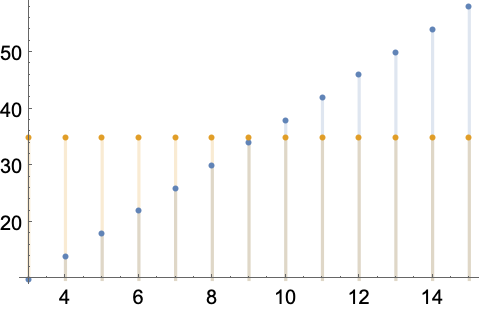
https://wolfram.com/xid/0enzj0dsy-j3gxce
https://wolfram.com/xid/0enzj0dsy-iasd6p
https://wolfram.com/xid/0enzj0dsy-ozkhdz
https://wolfram.com/xid/0enzj0dsy-fprcs5
https://wolfram.com/xid/0enzj0dsy-330hra
https://wolfram.com/xid/0enzj0dsy-xj1erx
https://wolfram.com/xid/0enzj0dsy-j5vin9
https://wolfram.com/xid/0enzj0dsy-emvke1
https://wolfram.com/xid/0enzj0dsy-d6xpgk
https://wolfram.com/xid/0enzj0dsy-4mfaij
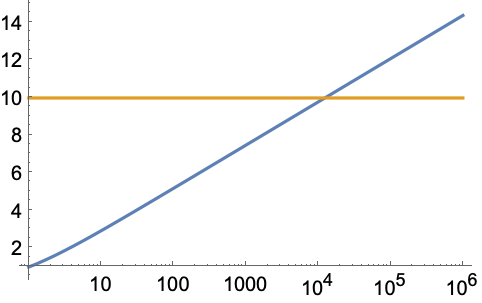
递归序列 (3)
计算用 RSolveValue 指定的非线性递归序列的极限:
https://wolfram.com/xid/0enzj0dsy-byuq03
https://wolfram.com/xid/0enzj0dsy-hv9hqo
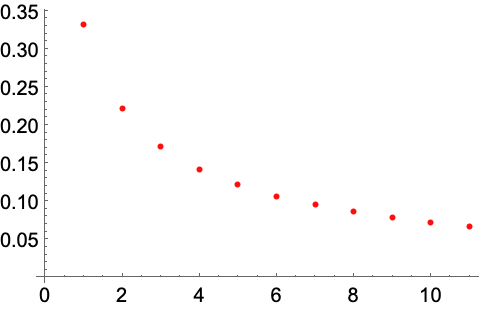
计算用 RSolveValue 指定的三角递归序列的极限:
https://wolfram.com/xid/0enzj0dsy-i1f8hp
https://wolfram.com/xid/0enzj0dsy-g2hnhx
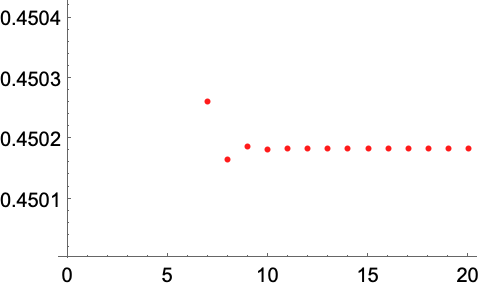
https://wolfram.com/xid/0enzj0dsy-0sez2
https://wolfram.com/xid/0enzj0dsy-k9i8af
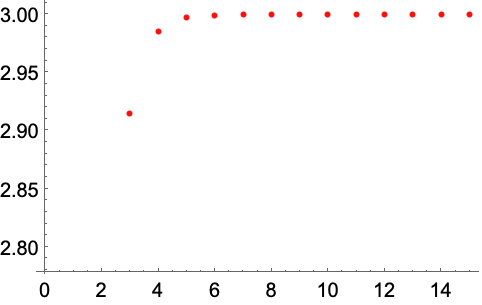
数学常数 (5)
https://wolfram.com/xid/0enzj0dsy-oeung
用 Sum 的极限计算 ![]() 的值:
的值:
https://wolfram.com/xid/0enzj0dsy-eads7b
https://wolfram.com/xid/0enzj0dsy-4btt0
用序列的极限计算 EulerGamma:
https://wolfram.com/xid/0enzj0dsy-peilrk
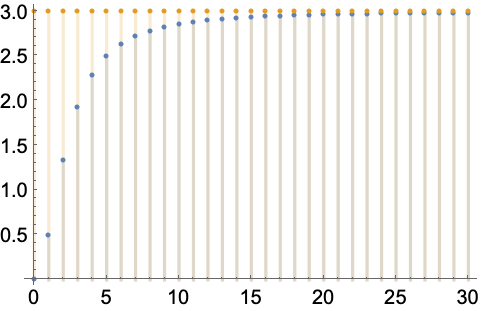
用涉及 Fibonacci 的序列计算黄金比例:
https://wolfram.com/xid/0enzj0dsy-dvtcgb
https://wolfram.com/xid/0enzj0dsy-c5nne
数学函数 (2)
https://wolfram.com/xid/0enzj0dsy-mx9e9
用序列的极限表示 Log[x]:
https://wolfram.com/xid/0enzj0dsy-c3ferw
Stolz–Cesàro 定理 (2)
Stolz–Cesàro 定理是 L'Hôpital 规则的离散版本,在合适的条件下可用于计算序列之比的极限. 该定理指出:

https://wolfram.com/xid/0enzj0dsy-e66sks
https://wolfram.com/xid/0enzj0dsy-kd51q
https://wolfram.com/xid/0enzj0dsy-kwn30q
https://wolfram.com/xid/0enzj0dsy-fddq9l
用 DiscreteLimit 直接获取同样的结果:
https://wolfram.com/xid/0enzj0dsy-by2rl4
https://wolfram.com/xid/0enzj0dsy-b6go6h
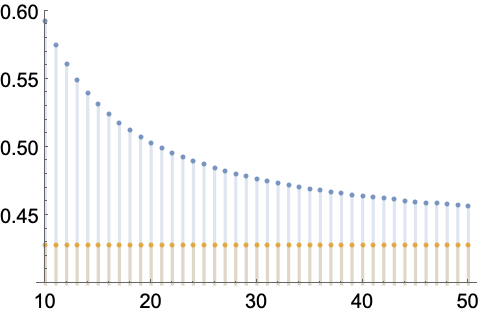
https://wolfram.com/xid/0enzj0dsy-1b2l
https://wolfram.com/xid/0enzj0dsy-g24mng
https://wolfram.com/xid/0enzj0dsy-c7rbsy
用 DiscreteLimit 直接获取同样的结果:
https://wolfram.com/xid/0enzj0dsy-l44eop
https://wolfram.com/xid/0enzj0dsy-dvkd59
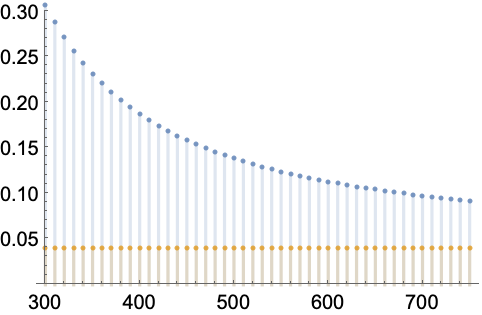
计算复杂性 (3)
一个算法运行时间函数 ![]() 被认为是 "little-o of
被认为是 "little-o of ![]() ",写作
",写作 ![]() ,如果
,如果 ![]() :
:
https://wolfram.com/xid/0enzj0dsy-mlj236
同样,![]() 还被认为是 "little-omega of
还被认为是 "little-omega of ![]() ",写作
",写作 ![]() ,如果
,如果 ![]() :
:
https://wolfram.com/xid/0enzj0dsy-ofku20
https://wolfram.com/xid/0enzj0dsy-c8jqd3
https://wolfram.com/xid/0enzj0dsy-dy4l4s
https://wolfram.com/xid/0enzj0dsy-bv5n1w
因此,![]() 和
和 ![]() 在算法运行时间空间 (runtime space) 上定义了部分关系:
在算法运行时间空间 (runtime space) 上定义了部分关系:
https://wolfram.com/xid/0enzj0dsy-17pwac
对于较大的输入,如果与 ![]() 关联的算法要比与
关联的算法要比与 ![]() 关联的算法快的多,则
关联的算法快的多,则 ![]() :
:
https://wolfram.com/xid/0enzj0dsy-sh3ntl
https://wolfram.com/xid/0enzj0dsy-y0dogg
https://wolfram.com/xid/0enzj0dsy-3r0jej
一个算法运行时间函数 ![]() 被认为是 "big-theta of
被认为是 "big-theta of ![]() ",写作
",写作 ![]() ,如果下式成立:
,如果下式成立:
https://wolfram.com/xid/0enzj0dsy-upxsuv
https://wolfram.com/xid/0enzj0dsy-nvt8l4
https://wolfram.com/xid/0enzj0dsy-uk9w7i
https://wolfram.com/xid/0enzj0dsy-elt437
对于算法运行时间,![]() 必须是一个正的有限大的数字,所以每个多项式算法都可写为
必须是一个正的有限大的数字,所以每个多项式算法都可写为 ![]() :
:
https://wolfram.com/xid/0enzj0dsy-bbqvi9
因此,在确定大型输入的运行时间时,只有多项式中的首项很重要:
https://wolfram.com/xid/0enzj0dsy-bb05nv
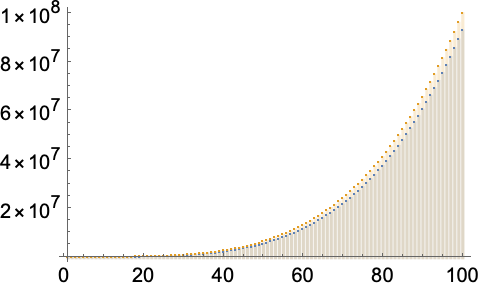
https://wolfram.com/xid/0enzj0dsy-jnyodd
https://wolfram.com/xid/0enzj0dsy-cd00m5
https://wolfram.com/xid/0enzj0dsy-dvpg6x
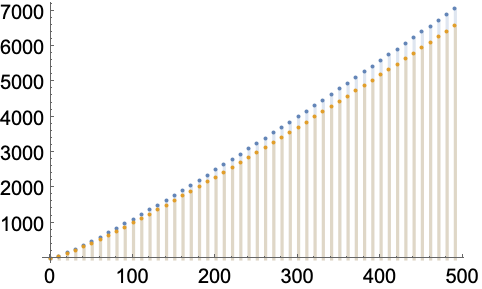
均匀收敛 (2)
https://wolfram.com/xid/0enzj0dsy-gg43gi
https://wolfram.com/xid/0enzj0dsy-0x579
https://wolfram.com/xid/0enzj0dsy-5dqqz0
https://wolfram.com/xid/0enzj0dsy-d3t774
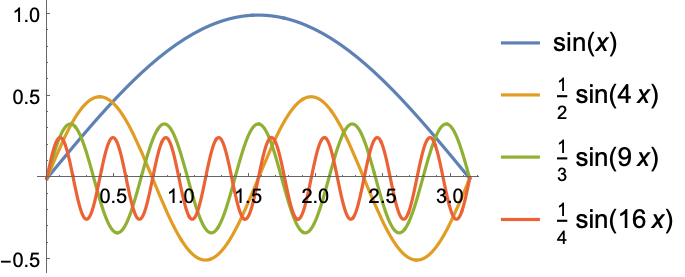
https://wolfram.com/xid/0enzj0dsy-k91wt
https://wolfram.com/xid/0enzj0dsy-bayvi0
https://wolfram.com/xid/0enzj0dsy-j49rv9
https://wolfram.com/xid/0enzj0dsy-tisggo
https://wolfram.com/xid/0enzj0dsy-iskd42
https://wolfram.com/xid/0enzj0dsy-1dyya
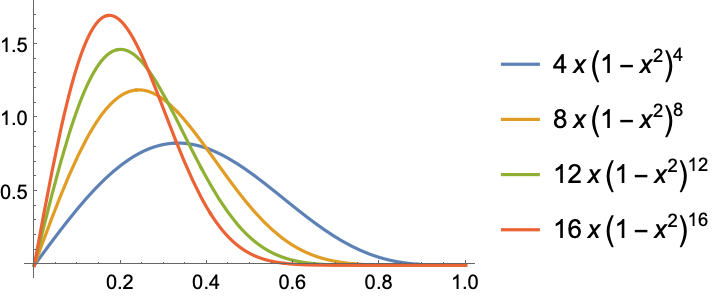
https://wolfram.com/xid/0enzj0dsy-j254qv
https://wolfram.com/xid/0enzj0dsy-oqww1
其它应用 (2)
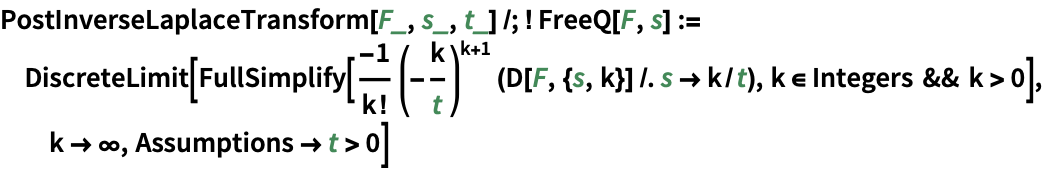
https://wolfram.com/xid/0enzj0dsy-4xcbf
https://wolfram.com/xid/0enzj0dsy-38yi6
用 InverseLaplaceTransform 获取同样的结果:
https://wolfram.com/xid/0enzj0dsy-bam80n
https://wolfram.com/xid/0enzj0dsy-dcxr8

https://wolfram.com/xid/0enzj0dsy-byjhvn
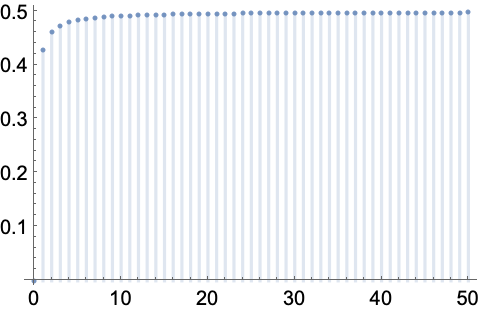
随机变量序列的概率分布的极限(如果存在)称为渐进分布. 用二项式分布序列的渐进分布获得泊松分布,其中均值 λ、概率和试验次数的乘积保持不变:
https://wolfram.com/xid/0enzj0dsy-y0zk1
https://wolfram.com/xid/0enzj0dsy-lfwa7w
验证这是 PoissonDistribution 的 PDF:
https://wolfram.com/xid/0enzj0dsy-dyers1
绘制 λ=8 及 n 取不同值时的分布. 注意 k>n 时 PDF 为零:

https://wolfram.com/xid/0enzj0dsy-88o288
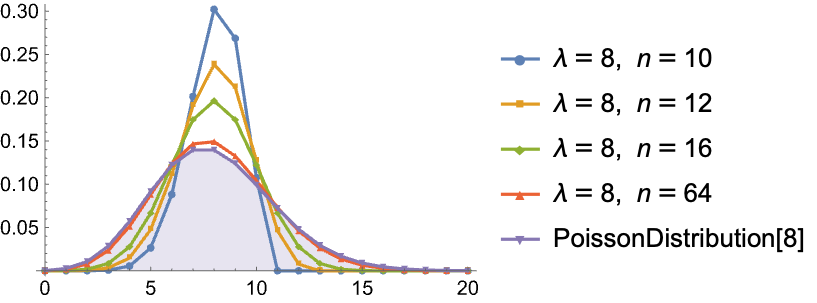
属性和关系 (15)函数的属性及与其他函数的关联
https://wolfram.com/xid/0enzj0dsy-h9ydrm
https://wolfram.com/xid/0enzj0dsy-rznz43
如果 f 和 g 的极限为有限值,则 DiscreteLimit 在和上满足分配律:
https://wolfram.com/xid/0enzj0dsy-hapf7s
https://wolfram.com/xid/0enzj0dsy-ki9asl
https://wolfram.com/xid/0enzj0dsy-hoyphw
如果 f 和 g 的极限为有限值,则 DiscreteLimit 在乘积上满足分配律:
https://wolfram.com/xid/0enzj0dsy-c04ob7
https://wolfram.com/xid/0enzj0dsy-o9zq47
https://wolfram.com/xid/0enzj0dsy-by5j87
https://wolfram.com/xid/0enzj0dsy-j63e3f
https://wolfram.com/xid/0enzj0dsy-eh42g1
https://wolfram.com/xid/0enzj0dsy-gpdhh3
https://wolfram.com/xid/0enzj0dsy-heu2u0
https://wolfram.com/xid/0enzj0dsy-f1rykc
https://wolfram.com/xid/0enzj0dsy-h8v0uu
https://wolfram.com/xid/0enzj0dsy-0bv4os
https://wolfram.com/xid/0enzj0dsy-zwywc
https://wolfram.com/xid/0enzj0dsy-wbzb2v
https://wolfram.com/xid/0enzj0dsy-zocgex
https://wolfram.com/xid/0enzj0dsy-b1meus
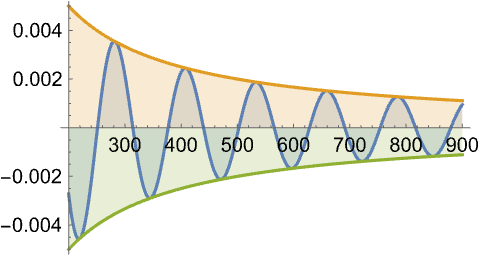
Stolz–Cesàro 规则可被原来求两个序列的比的极限:
https://wolfram.com/xid/0enzj0dsy-2m2ut
https://wolfram.com/xid/0enzj0dsy-cueok0
https://wolfram.com/xid/0enzj0dsy-byrenx
https://wolfram.com/xid/0enzj0dsy-d97ufy
https://wolfram.com/xid/0enzj0dsy-b3w8pq
如果 Limit 存在,则 DiscreteLimit 也存在,且它们的值相同:
https://wolfram.com/xid/0enzj0dsy-djj1nf
https://wolfram.com/xid/0enzj0dsy-tlom4
https://wolfram.com/xid/0enzj0dsy-bb2v
https://wolfram.com/xid/0enzj0dsy-58ji5s
https://wolfram.com/xid/0enzj0dsy-34gpyb
https://wolfram.com/xid/0enzj0dsy-qtl6qs
https://wolfram.com/xid/0enzj0dsy-uu7jv3
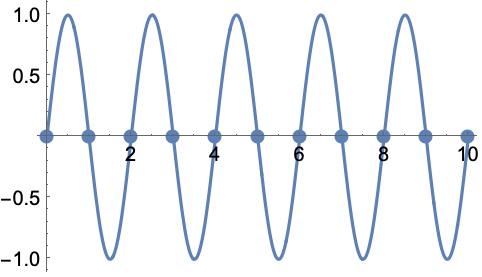
如果 DiscreteLimit 存在,则 DiscreteMaxLimit 也存在,且它们的值相同:
https://wolfram.com/xid/0enzj0dsy-ke9m6n
https://wolfram.com/xid/0enzj0dsy-fn6uxd
https://wolfram.com/xid/0enzj0dsy-il9la
如果 DiscreteLimit 存在,则 DiscreteMinLimit也存在,且它们的值相同:
https://wolfram.com/xid/0enzj0dsy-jir5ws
https://wolfram.com/xid/0enzj0dsy-jj4e7e
https://wolfram.com/xid/0enzj0dsy-elmh30
https://wolfram.com/xid/0enzj0dsy-cakso2
https://wolfram.com/xid/0enzj0dsy-fc8lse
https://wolfram.com/xid/0enzj0dsy-bnjdmp
https://wolfram.com/xid/0enzj0dsy-d0xkht
https://wolfram.com/xid/0enzj0dsy-fes1yz
https://wolfram.com/xid/0enzj0dsy-dsqfi5
https://wolfram.com/xid/0enzj0dsy-dl81lk
https://wolfram.com/xid/0enzj0dsy-ko2dnd
https://wolfram.com/xid/0enzj0dsy-hstyi1
https://wolfram.com/xid/0enzj0dsy-lb879
序列的极限通过终值定理与其 ZTransform 相关:
https://wolfram.com/xid/0enzj0dsy-cuuulh
https://wolfram.com/xid/0enzj0dsy-i28hy9
Wolfram Research (2017),DiscreteLimit,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DiscreteLimit.html.文本
Wolfram Research (2017),DiscreteLimit,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DiscreteLimit.html.
Wolfram Research (2017),DiscreteLimit,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DiscreteLimit.html.CMS
Wolfram 语言. 2017. "DiscreteLimit." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteLimit.html.
Wolfram 语言. 2017. "DiscreteLimit." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteLimit.html.APA
Wolfram 语言. (2017). DiscreteLimit. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DiscreteLimit.html 年
Wolfram 语言. (2017). DiscreteLimit. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DiscreteLimit.html 年BibTeX
@misc{reference.wolfram_2025_discretelimit, author="Wolfram Research", title="{DiscreteLimit}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteLimit.html}", note=[Accessed: 02-April-2025
]}BibLaTeX
@online{reference.wolfram_2025_discretelimit, organization={Wolfram Research}, title={DiscreteLimit}, year={2017}, url={https://reference.wolfram.com/language/ref/DiscreteLimit.html}, note=[Accessed: 02-April-2025
]}