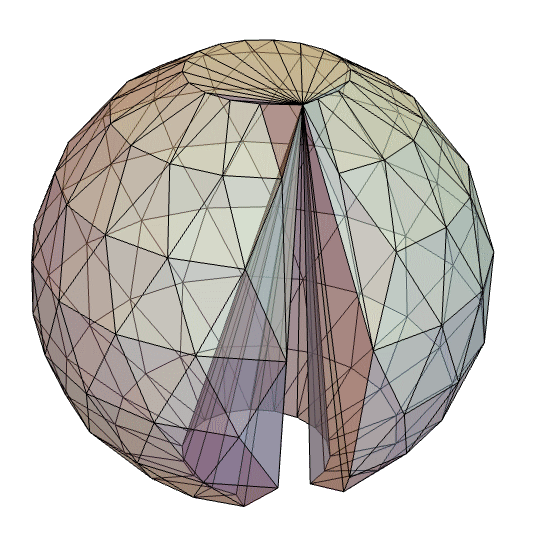OpenCascadeLink を使う
OpenCascadeLink を使う
このセクションでは，OpenCascadeLink が適用できる方法のいくつかについて説明する．OpenCascadeLink を使うには，まずロードする必要がある．
Needs["OpenCascadeLink`"]OpenCascadeの例の多くは，有限要素メッシュの機能と関係があるので，有限要素パッケージもロードする．
Needs["NDSolve`FEM`"]OpenCascade のプリミティブ
まず最初に OpenCascade オブジェクトを作成する必要がある．いくつかの方法でこれを行うことができる．3Dオブジェクトについては以下がある：
三次元立体プリミティブ
Wolfram言語のさまざまなGraphics3Dプリミティブを OpenCascade で表すことが可能である．これらのプリミティブは立体として表される．
Ball（球体）
2つの異なるBallプリミティブを OpenCascade で作成する．
shape1 = OpenCascadeShape[Ball[{1, 0, 0}]]
shape2 = OpenCascadeShape[Ball[{0, 1 / 2, 0}, 1 / 2]]OpenCascadeShapeType[shape1]境界付きのElementMeshを1つ目の OpenCascade の形状から生成する．
bmesh1 = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape1]境界付きのElementMeshを2つ目の OpenCascade の形状から生成する．
bmesh2 = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape2]境界付きのElementMeshを可視化する．
Show[bmesh1["Wireframe"], bmesh2["Wireframe"]]完全なElementMeshを生成する．
ToElementMesh[bmesh1]
ToElementMesh[bmesh2]いくつかのBallプリミティブを OpenCascade で生成する．
OpenCascadeShape[Ball[RandomReal[{-1, 1}, {4, 3}]]]CapsuleShape（カプセル形）
shape = OpenCascadeShape[CapsuleShape[{{0, -2, 0}, {0, 0, 1}}, 1]]OpenCascadeShapeType[shape]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]境界付きのElementMeshを可視化する．
bmesh["Wireframe"]完全にメッシュをかけられたElementMeshを可視化する．
ToElementMesh[bmesh]["Wireframe"]Cone（円錐）
Coneプリミティブを OpenCascade で作成する．
shape = OpenCascadeShape[Cone[{{0, 0, 0}, {0, 0, 1}}, 1]]OpenCascadeShapeType[shape]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]境界付きのElementMeshを可視化する．
bmesh["Wireframe"]完全にメッシュをかけられたElementMeshを可視化する．
ToElementMesh[bmesh]["Wireframe"]Cuboid（直方体）
Cuboidプリミティブを OpenCascade で作成する．
shape = OpenCascadeShape[Cuboid[{0, 0, 0}, {1, 2, 3}]]OpenCascadeShapeType[shape]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]境界付きのElementMeshを可視化する．
bmesh["Wireframe"]完全にメッシュをかけられたElementMeshを可視化する．
ToElementMesh[bmesh]["Wireframe"]Cylinder（円柱）
Cylinderプリミティブを OpenCascade で作成する．
shape = OpenCascadeShape[c1 = Cylinder[{{0, 0, 0}, {1, 2, 3}}, 1 / 2]]OpenCascadeShapeType[shape]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]境界付きのElementMeshとグラフィックスプリミティブを可視化する．
Show[bmesh["Wireframe"], Graphics3D[c1]]完全にメッシュをかけられたElementMeshを可視化する．
ToElementMesh[bmesh]["Wireframe"]Ellipsoid（楕円体）
Ellipsoidプリミティブを OpenCascade で作成する．
shape = OpenCascadeShape[el1 = Ellipsoid[{0, 0, 0}, {{5, 2, 3}, {2, 3, 2}, {3, 2, 5}}]]OpenCascadeShapeType[shape]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]境界付きのElementMeshとグラフィックスプリミティブを可視化する．
Show[bmesh["Wireframe"], Graphics3D[el1]]完全にメッシュをかけられたElementMeshを可視化する．
ToElementMesh[bmesh]["Wireframe"]FilledTorus（非空のトーラス）
FilledTorusプリミティブを OpenCascade で作成する．
shape = OpenCascadeShape[ft = FilledTorus[]]OpenCascadeShapeType[shape]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]境界付きのElementMeshとグラフィックスプリミティブを可視化する．
Show[bmesh["Wireframe"], Graphics3D[ft]]完全にメッシュをかけられたElementMeshを可視化する．
ToElementMesh[bmesh]["Wireframe"]Hexahedron（六面体）
Hexahedronプリミティブを OpenCascade で作成する．
shape = OpenCascadeShape[Hexahedron[{{0, 0, 0}, {1, 0, 0}, {2, 1, 0}, {1, 1, 0}, {0, 0, 1}, {1, 0, 1}, {2, 1, 1}, {1, 1, 1}}]]OpenCascadeShapeType[shape]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]境界付きのElementMeshを可視化する．
bmesh["Wireframe"]完全にメッシュをかけられたElementMeshを可視化する．
ToElementMesh[bmesh]["Wireframe"]Parallelepiped（平行六面体）
Parallelepipedプリミティブを OpenCascade で作成する．
p = Parallelepiped[{1, 0, 0}, {{1, 0, 0}, {1, 2, 1}, {0, 1, 1}}];
shape = OpenCascadeShape[p]OpenCascadeShapeType[shape]境界メッシュとParallelepipedを抽出して可視化する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape];
Show[
Graphics3D[{Opacity[0.25], p}],
bmesh["Wireframe"], Boxed -> False]Prism（角柱）
Prismプリミティブを OpenCascade で作成する．
shape = OpenCascadeShape[prism = Prism[{{1, 0, 1}, {0, 0, 0}, {2, 0, 0}, {1, 2, 1}, {0, 2, 0}, {2, 2, 0}}]]OpenCascadeShapeType[shape]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]境界付きのElementMeshとグラフィックスプリミティブを可視化する．
Show[bmesh["Wireframe"], Graphics3D[prism]]完全にメッシュをかけられたElementMeshを可視化する．
ToElementMesh[bmesh]["Wireframe"]Polyhedron（多面体）
Polyhedronプリミティブを OpenCascade で作成する．
polyhedron = Polyhedron[{{-Sqrt[1 + 2/Sqrt[5]], 0, Root[1 - 20*#1^2 + 80*#1^4 & , 3, 0]},
{Sqrt[1 + 2/Sqrt[5]], 0, Root[1 - 20*#1^2 + 80*#1^4 & , 2, 0]},
{Root[1 - 20*#1^2 + 80*#1^4 & , 1, 0], (-3 - Sqrt[5])/4, Root[1 - 20*#1^2 + 80*#1^4 & , 3, 0]},
{R ... },
{11, 12, 8, 16, 7}, {12, 6, 20, 4, 8}, {6, 2, 13, 18, 20}, {2, 5, 19, 17, 13},
{4, 20, 18, 10, 15}, {18, 13, 17, 9, 10}, {17, 19, 3, 14, 9}, {3, 7, 16, 1, 14},
{16, 8, 4, 15, 1}, {22, 23, 24}, {23, 22, 21}, {24, 21, 22}, {21, 24, 23}}];
shape = OpenCascadeShape[polyhedron]OpenCascadeShapeType[shape]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]境界付きのElementMeshを可視化する．
bmesh["Wireframe"]完全にメッシュをかけられたElementMeshを可視化する．
ToElementMesh[bmesh, "RegionHoles" -> {{0, 0, 0}}]["Wireframe"["MeshElement" -> "MeshElements", "MeshElementStyle" -> Directive[{FaceForm[Orange], EdgeForm[]}], PlotRange -> {{-1.5, 1.5}, {0, 1.5}, {-1.2, 1.2}}]]groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors, PlotRange -> {{-1.5, 1.5}, {0, 1.5}, {-1.2, 1.2}}]]Polyhedronプリミティブを OpenCascade で作成する．
r1 = TransformedRegion[Cuboid[], RotationTransform[Pi / 8, {1, 0, 0}]];
r2 = TransformedRegion[Cuboid[], RotationTransform[Pi / 8, {0, 1, 0}]];
polyhedron = RegionUnion[r1, r2];
shape = OpenCascadeShape[polyhedron]OpenCascadeShapeType[shape]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]境界付きのElementMeshを可視化する．
bmesh["Wireframe"]完全にメッシュをかけられたElementMeshを可視化する．
ToElementMesh[bmesh]["Wireframe"["MeshElement" -> "MeshElements", "MeshElementStyle" -> Directive[{FaceForm[Orange], EdgeForm[LightGray]}]]]Pyramid（錐体）
Pyramidプリミティブを OpenCascade で作成する．
shape = OpenCascadeShape[Pyramid[{{0, 0, 0}, {2, 0, 0}, {2, 2, 0}, {0, 2, 0}, {1, 1, 2}}]]OpenCascadeShapeType[shape]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]境界付きのElementMeshを可視化する．
bmesh["Wireframe"]完全にメッシュをかけられたElementMeshを可視化する．
ToElementMesh[bmesh]["Wireframe"]SphericalShell（球体殻）
SphericalShellプリミティブを OpenCascade で作成する．
shape = OpenCascadeShape[SphericalShell[]]OpenCascadeShapeType[shape]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]境界付きのElementMeshを可視化する．
bmesh["Wireframe"]領域の穴を残したまま，領域にメッシュをかける．完全にメッシュをかけられたElementMeshを可視化する．
ToElementMesh[bmesh, "RegionHoles" -> {{0, 0, 0}}]["Wireframe"]Tetrahedron（四面体）
Tetrahedronプリミティブを OpenCascade で作成する．
shape = OpenCascadeShape[Tetrahedron[{{0, 0, 0}, {1, 0, 0}, {0, 1, 0}, {0, 0, 2}}]]OpenCascadeShapeType[shape]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]境界付きのElementMeshを可視化する．
bmesh["Wireframe"]完全にメッシュをかけられたElementMeshを可視化する．
ToElementMesh[bmesh]["Wireframe"]拡張された三次元立体プリミティブ
OpenCascade は，Wolfram言語には直接対応するものがないプリミティブも提供する．
Torus（トーラス）
ここで引数は，トーラスが置かれている場所の周りの軸，その軸からトーラスの内部までの半径，トーラスの内側の半径を指定する2つ目の半径である．
shape = OpenCascadeShape[OpenCascadeTorus[{{0, 0, 0}, {0, 0, 1}}, 3, 1]]OpenCascadeShapeType[shape]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]境界付きのElementMeshを可視化する．
bmesh["Wireframe"]完全なElementMeshを生成する．
ToElementMesh[bmesh]shape = OpenCascadeShape[OpenCascadeTorus[{{0, 0, 0}, {0, 0, 1}}, 1, 0.1, π / 3]];
OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape, "ShapeSurfaceMeshOptions" -> {"AngularDeflection" -> 0.25}]["Wireframe"]曲面プリミティブ
3Dに埋め込まれた曲面グラフィックスプリミティブのインスタンスを作成することも可能である．
BSplineSurface（Bスプライン曲面）
pts = {{{0.5, 0, -0.5}, {0, 0, -0.5}, {0, 1, -0.5}, {0.5, 1, -0.5}, {1, 1, -0.5}, {1, 0, -0.5}, {0.5, 0, -0.5}},
{{0.5, 0, 0.7}, {0, 0, 0.7}, {0, 1, 0.7}, {0.5, 1, 0.7}, {1, 1, 0.7}, {1, 0, 0.7}, {0.5, 0, 0.7}},
{{0.5, 0, 0.9}, {0, 0, 0.9}, {0, 1, 1.5}, {0.5, 1, 1.5}, {1, 1, 1.5}, {1, 0, 0.9}, {0.5, 0, 0.9}},
{{0.5, -0.1, 1}, {0, -0.1, 1}, {0, 0.5, 2}, {0.5, 0.5, 2}, {1, 0.5, 2}, {1, -0.1, 1}, {0.5, -0.1, 1}},
{{0.5, -0.3, 1}, {0, -0.3, 1}, {0, -0.3, 2}, {0.5, -0.3, 2}, {1, -0.3, 2}, {1, -0.3, 1}, {0.5, -0.3, 1}},
{{0.5, -1.5, 1}, {0, -1.5, 1}, {0, -1.5, 2}, {0.5, -1.5, 2}, {1, -1.5, 2}, {1, -1.5, 1}, {0.5, -1.5, 1}}};w = {{1, .5, .5, 1, .5, .5, 1}, {1, .5, .5, 1, .5, .5, 1}, {1, .5, .5, 1, .5, .5, 1}, {1, .5, .5, 1, .5, .5, 1}, {1, .5, .5, 1, .5, .5, 1}, {1, .5, .5, 1, .5, .5, 1}};
uk = {0, 0, 0, 1 / 4, 1 / 2, 3 / 4, 1, 1, 1};
vk = {0, 0, 0, 1 / 4, 1 / 2, 1 / 2, 3 / 4, 1, 1, 1};
ud = 2;
vd = 2;
closed = {False, False};
bss = BSplineSurface[pts, SplineKnots -> {uk, vk}, SplineDegree -> {ud, vd},
SplineWeights -> w, SplineClosed -> closed];BSplineSurfaceプリミティブを OpenCascade で作成する．
surface = OpenCascadeShape[bss]OpenCascadeShapeType[surface]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[surface]Bスプライン曲面を持つ，境界付きのElementMeshを可視化する．
Show[bmesh["Wireframe"], Graphics3D[{Opacity[0.5], bss}]]完全にメッシュをかけられたElementMeshを非閉曲面から作成することはできない．
結び目と重みがAutomaticに設定されている，Bスプライン閉曲面はサポートされる．
pts = {
{{1, -1, 0}, {1, -1, 1}, {0, -1, 1}},
{{1, 0, 0}, {1, 0, 1}, {0, 0, 1}},
{{1, 1, 0}, {1, 1, 1}, {0, 0, 1}},
{{0, 1, 0}, {0, 1, 1}, {0, 0, 1}},
{{-1, 1, 0}, {-1, 1, 1}, {-1, 0, 1}}
};
uk = {0, 0, 0, 0, 1, 2, 2, 2, 2};
vk = {0, 0, 0, 1, 1, 1};
w = ConstantArray[1, Most[Dimensions[pts]]];
ud = 3;
vd = 2;
closed = {False, True};
bss = BSplineSurface[pts, SplineDegree -> {ud, vd},
SplineClosed -> closed];BSplineSurfaceプリミティブを OpenCascade で作成する．
surface = OpenCascadeShape[bss]OpenCascadeShapeType[surface]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[surface]Bスプライン曲面を持つ，境界付きのElementMeshを可視化する．
Show[bmesh["Wireframe"], Graphics3D[{Opacity[0.5], bss}]]3Dでの円板
OpenCascade は，Wolfram言語に直接対応していないプリミティブも提供する．
gr = Show[Graphics3D[Disk3D[{{0, 0, 1}, {0, -1, 0}}, 1 / 2, {π, 2π}]], Axes -> True, AxesLabel -> {"X", "Y", "Z"}]face = OpenCascadeShape[OpenCascadeDisk[{{0, 0, 1}, {0, -1, 0}}, 1 / 2, {π, 2π}]]OpenCascadeShapeType[face]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[face]境界付きのElementMeshを可視化する．
bmesh["Wireframe"]境界付きのElementMeshをグラフィックスとともに表示する．
Show[gr, bmesh["Wireframe"]]完全にメッシュを付けられたElementMeshを曲面から作成することはできない．
Polygon（多角形）
Polygonプリミティブを OpenCascade で作成する．
face = OpenCascadeShape[Polygon[{{0, 0, 0}, {1, 0, 0}, {1, 1, 0}, {0, 1, 0}}]]OpenCascadeShapeType[face]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[face]境界付きのElementMeshを可視化する．
bmesh["Wireframe"]完全にメッシュをかけられたElementMeshを曲面から作成することはできない．
穴が開いたPolygonを OpenCascade で作成する．
face = OpenCascadeShape[Polygon[{{0, 0, 0}, {3, 0, 0}, {3, 3, 0}, {0, 3, 0}, {1, 1, 0}, {1, 2, 0}, {2, 2, 0}, {2, 1, 0}}, {1, 2, 3, 4} -> {{5, 6, 7, 8}}]]OpenCascadeShapeType[face]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[face]境界付きのElementMeshを可視化する．
bmesh["Wireframe"]自己交差するPolygonを OpenCascade で指定する．
shape = OpenCascadeShape[Polygon[{{0.35, 0.2, 0}, {0.9, 0.75, 0}, {0.1, 0.55, 0}, {0.9, 0.35, 0}, {0.42, 0.9, 0}}]]OpenCascadeShapeType[shape]曲面メッシュを自己交差するPolygonから生成することはできない．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]Triangle（三角形）
Triangleプリミティブを OpenCascade で作成する．
face = OpenCascadeShape[Triangle[{{0, 0, 0}, {1, 0, 0}, {1, 1, 0}}]]OpenCascadeShapeType[face]境界付きのElementMeshを OpenCascade の形状から生成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[face]境界付きのElementMeshを可視化する．
bmesh["Wireframe"]完全にメッシュをかけられたElementMeshを非閉曲面から作成することはできない．
曲面メッシュ
ElementMesh（要素メッシュ）
ElementMeshは，Wolfram言語で有限要素解析に使われるメッシュ構造である．ElementMeshの作成については，ToBoundaryMeshおよびToElementMeshの関数ページ，または 「要素メッシュの生成」 のチュートリアルのドキュメントを参照されたい．
境界付きのElementMeshを作成して可視化する．
r = ImplicitRegion[-4 y^2 - 4 x y^2 + y^4 + 4 x z^2 + 4 x^2 z^2 + 2 y^2 z^2 + z^4 == 0, {x, y, z}];
bmesh = ToBoundaryMesh[r, {{-1, 1}, {-1, 1}, {-1, 1}}];
bmesh["Wireframe"]境界付きのElementMeshを OpenCascade オブジェクトに変換する．
shape = OpenCascadeShape[bmesh]それぞれの曲面要素が OpenCascade オブジェクトにマップされてから縫いつなげられるので，この変換は計算量的に高くつく．このようなタイプの形状の作成は，他に方法がない場合にのみ使用されるべきである．
OpenCascadeShapeType[shape]境界付きのElementMeshを作成して可視化する．
r = ImplicitRegion[x^6 - 5 x^4 y + 3 x^4 y^2 + 10 x^2 y^3 + 3 x^2 y^4 - y^5 + y^6 + z^2 ≤ 1, {x, y, z}];
bmesh = ToBoundaryMesh[r];
bmesh["Wireframe"]境界付きのElementMeshを OpenCascade オブジェクトに変換する．
shape = OpenCascadeShape[bmesh]OpenCascadeShapeType[shape]辺プリミティブ
3Dに埋め込まれた辺グラフィックスプリミティブのインスタンスを作成することも可能である．
Line（線）
wire = OpenCascadeShape[Line[{{0, 1, 0}, {1, 1, 0}, {1.5, 2, 0}, {2, 2, 0}}]]OpenCascadeShapeType[wire]境界付きのElementMeshをワイヤタイプの OpenCascade 形状から作成することはできない．しかし，ワイヤオブジェクトを回転スイープあるいは線形スイープに使うことや，他のワイヤや辺のオブジェクトと組み合せることはできる．
ワイヤを組み合せる
lines = {Line[{{0, 0, 0}, {1, 0, 0}}], Line[{{1, 0, 0}, {1, 1, 0}}], Line[{{1, 1, 0}, {0, 1, 0}}], Line[{{0, 1, 0}, {0, 0, 0}}]};Show[Graphics3D[lines], Axes -> True, AxesLabel -> {"X", "Y", "Z"}]wires = OpenCascadeShape /@ lineswire = OpenCascadeShapeWire[wires]OpenCascadeShapeType[wire]BezierCurve（ベジエ曲線）
BezierCurveを作成する．
bcurve = BezierCurve[{{1 / 50, 3 / 500, 0}, {2 / 500, 0, 0}, {1 / 50, -3 / 500, 0}}]BezierCurveを可視化する．
Graphics3D[bcurve, PlotRange -> {-0.001, 0.001}]BezierCurveプリミティブを OpenCascade で作成する．
edge = OpenCascadeShape[bcurve]OpenCascadeShapeType[edge]境界付きのElementMeshは，ワイヤタイプの OpenCascade 形状から作成することはできない．しかし，ワイヤオブジェクトを回転スイープあるいは線スイープに使うか，他のワイヤや辺のオブジェクトと組み合せることはできる．
w2 = OpenCascadeShape[Line[{{1 / 50, 3 / 500, 0}, {1 / 50, -3 / 500, 0}}]]face = OpenCascadeShapeFace[{edge, w2}]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[face]
bmesh["Wireframe"]BSplineCurve（Bスプライン曲線）
BSplineCurveを作成する．
pts = {{0, 0, 0}, {1, 1, 1}, {2, -1, 1}, {3, 0, 2}, {4, 1, 1}};
bsc = BSplineCurve[pts];BSplineCurveを可視化する．
Graphics3D[{bsc, Green, Line[pts], Red, Point[pts]}]edge = OpenCascadeShape[bsc]OpenCascadeShapeType[edge]境界付きのElementMeshは，ワイヤタイプの OpenCascade 形状から作成することはできない．しかし，ワイヤオブジェクトを回転スイープあるいは線スイープに使うか，他のワイヤや辺のオブジェクトと組み合せることはできる．
axis = {{0, 0, 0}, {1, 0, 0}};
gr = Graphics3D[{{Red, Thick, bsc}, {Blue, Arrow[axis]}}]BSplineCurveの回転スイープを作成する．
sweep = OpenCascadeShapeRotationalSweep[edge, axis, π / 2]Show[gr,
OpenCascadeShapeSurfaceMeshToBoundaryMesh[sweep]["Wireframe"]]拡張された辺プリミティブ
OpenCascade は，Wolfram言語に直接対応しないプリミティブも提供する．
三次元の円
Show[Graphics3D[Circle3D[{{0, 0, 1}, {0, -1, 0}}, 1 / 2, {π, 2π}]], Axes -> True, AxesLabel -> {"X", "Y", "Z"}]wire = OpenCascadeShape[OpenCascadeCircle[{{0, 0, 1}, {0, -1, 0}}, 1 / 2, {π, 2π}]]OpenCascadeShapeType[wire]境界付きのElementMeshをワイヤタイプの OpenCascade 形状から作成することはできない．しかし，ワイヤオブジェクトを回転スイープあるいは線形スイープに使うことや，他のワイヤや辺のオブジェクトと組み合せることはできる．
辺から曲面を作成する
ワイヤを使って曲面の境界を構築することも可能である．しかし，いくつかの制約がある．ワイヤは自己交差してはならない．ワイヤは閉じたループでなければならない．形成される曲面は平面でなければならない．
edges = {Line[{{0, 0, 0}, {1, 0, 0}}], OpenCascadeCircle[{{1, 1 / 2, 0}, {0, 0, 1}}, 1 / 2, {-π / 2, π / 2}], Line[{{1, 1, 0}, {0, 1, 0}}], Line[{{0, 1, 0}, {0, 0, 0}}]};Show[Graphics3D[edges /. OpenCascadeCircle -> Circle3D], Axes -> True, AxesLabel -> {"X", "Y", "Z"}]wires = OpenCascadeShape /@ edgeswire = OpenCascadeShapeWire[wires]surface = OpenCascadeShapeFace[wire]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[surface];
bmesh["Wireframe"]二次元立体プリミティブ
OpenCascade は，3DのCAD（コンピュータを使った設計システム）エンジンである．とは言っても，Disk，Rectangle等の2Dグラフィックスプリミティブを OpenCascade 形状に変換することも可能である．これを行うことには2つの理由が考えられる．
これがうまく行く基本的な方法は，2Dの埋込みオブジェクトを3Dの 
-
平面で作成し，
値を0と想定する．作成された形状は押出しのような3Dの OpenCascade 操作に埋め込まれるので，プール演算等がシステムの他の部分と同じように適用できる．
ワークフロー
最初のステップとして，両方の場合のワークフローを示す．まず半円板を作成することから始めよう．
i = OpenCascadeShape[Disk[{0, 0}, 1, {0, π}]]OpenCascadeShapeType[i]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[i]生成された境界付きのメッシュは3Dに埋め込まれ，
方向は0であることに注意する．このメッシュの3Dへの投影を下に示す．
Show[
OpenCascadeAxis3D[],
bmesh["Wireframe"]]先ほどの半円板オブジェクトに戻る．このオブジェクトは，変換関数を使うと他のどの位置にでも投影できる．これは他の OpenCascade 形状でも同じようにできる．
tf = RotationTransform[π / 2, {1, 0, 0}]i2 = OpenCascadeShapeTransformation[i, tf]Show[
OpenCascadeAxis3D[],
OpenCascadeShapeSurfaceMeshToBoundaryMesh[i2]["Wireframe"]]2Dの境界付きメッシュを作成するためには，関数ElementMeshProjectionが使える．
i = OpenCascadeShape[Disk[{0, 0}, 1, {0, π}]];
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[i];
ElementMeshProjection[bmesh, {#1, #2}&]["Wireframe"]境界付きメッシュの精緻化は標準的な方法で行える．この詳細については，曲面メッシュの生成のセクションに説明がある．
i = OpenCascadeShape[Disk[{0, 0}, 1, {0, π}]];
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[i, "ShapeSurfaceMeshOptions" -> {"AngularDeflection" -> 0.1}];
ElementMeshProjection[bmesh, {#1, #2}&]["Wireframe"]Annulus（環体）
2DのAnnulusを OpenCascade で作成する．
i = OpenCascadeShape[Annulus[{0, 0}, {1, 2}, {0, π}]]OpenCascadeShapeType[i]OpenCascadeShapeSurfaceMeshToBoundaryMesh[i]["Wireframe"]Disk（円板）
2DのDiskを OpenCascade で作成する．
i = OpenCascadeShape[Disk[{0, 0}, 1, {0, π}]]OpenCascadeShapeType[i]OpenCascadeShapeSurfaceMeshToBoundaryMesh[i]["Wireframe"]FilledCurve（非空の曲線）
FilledCurveは領域プリミティブではない．このグラフィックスの操作が部分的に OpenCascadeLink でサポートされている主な理由は，現行バージョンのMathematicaでは，2Dに埋め込まれている1Dの線分を繋げることによって2D領域を作成することができないからである．
curves = {BezierCurve[{{-1, 0}, {0, 1}, {1, 0}}], Line[{{1, 0}, {0, -2 / 3}, {-1, 0}}]};
Graphics[curves]グラフィックスでは，FilledCurveを使って曲線で囲まれた領域を指すことができる．
2DのFilledCurveを作成する．
fc = FilledCurve[curves];
Graphics[fc]2DのFilledCurveを OpenCascade で作成する．
i = OpenCascadeShape[fc]OpenCascadeShapeType[i]OpenCascadeShapeSurfaceMeshToBoundaryMesh[i]["Wireframe"]OpenCascadeLink がFilledCurveとJoinedCurveをサポートする方法は，Graphicsがこれらをサポートするのとは少し異なる．例えば，CircleはGraphicsでは線分として使えないが，OpenCascadeLink では使える．
fc = FilledCurve[{Line[{{-1, 0}, {1, 0}}], Circle[{0, 0}, 1, {0, π}]}]Graphics[fc /. Circle[data__] :> Sequence@@MeshPrimitives[DiscretizeRegion[Circle[data]], 1]]i = OpenCascadeShape[fc]OpenCascadeShapeType[i]OpenCascadeShapeSurfaceMeshToBoundaryMesh[i]["Wireframe"]OpenCascadeLink の実装では，FilledCurveとJoinedCurveに欠けている線分があってはならない．
fc = FilledCurve[{BezierCurve[{{-1, 0}, {0, 1}, {1, 0}}], Line[{{0, -2 / 3}, {-1, 0}}]}]i = OpenCascadeShape[fc]
JoinedCurveとFilledCurveのオプションは現在サポートされていない．
Parallelogram/Parallelepiped（平行四辺形／平行六面体）
2DのParallelogramを OpenCascade で作成する．
i = OpenCascadeShape[Parallelogram[]]OpenCascadeShapeType[i]OpenCascadeShapeSurfaceMeshToBoundaryMesh[i]["Wireframe"]Polygon（多角形）
2DのPolygonを OpenCascade で作成する．
i = OpenCascadeShape[Polygon[{{1, 0}, {0, Sqrt[3]}, {-1, 0}}]]OpenCascadeShapeType[i]OpenCascadeShapeSurfaceMeshToBoundaryMesh[i]["Wireframe"]Rectangle
2DのRectangleを OpenCascade で作成する．
i = OpenCascadeShape[Rectangle[]]OpenCascadeShapeType[i]OpenCascadeShapeSurfaceMeshToBoundaryMesh[i]["Wireframe"]RegularPolygon（正多角形）
2DのRegularPolygonを OpenCascade で作成する．
i = OpenCascadeShape[RegularPolygon[{1, 2}, {1 / 2, 0}, 6]]OpenCascadeShapeType[i]OpenCascadeShapeSurfaceMeshToBoundaryMesh[i]["Wireframe"]Triangle（三角形）
2DのTriangleを OpenCascade で作成する．
i = OpenCascadeShape[Triangle[{{1, 0}, {0, Sqrt[3]}, {-1, 0}}]]OpenCascadeShapeType[i]OpenCascadeShapeSurfaceMeshToBoundaryMesh[i]["Wireframe"]例
この例では，2Dのグラフィックスプリミティブを使って境界付きの要素メッシュを作成する方法について示す．ベジエ(Bezier)曲線で示される切取りがある複数材料の領域を作成する．
angle = 2π / 16;
r1 = 0.01;
r2 = 0.02;
offset = 1 / 1000;
faces = Disk[{0, 0}, #, {0, angle}]& /@ {r1, r1 + offset, r2};
cut = FilledCurve[{BezierCurve[{{1 / 50, 3 / 500}, {2 / 500, 0}, {1 / 50, -3 / 500}}], Line[{{1 / 50, -3 / 500}, {1 / 50, 3 / 500}}]}];Graphics[{Directive[FaceForm[], EdgeForm[Black]], faces, cut}, PlotRange -> {{0, r2}, All}]ofs = OpenCascadeShape /@ faces;
f1 = OpenCascadeShapeUnion[ofs]f2 = OpenCascadeShape[cut]f = OpenCascadeShapeDifference[f1, f2]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[f, "ShapeSurfaceMeshOptions" -> {"AngularDeflection" -> 0.1}];
bmesh["Wireframe"]mesh2D = ElementMeshProjection[bmesh, {#[[1]], #[[2]]}&]mesh2D["Wireframe"]bmesh2D = ToBoundaryMesh[mesh2D];
bmesh2D["Wireframe"](mesh = ToElementMesh[bmesh2D, "RegionMarker" -> {{{0.005, 0.001}, 1}, {{r1 + offset / 2, 0.00005}, 2, 0.0000001}, {{0.013, 0.004}, 3}}])["Wireframe"]境界付きの2Dプリミティブ
2D立体プリミティブのセクションで説明したように，2D立体グラフィックスプリミティブが変換できるのと同じように，LineやCircle等の2Dの辺や境界付きグラフィックスプリミティブも変換できる．
これがうまく行く基本的な方法は，2Dの埋込みオブジェクトを3Dの 
-
平面で作成し，
値を0と想定する．作成された形状は押出しのような3Dの OpenCascade 操作に埋め込まれるので，プール演算等がシステムの他の部分と同じように適用できる．
ワークフロー
最初のステップとして，両方の場合のワークフローを示す．まず半円と半円を閉じる線を作成することから始めよう．
i1 = OpenCascadeShape[Circle[{0, 0}, 1, {0, π}]]
i2 = OpenCascadeShape[Line[{{-1, 0}, {1, 0}}]]OpenCascadeShapeType /@ {i1, i2}次のステップは，ワイヤを繋げて，それらから面を作成することである．
wire = OpenCascadeShapeWire[{i1, i2}];
face = OpenCascadeShapeFace[wire]OpenCascadeShapeType[face]face = OpenCascadeShapeFace[{i1, i2}]OpenCascadeShapeType[face]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[face]生成された境界付きのメッシュは3Dに埋め込まれ，
方向は0であることに注意する．このメッシュの3Dへの投影を下に示す．
Show[
OpenCascadeAxis3D[],
bmesh["Wireframe"]]先ほどの半円と線のオブジェクトに戻る．このオブジェクトは，変換関数を使うと他のどの位置にでも投影できる．これは他の OpenCascade 形状でも同じようにできる．
tf = ReflectionTransform[{0, -1}, {0, 0}]i2 = OpenCascadeShapeTransformation[face, tf]Show[
OpenCascadeAxis3D[],
OpenCascadeShapeSurfaceMeshToBoundaryMesh[i2]["Wireframe"]]もとになる形状式は 
軸を0に設定し，3Dに埋め込まれているので，3D変換を適用することも可能である．
tf = RotationTransform[π / 2, {1, 0, 0}]i2 = OpenCascadeShapeTransformation[face, tf]Show[
OpenCascadeAxis3D[],
OpenCascadeShapeSurfaceMeshToBoundaryMesh[i2]["Wireframe"]]2Dの境界付きメッシュを作成するためには，関数ElementMeshProjectionが使える．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[face];
ElementMeshProjection[bmesh, {#[[1]], #[[2]]}&]["Wireframe"]境界付きメッシュの精緻化は標準的な方法で行える．この詳細については，曲面メッシュの生成のセクションに説明がある．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[face, "ShapeSurfaceMeshOptions" -> {"AngularDeflection" -> 0.1}];
ElementMeshProjection[bmesh, {#[[1]], #[[2]]}&]["Wireframe"]これで境界表現のでこぼこが少なくなった．境界のみを抽出するには，ToBoundaryMeshが適用できる．
ToBoundaryMesh[ElementMeshProjection[bmesh, {#[[1]], #[[2]]}&]]["Wireframe"]BezierCurve（ベジエ曲線）
BezierCurveを作成する．
bc = BezierCurve[{{1, 0}, {2, 1}, {3, 0}, {4, 1}}];
Graphics[bc]i = OpenCascadeShape[bc]OpenCascadeShapeType[i]BSplineCurve（Bスプライン曲線）
BSplineCurveを作成する．
bsc = BSplineCurve[{{1, 0}, {2, 1}, {3, 0}, {4, 1}}];
Graphics[bsc]i = OpenCascadeShape[bsc]OpenCascadeShapeType[i]Circle（円）
Circleを作成する．
c = Circle[{0, 0}, 1, {0, π}];
Graphics[c]i = OpenCascadeShape[c]OpenCascadeShapeType[i]JoinedCurve（結合曲線）
JoinedCurveは領域プリミティブではない．このグラフィックスの操作が部分的に OpenCascadeLink でサポートされている主な理由は，現行バージョンのMathematicaでは，2Dに埋め込まれている1Dの線分を繋げることによって2D領域を作成することができないからである．
curves = {BezierCurve[{{-1, 0}, {0, 1}, {1, 0}}], Line[{{1, 0}, {0, -2 / 3}, {-1, 0}}]};
Graphics[curves]グラフィックスでは，JoinedCurveを使って曲線で囲まれた領域を指すことができる．
JoinedCurveを作成する．
jc = JoinedCurve[curves];
Graphics[jc]JoinedCurveを OpenCascade で作成する．
i = OpenCascadeShape[jc]OpenCascadeShapeType[i]OpenCascadeLink がFilledCurveとJoinedCurveをサポートする方法は，Graphicsがこれらをサポートするのとは少し異なる．例えば，CircleはGraphicsでは線分として使えないが，OpenCascadeLink では使える．
jc = JoinedCurve[{Line[{{-1, 0}, {1, 0}}], Circle[{0, 0}, 1, {0, π}]}]Graphics[jc /. Circle[data__] :> Sequence@@MeshPrimitives[DiscretizeRegion[Circle[data]], 1]]i = OpenCascadeShape[jc]OpenCascadeShapeType[i]OpenCascadeLink の実装では，FilledCurveとJoinedCurveに欠けている線分があってはならない．
jc = JoinedCurve[{BezierCurve[{{-1, 0}, {0, 1}, {1, 0}}], Line[{{0, -2 / 3}, {-1, 0}}]}]OpenCascadeShape[jc]
JoinedCurveとFilledCurveのオプションは現在サポートされていない．
Line（線）
Lineを作成する．
l = Line[{{1, 0}, {2, 1}, {3, 0}, {4, 1}}];
Graphics[l]i = OpenCascadeShape[l]OpenCascadeShapeType[i]OpenCascade オブジェクトに対する操作
OpenCascade オブジェクトには以下の操作を施すことができる：
曲面メッシュの生成
OpenCascade オブジェクトの曲面にメッシュをかけることはできる．
shape = OpenCascadeShape[Cone[{{0, 0, 0}, {0, 0, 1}}, 1]]OpenCascadeShapeSurfaceMesh[shape]c = OpenCascadeShapeSurfaceMeshCoordinates[shape];
Graphics3D[Point[c]]ele = OpenCascadeShapeSurfaceMeshElements[shape];
Graphics3D[GraphicsComplex[c, Triangle[ele]]]Options[OpenCascadeShapeSurfaceMesh]"AngularDeflection"と"LinearDeflection"は，切片が真の局面から逸脱してもよい最大量を指定する．この概念は，以下の図で説明すると一番分かりやすい．
"AngularDeflection"が切片の端のノードにおける最大偏角 α を指定するのに対し，"LinearDeflection"は，切片内の真の曲線に対する最大偏向 
を指定する．"AngularDeflection"のAutomaticのデフォルトは，0.5度に，"LinearDeflection"のAutomaticのデフォルトは，形状の0.01単位の相対サイズに設定されている．この詳細については， OpenCascadeのドキュメントを参照されたい．
"ComputeInParallel"は，複数のCPUコア上で曲面の離散化が行われるべきかどうかを指定する．Automaticのデフォルトは Falseに設定されている．
"RelativeDeflection"は，偏向が形状の大きさに対して相対であるか，それとも絶対であるかを指定する．AutomaticのデフォルトはTrueに設定されている．
"Rediscretization"は，入力形状の一つがすでに離散化として形状に付けられていて，その離散化が再利用される場合に指定する．AutomaticのデフォルトはFalseに設定される．この機能は，複数のマテリアルを持つオブジェクト内のさまざまな部分にさまざまなレベルの離散化を持たせる場合に便利である．例は，縫合による内部境界の細分化のセクションにある．
OpenCascade と有限要素法を使うことを容易にするために，曲面にメッシュをかけ，境界付きのElementMeshを返す関数が提供されている．
境界付きのElementMeshを OpenCascade 形状から抽出する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]OpenCascade 形状から抽出した境界付きのElementMeshを可視化する．
bmesh["Wireframe"]bmesh["Wireframe"["MeshElementStyle" -> {FaceForm[Green], FaceForm[Red]}]]ToElementMesh[bmesh]["Wireframe"]Options[OpenCascadeShapeSurfaceMeshToBoundaryMesh]ElementMesh生成に関係のあるオプションはすべて"ElementMeshOptions"を通して，OpenCascadeShapeSurfaceMeshに関係のあるオプションは"ShapeSurfaceMeshOptions"を通して指定できる．
"MarkerMethod"オプションで，マーカーを追加するかどうかと，どのようにマーカーを計算すべきかを指定することができる．デフォルトは"OpenCascade"である．"ElementMesh"とNoneのオプションを使って，マーカーを完全にオフにすることもできる．"ElementMesh"を"MarkerMethod"オプションとして使うことは，生成された曲面が数多くの単一曲面からなる場合に役立つ．その場合，"OpenCascade"メソッドは，各要素に異なるマーカーを割り当てるので，これは望ましくないこともあるかも知れない．しかし，メソッド"ElementMesh"では，マーカーは面の法線に基づいて，法線がある一定量逸脱するかどうかによって，追加される．この詳細については，ToBoundaryMeshの関数ページを参照されたい．
洗練化された曲面メッシュを持つ OpenCascade の形状から境界付きのElementMeshを抽出する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape, "ShapeSurfaceMeshOptions" -> {"LinearDeflection" -> 0.001}]OpenCascade 形状から抽出した境界付きのElementMeshを可視化する．
bmesh["Wireframe"]部分の抽出
shape = OpenCascadeShape[Cone[]]OpenCascadeShapeNumberOfFaces[shape]faces = OpenCascadeShapeFaces[shape]OpenCascadeShapeType /@ facesOpenCascadeShapeSurfaceMeshToBoundaryMesh[faces[[1]]]["Wireframe"]OpenCascadeShapeNumberOfVertices[shape]vertices = OpenCascadeShapeVertices[shape]OpenCascadeShapeType /@ vertices幾何学的変換
shape = OpenCascadeShape[Cone[]]rshape = OpenCascadeShapeTransformation[shape, RotationTransform[10°, {0, 1, 0}]]境界付きのElementMeshを OpenCascade の形状から抽出する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[rshape]Wolfram言語で回転させた，境界付きのElementMeshと形状を可視化する．
Show[bmesh["Wireframe"], Graphics3D[TransformedRegion[Cone[], RotationTransform[10°, {0, 1, 0}]]]]もう一つの方法として，TransformedRegionを利用して，OpenCascade の形状の作成中にTransformationFunctionを直接適用することもできる．
rshape = OpenCascadeShape[TransformedRegion[Cone[], RotationTransform[20°, {0, 1, 1}]]]Wolfram言語で回転させた，境界付きのElementMeshと形状を抽出し，可視化する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[rshape];Show[bmesh["Wireframe"], Graphics3D[TransformedRegion[Cone[], RotationTransform[20°, {0, 1, 1}]]]]形状の鏡映を作るには，ReflectionTransformを使うとよい．
rt = ReflectionTransform[{0, 0, 1}, {0, 0, 1.1}];
rshape = OpenCascadeShape[TransformedRegion[Cone[], rt]]境界付きのElementMeshと鏡映された形状をWolfram言語で作成し，可視化する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[rshape];Show[bmesh["Wireframe"], Graphics3D[Cone[]]
, Graphics3D[GeometricTransformation[{Opacity[.85], Red, Cone[]}, rt]]
]スイープ
RotationalSweeps（回転スイープ）
OpenCascade は回転スイープを行うことができる．この場合，曲面を軸の周りで回転させる．回転は完全な一回転より小さくてもよい．
pp = Polygon[{{0, 0, 0}, {1, 0, 0}, {1, 1, 0}, {0, 1, 0}}];
shape = OpenCascadeShape[pp]OpenCascadeShapeType[shape]axis = {{2, 0, 0}, {2, 1, 0}};
sweep = OpenCascadeShapeRotationalSweep[shape, axis, -3π / 2]OpenCascadeShapeType[sweep]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[sweep];
Show[Graphics3D[{{Red, pp}, {Blue, Thick, Arrow[axis]}}], bmesh["Wireframe"], Boxed -> False]ToElementMesh[bmesh]OpenCascade は，ワイヤオブジェクトに対して回転スイープを行うこともできる．
ll = Line[{{0, 1, 0}, {1, 1, 0}, {1.5, 2, 0}, {2, 2, 0}}];
wire = OpenCascadeShape[ll]OpenCascadeShapeType[wire]axis = {{0, 0, 0}, {1, 0, 0}};
sweep = OpenCascadeShapeRotationalSweep[wire, axis]OpenCascadeShapeType[sweep]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[sweep];
Show[Graphics3D[{{Red, Thickness[0.02], ll}, {Blue, Thick, Arrow[axis]}}], bmesh["Wireframe"], Boxed -> False]回転スイープは，SolidあるいはCompoundSolidの OpenCascade 形状タイプには使えない．
OpenCascade は，辺オブジェクトにも回転スイープを行うことができる．
gr = {Red, Thickness[0.02], Circle3D[{{0, 0, 1}, {0, -1, 0}}, 1 / 2, {π, 2π}]};
Show[Graphics3D[gr], Axes -> True, AxesLabel -> {"X", "Y", "Z"}]wire = OpenCascadeShape[OpenCascadeCircle[{{0, 0, 1}, {0, -1, 0}}, 1 / 2, {π, 2π}]]OpenCascadeShapeType[wire]axis = {{0, 0, 0}, {1, 0, 0}};
sweep = OpenCascadeShapeRotationalSweep[wire, axis, 3π / 2]OpenCascadeShapeType[sweep]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[sweep];
Show[Graphics3D[{gr, {Blue, Thick, Arrow[axis]}}], bmesh["Wireframe"], Axes -> True, AxesLabel -> {"X", "Y", "Z"}]回転スイープは，SolidあるいはCompoundSolidの OpenCascade 形状タイプには使えない．
考えられる問題
回転スイープは，軸がスイープされる形状と交差し，その形状が交点で頂点も辺も持たない場合には行えない．以下の例を見てみよう．
line = Line[{{-1, 0, 0}, {1, 0, 0}}];
wire = OpenCascadeShape[line]axis = {{0, 0, -1}, {0, 0, 1}};
Graphics3D[{{Red, Thickness[0.02], line}, {Blue, Thick, Arrow[axis]}}, Axes -> True, AxesLabel -> {"X", "Y", "Z"}]sweep = OpenCascadeShapeRotationalSweep[wire, axis, π]この問題を修正する1つの方法は，回転が起るところに頂点または辺がある形状を作成することである．
line = Line[{{-1, 0, 0}, {0, 0, 0}, {1, 0, 0}}];
wire = OpenCascadeShape[line];
sweep = OpenCascadeShapeRotationalSweep[wire, axis, π]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[sweep];
bmesh["Wireframe"]より一般的な方法としては，例えばスプライン曲線の場合，半分の形状だけをモデル化し，2π についてスイープを行うことが可能である．
line = Line[{{0, 0, 0}, {1, 0, 0}}];
wire = OpenCascadeShape[line];
sweep = OpenCascadeShapeRotationalSweep[wire, axis, 2π];
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[sweep];
bmesh["Wireframe"]回転スイープは，SolidあるいはCompoundSolidの OpenCascade 形状タイプには使えない．
LinearSweeps（線形スイープ）
曲面の線形スイープには方向を与える必要がある．その後，曲面はその方向に沿ってスイープされる．
pp = Polygon[{{0, 0, 0}, {1, 0, 0}, {1, 1, 0}, {0, 1, 0}}];
shape = OpenCascadeShape[pp]OpenCascadeShapeType[shape]direction = {{1 / 2, 1 / 2, 0}, {1, 1, 1}};
sweep = OpenCascadeShapeLinearSweep[shape, direction]OpenCascadeShapeType[sweep]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[sweep];
Show[Graphics3D[{{Red, pp}, {Blue, Thick, Arrow[direction]}}], bmesh["Wireframe"], Boxed -> False]ToElementMesh[bmesh]OpenCascade は，ワイヤオブジェクトに対して線形スイープを行うこともできる．
ll = Line[{{0, 1, 0}, {1, 1, 0}, {1.5, 2, 0}, {2, 2, 0}}];
wire = OpenCascadeShape[ll]OpenCascadeShapeType[wire]axis = {{1 / 2, 1 / 2, 0}, {1, 1, 1}};
sweep = OpenCascadeShapeLinearSweep[wire, axis]OpenCascadeShapeType[sweep]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[sweep];
Show[Graphics3D[{{Red, Thickness[0.02], ll}, {Blue, Thick, Arrow[axis]}}], bmesh["Wireframe"], Boxed -> False]線形スイープは，SolidあるいはComSolidの OpenCascade 形状タイプには使えない．
経路に沿ったスイープ
面と経路が与えられると，OpenCascade はその面を経路に沿ってスイープすることができる．
bcurve = BezierCurve[{{0,0,0},{1,1/2,0},{0,1,0}}];
surface = Polygon[{{0,-l,-l},{0,l,-l},{0,l,l},{0,-l,l}}]/.l->1/8;Show[OpenCascadeAxis3D[], Graphics3D[{bcurve, surface}]]path = OpenCascadeShape[bcurve];
face = OpenCascadeShape[surface];経路は，タイプ"Edge"かタイプ"Wire"でなければならず，曲面には立体や複合体を含んではならない．
OpenCascadeShapeType /@ {face, path}pathSweep = OpenCascadeShapePathSweep[face, path]OpenCascadeShapeType[pathSweep]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[pathSweep]Show[
bmesh["Wireframe"], Graphics3D[{surface, {Thick, Red, bcurve}}]]ブール演算
ブール演算を行う際の制約については，ブール演算の問題のセクションと立体に対するブール演算のセクションに詳しい説明がある．
差
Ball形状を2個生成する．
b1 = Ball[];
b2 = Ball[{1, -1 / 2, 0}, 1 / 2];
shape1 = OpenCascadeShape[b1];
shape2 = OpenCascadeShape[b2];OpenCascadeShapeType /@ {shape1, shape2}difference = OpenCascadeShapeDifference[shape1, shape2]OpenCascadeShapeType[difference]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[difference];groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]ToElementMesh[bmesh]["Wireframe"]p1 = Prism[{{1, 0, 1}, {0, 0, 0}, {2, 0, 0}, {1, 2, 1}, {0, 2, 0}, {2, 2, 0}}];
b1 = Ball[{1, 0, -1 / 10}];Graphics3D[{p1, b1}]shape1 = OpenCascadeShape[p1];
shape2 = OpenCascadeShape[b1];difference = OpenCascadeShapeDifference[shape1, shape2]OpenCascadeShapeType[difference]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[difference];groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]ToElementMesh[bmesh]["Wireframe"]shape1 = OpenCascadeShape[SphericalShell[]];
shape2 = OpenCascadeShape[Cylinder[{{0, 0, 0}, {1, -2, 3}}, 1 / 2]];difference = OpenCascadeShapeDifference[shape1, shape2]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[difference];groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]ToElementMesh[bmesh]["Wireframe"]polyhedron = Polyhedron[{{-Sqrt[1 + 2/Sqrt[5]], 0, Root[1 - 20*#1^2 + 80*#1^4 & , 3, 0]},
{Sqrt[1 + 2/Sqrt[5]], 0, Root[1 - 20*#1^2 + 80*#1^4 & , 2, 0]},
{Root[1 - 20*#1^2 + 80*#1^4 & , 1, 0], (-3 - Sqrt[5])/4, Root[1 - 20*#1^2 + 80*#1^4 & , 3, 0]},
{R ... },
{11, 12, 8, 16, 7}, {12, 6, 20, 4, 8}, {6, 2, 13, 18, 20}, {2, 5, 19, 17, 13},
{4, 20, 18, 10, 15}, {18, 13, 17, 9, 10}, {17, 19, 3, 14, 9}, {3, 7, 16, 1, 14},
{16, 8, 4, 15, 1}, {22, 23, 24}, {23, 22, 21}, {24, 21, 22}, {21, 24, 23}}];
shape1 = OpenCascadeShape[polyhedron]
shape2 = OpenCascadeShape[Ball[{1, 0, 0}, 1 / 2]]difference = OpenCascadeShapeDifference[shape1, shape2]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[difference]groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調し，境界付きのElementMeshを通して，横断面を可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors, PlotRange -> {{-1.5, 1.5}, {0, 1.5}, {-1.2, 1.2}}]]ToElementMesh[bmesh]["Wireframe"]和
Ball形状を2個生成する．
b1 = Ball[];
b2 = Ball[{1, -1 / 2, 0}, 1 / 2];
shape1 = OpenCascadeShape[b1];
shape2 = OpenCascadeShape[b2];OpenCascadeShapeType /@ {shape1, shape2}union = OpenCascadeShapeUnion[shape1, shape2]OpenCascadeShapeType[union]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[union];groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]ToElementMesh[bmesh]["Wireframe"]shape1 = OpenCascadeShape[Ball[{0, 0, 1}, 1 / 2]];
shape2 = OpenCascadeShape[Hexahedron[{{0, 0, 0}, {1, 0, 0}, {2, 1, 0}, {1, 1, 0}, {0, 0, 1}, {1, 0, 1}, {2, 1, 1}, {1, 1, 1}}]];union = OpenCascadeShapeUnion[shape1, shape2]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[union];groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]ToElementMesh[bmesh]["Wireframe"]shape1 = OpenCascadeShape[Ball[{0, 0, 1}, 1 / 2]];
shape2 = OpenCascadeShape[Pyramid[{{0, 0, 0}, {2, 0, 0}, {2, 2, 0}, {0, 2, 0}, {1, 1, 2}} - 1]];union = OpenCascadeShapeUnion[shape1, shape2]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[union];groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]ToElementMesh[bmesh]["Wireframe"]shape1 = OpenCascadeShape[SphericalShell[]];
shape2 = OpenCascadeShape[Cylinder[{{0, 0, 0}, {1, 2, 3}}, 1 / 2]];OpenCascadeShapeType /@ {shape1, shape2}union = OpenCascadeShapeUnion[shape1, shape2]OpenCascadeShapeType[union]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[union];境界付きのElementMeshを可視化する．
bmesh["Wireframe"]ToElementMesh[bmesh]["Wireframe"]積
Ball形状を2個生成する．
b1 = Ball[];
b2 = Ball[{1, -1 / 2, 0}, 1 / 2];
shape1 = OpenCascadeShape[b1];
shape2 = OpenCascadeShape[b2];intersection = OpenCascadeShapeIntersection[shape1, shape2]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[intersection];groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]ToElementMesh[bmesh]["Wireframe"]shape1 = OpenCascadeShape[Ball[{0, 0, 1}, 1 / 2]];
shape2 = OpenCascadeShape[Hexahedron[{{0, 0, 0}, {1, 0, 0}, {2, 1, 0}, {1, 1, 0}, {0, 0, 1}, {1, 0, 1}, {2, 1, 1}, {1, 1, 1}}]];intersection = OpenCascadeShapeIntersection[shape1, shape2]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[intersection];groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]ToElementMesh[bmesh]["Wireframe"]shape1 = OpenCascadeShape[Ball[{0, 0, 1}, 1 / 2]];
shape2 = OpenCascadeShape[Pyramid[{{0, 0, 0}, {2, 0, 0}, {2, 2, 0}, {0, 2, 0}, {1, 1, 2}} - 1]];intersection = OpenCascadeShapeIntersection[shape1, shape2]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[intersection];groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]ToElementMesh[bmesh]["Wireframe"]shape1 = OpenCascadeShape[SphericalShell[]];
shape2 = OpenCascadeShape[Cylinder[{{0, 0, 0}, {1, 2, 3}}, 1 / 2]];OpenCascadeShapeType /@ {shape1, shape2}intersection = OpenCascadeShapeIntersection[shape1, shape2]OpenCascadeShapeType[intersection]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[intersection];境界付きのElementMeshを可視化する．
bmesh["Wireframe"]ToElementMesh[bmesh]["Wireframe"]積は，より低い次元の領域オブジェクトから生成することもできる．
c1 = Cone[{{0, 0, 0}, {0, 0, 1}}, 1];
shape1 = OpenCascadeShape[c1];
shape2 = OpenCascadeShape[Polygon[{{-2, 0, -2}, {2, 0, -2}, {2, 0, 2}, {-2, 0, 2}}]];OpenCascadeShapeType /@ {shape1, shape2}intersection = OpenCascadeShapeIntersection[shape1, shape2]OpenCascadeShapeType[intersection]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[intersection];境界付きのElementMeshを可視化する．
bmesh["Wireframe"]Show[bmesh["Wireframe"["MeshElementStyle" -> Directive[FaceForm[Green], EdgeForm[Red]]]], Graphics3D[{Opacity[0.15], c1}], Boxed -> False]ブール演算の簡略化
c1 = Cuboid[{0, 0, 0}, {1, 1, 1}];
c2 = Cuboid[{1 / 2, 0, 0}, {2, 2, 2}];
u1 = OpenCascadeShapeUnion[OpenCascadeShape /@ {c1, c2}];
OpenCascadeShapeSurfaceMeshToBoundaryMesh[u1]["Wireframe"]c1 = Cuboid[{0, 0, 0}, {1, 1, 1}];
c2 = Cuboid[{1 / 2, 0, 0}, {2, 2, 2}];
u1 = OpenCascadeShapeUnion[OpenCascadeShape /@ {c1, c2}, "SimplifyResult" -> True];
OpenCascadeShapeSurfaceMeshToBoundaryMesh[u1]["Wireframe"]BooleanRegion（ブール領域）
OpenCascadeLink は，直接BooleanRegionオブジェクトを使うことができる機能を提供する．
BooleanRegion形状を生成する．
shape = OpenCascadeShapeBooleanRegion[BooleanRegion[Or, {Cuboid[], Ball[{1, 1, 1}]}]]便利なことに，OpenCascadeShapeをBooleanRegionオブジェクトに使うことも可能である．
BooleanRegion形状を生成する別の方法．
shape = OpenCascadeShape[BooleanRegion[Or, {Cuboid[], Ball[{1, 1, 1}]}]]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape];groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]ToElementMesh[bmesh]["Wireframe"]BooleanRegion形状を生成する．
shape = OpenCascadeShape[BooleanRegion[And, {Cuboid[], Ball[{1, 1, 1}]}]]OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Wireframe"]BooleanRegion形状を生成する．
shape = OpenCascadeShape[BooleanRegion[¬#2∧#1&, {Cuboid[], Ball[{1, 1, 1}]}]]OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Wireframe"]立体に対するブール演算
OpenCascade は，Wolfram言語のブール演算子であるRegionUnion，RegionIntersection，RegionDifferenceとは少し異なる形でブール演算を処理する．いくつかの例題を通して見てみよう．
立体の重なり
gr1 = Graphics3D[{{Opacity[0.5], c1 = Cuboid[], c2 = Cuboid[{1 / 4, 1 / 4, 1 / 4}]}}, Boxed -> False]s1=OpenCascadeShape[c1];
s2=OpenCascadeShape[c2];shape = OpenCascadeShapeIntersection[s1, s2];Show[gr1, OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Wireframe"["MeshElementStyle" -> {FaceForm[Blue]}]]]shape = OpenCascadeShapeUnion[s1, s2];Show[gr1, OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Wireframe"["MeshElementStyle" -> {FaceForm[Blue]}]]]shape = OpenCascadeShapeDifference[s1, s2];Show[gr1, OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Wireframe"["MeshElementStyle" -> {FaceForm[Blue]}]]]shape = OpenCascadeShapeDifference[s2, s1];Show[gr1, OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Wireframe"["MeshElementStyle" -> {FaceForm[Blue]}]]]面が触れ合っている立体
gr1 = Graphics3D[{{Opacity[0.5], c1 = Cuboid[], c2 = Cuboid[{1, 1 / 2, 1 / 2}]}}, Boxed -> False]s1=OpenCascadeShape[c1];
s2=OpenCascadeShape[c2];shape = OpenCascadeShapeIntersection[s1, s2];OpenCascase のブール演算から得ることができる最低次元のオブジェクトは，ブール演算に与えられた任意引数の最低次元のオブジェクトである．例えば，2つの OpenCascade の立体のブール演算が OpenCascade の面オブジェクトを返すことはできない．
OpenCascadeShapeNumberOfFaces[shape]OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]shape = OpenCascadeShapeUnion[s1, s2];Show[gr1, OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Wireframe"["MeshElementStyle" -> {FaceForm[Blue]}]]]ToElementMesh[OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape], MaxCellMeasure -> 0.005]["Wireframe"]shape = OpenCascadeShapeDifference[s1, s2];Show[gr1, OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Wireframe"["MeshElementStyle" -> {FaceForm[Blue]}]]]結果の立体は，触れ合っているオブジェクトの形状に従って，その表面が分割されている．
OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Wireframe"["MeshElementStyle" -> {FaceForm[Blue]}]]shape = OpenCascadeShapeDifference[s2, s1];Show[gr1, OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Wireframe"["MeshElementStyle" -> {FaceForm[Blue]}]]]結果の立体は，触れ合っているオブジェクトの形状に従って，その表面が分割されている．
辺の部分で接触している立体
gr1 = Graphics3D[{{Opacity[0.5], c1 = Cuboid[], c2 = Cuboid[{1, 1, 1 / 2}]}}, Boxed -> False]s1=OpenCascadeShape[c1];
s2=OpenCascadeShape[c2];shape = OpenCascadeShapeIntersection[s1, s2];OpenCascase のブール演算から得ることができる最低次元のオブジェクトは，ブール演算に与えられた任意引数の最低次元のオブジェクトである．例えば，2つの OpenCascade の立体のブール演算が OpenCascade の面オブジェクトを返すことはできない．
OpenCascadeShapeNumberOfEdges[shape]shape = OpenCascadeShapeUnion[s1, s2];Show[gr1, OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Wireframe"["MeshElementStyle" -> {FaceForm[Blue]}]]]結果の完全なメッシュの辺は，触れ合っている辺で分割されている．
ToElementMesh[OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape], MaxCellMeasure -> Infinity]["Wireframe"]shape = OpenCascadeShapeDifference[s1, s2];Show[gr1, OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Wireframe"["MeshElementStyle" -> {FaceForm[Blue]}]]]結果の境界メッシュの辺は，触れ合っている辺で分割されている．
OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Wireframe"["MeshElementStyle" -> {FaceForm[Blue]}]]shape = OpenCascadeShapeDifference[s2, s1];Show[gr1, OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Wireframe"["MeshElementStyle" -> {FaceForm[Blue]}]]]結果の境界メッシュの辺は，触れ合っている辺で分割されている．
形状の分割
立体等の形状がある場合に，そのオブジェクトを複数の部分に分割したいことがある．立体は別の立体あるいは面で分割できる．分割される形状はオブジェクトと呼ばれ，分割を行う形状はツールと呼ばれる．
r = RegionDifference[Cuboid[{0, 0, 0}, {1, 1, 1}], Cuboid[{0.1, 0.1, 0.1}, {0.9, 0.9, 0.9}]];
shape = OpenCascadeShape[r];t = Cuboid[{0.5, 0.5, 0.5}, {1.5, 1.5, 1.5}];
tool = OpenCascadeShape[t]OpenCascadeShapeType[shape]OpenCascadeShapeType[tool]Show[
Region[Style[r, Opacity[0.2]]], Graphics3D[{Opacity[0.2], LightRed, t}], OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Edgeframe"], OpenCascadeShapeSurfaceMeshToBoundaryMesh[tool]["Edgeframe"]]split = OpenCascadeShapeSplit[shape, tool]bmeshes = OpenCascadeShapeSurfaceMeshToBoundaryMesh /@ split#["Wireframe"]& /@ bmeshesShow[
Region[Style[r, Opacity[0.2]]], Graphics3D[{Opacity[0.2], LightRed, t}], #["Edgeframe"]]& /@ bmeshesToElementMesh[OpenCascadeShapeSurfaceMeshToBoundaryMesh[#]]["Wireframe"]& /@ splitt = Polygon[{{-1, -1, 1 / 2}, {2, -1, 1 / 2}, {2, 2, 1 / 2}, {-1, 2, 1 / 2}}];
tool = OpenCascadeShape[t]OpenCascadeShapeType[tool]Show[
Region[Style[r, Opacity[0.2]]], Graphics3D[t], OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Edgeframe"]]split = OpenCascadeShapeSplit[shape, tool]OpenCascadeShapeSurfaceMeshToBoundaryMesh[#]["Wireframe"]& /@ split立体はワイヤでは分割できない．面は別の面かワイヤで分割できる．
r = Polygon[{{0, 0, 1 / 2}, {1, 0, 1 / 2}, {1, 1, 1 / 2}, {0, 1, 1 / 2}}];
shape = OpenCascadeShape[r]t = Line[{{-1, 0, 1 / 2}, {1 / 2, 1 / 2, 1 / 2}, {2, 0, 1 / 2}}];
tool = OpenCascadeShape[t]OpenCascadeShapeType[tool]Graphics3D[{r, t}]split = OpenCascadeShapeSplit[shape, tool]OpenCascadeShapeSurfaceMeshToBoundaryMesh[#]["Wireframe"]& /@ splitツールは正しい形状タイプであることが重要である．"Edge"タイプの形状ツールが与えられると，自動的に"Wire"ツールに変換される．
縫合
辺を共有する曲面は縫い合わせることができる．より正確には，縫合とは位相的に不連続である面を縫い合せて殻にすることである．
data = {Polygon[{{0, 1, 0}, {1, 0, 0}, {0, 0, 0}}], Polygon[{{0, 0, 2}, {1, 0, 0}, {0, 0, 0}}], Polygon[{{0, 0, 2}, {0, 1, 0}, {1, 0, 0}}], Polygon[{{0, 0, 2}, {0, 0, 0}, {0, 1, 0}}]};ocFaces = OpenCascadeShape[#]& /@ dataOpenCascadeShapeType /@ ocFacessewenFaces = OpenCascadeShapeSewing[ocFaces]OpenCascadeShapeType[sewenFaces]殻は，面の集合である．立体を作成するためには，縫合の過程でオプションを使うか，関数OpenCascadeShapeSolidを使うかすればよい．
sewenFaces = OpenCascadeShapeSewing[ocFaces, "BuildSolid" -> True]OpenCascadeShapeType[sewenFaces]境界付きのElementMeshを抽出して可視化する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[sewenFaces]
bmesh["Wireframe"]ToElementMesh[bmesh]["Wireframe"]Bスプライン曲面を他のオブジェクトと縫い合わせることは可能である．ただし，ノードが合致しなければならない．
PolarPlotを作成する．
pp = PolarPlot[1 + 0.5 Sin[2 θ], {θ, 0, 2 π}, MaxRecursion -> 1, PlotPoints -> 45]PolarPlotから座標を抽出する．
coordinates = First[Cases[Normal[pp], Line[l_] :> l, ∞]];parametrizeCurve[pts_List, a : (_ ? NumericQ) : 1 / 2] := FoldList[Plus, 0, Normalize[(Norm /@ Differences[pts]) ^ a, Total]] /; MatrixQ[pts, NumericQ]
tvals = parametrizeCurve[coordinates, 1];BSplineSurfaceを構築する．
bottom = ArrayPad[coordinates,{{0,0},{0,1}},-1.];
top = ArrayPad[coordinates,{{0,0},{0,1}},2.];
knots = Join[{0.,0.},tvals[[2;;-2]],{1.,1.}];
bss = BSplineSurface[Transpose[{bottom,top}],SplineDegree->1,SplineKnots->{knots,{0,0,1,1}}];BSplineSurfaceと上下のキャップを可視化する．
gr = Graphics3D[{EdgeForm[], Polygon[top], Polygon[bottom], bss}, Boxed -> False]surface = OpenCascadeShape[bss];
p1 = OpenCascadeShape[Polygon[top]];
p2 = OpenCascadeShape[Polygon[bottom]];shape = OpenCascadeShapeSewing[{surface, p1, p2}]OpenCascadeShapeType[shape]shape = OpenCascadeShapeSolid[shape];
OpenCascadeShapeType[shape]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape];
Show[gr, bmesh["Wireframe"], Boxed -> False]ToElementMesh[bmesh]もう一つの例として，8個のBSplineSurfaceパッチからEllipsoidを作成する．
Ellipsoidを作成して可視化する．
center = {0, 1, -1 / 2};
sigma = {{5, 2, 3}, {2, 3, 2}, {3, 2, 5}};
el = Ellipsoid[center, sigma];
gr = Graphics3D[el, Boxed -> False]Ellipsoidの固有値と固有ベクトルを計算する．
matrix = If[VectorQ[sigma],
DiagonalMatrix[sigma ^ 2],
sigma];
{vals, vecs} = Eigensystem[N[matrix]];composition = Composition[TranslationTransform[center], AffineTransform[Transpose[vecs]], ScalingTransform[Sqrt[vals]]]pts1 = {{{1, 0, 0}, {1, 1, 0}, {0, 1, 0}},
{{1, 0, 1}, {1, 1, 1}, {0, 1, 1}},
{{0, 0, 1}, {0, 0, 1}, {0, 0, 1}}};
pts2 = {{{0, 1, 0}, {-1, 1, 0}, {-1, 0, 0}},
{{0, 1, 1}, {-1, 1, 1}, {-1, 0, 1}},
{{0, 0, 1}, {0, 0, 1}, {0, 0, 1}}};
pts3 = {{{-1, 0, 0}, {-1, -1, 0}, {0, -1, 0}},
{{-1, 0, 1}, {-1, -1, 1}, {0, -1, 1}},
{{0, 0, 1}, {0, 0, 1}, {0, 0, 1}}};
pts4 = {{{0, -1, 0}, {1, -1, 0}, {1, 0, 0}},
{{0, -1, 1}, {1, -1, 1}, {1, 0, 1}},
{{0, 0, 1}, {0, 0, 1}, {0, 0, 1}}};
pts = {pts1, pts2, pts3, pts4, -pts1, -pts2, -pts3, -pts4};
bsss = Table[BSplineSurface[composition /@ d, SplineDegree -> 2, SplineKnots -> {{0, 0, 0, 1, 1, 1}, {0, 0, 0, 1, 1, 1}}, SplineWeights -> {{1, 1 / Sqrt[2], 1}, {1 / Sqrt[2], 1 / 2, 1 / Sqrt[2]}, {1, 1 / Sqrt[2], 1}}], {d, pts}];
bsurfs = OpenCascadeShape /@ bsssshape = OpenCascadeShapeSewing[bsurfs, "BuildSolid" -> True]OpenCascadeShapeType[shape]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape];
Show[gr, bmesh["Wireframe"], Boxed -> False]可能な問題として，縫合に与えられる曲面の順序に対して OpenCascade が敏感であるということが挙げられる．表示された曲面が問題なく見えても，例えばブーリアン演算をオブジェクトに対して行ったときに予期しない結果が起る可能性があるので，この問題には注意が必要である．
cu = OpenCascadeShape[Cuboid[{0, 0, 0}, {2, 2, 2}]];
union = OpenCascadeShapeUnion[cu, shape];
OpenCascadeShapeSurfaceMeshToBoundaryMesh[union]["Wireframe"]内部境界
OpenCascade には，内部境界を含む方法がいくつかある．
面の和による内部境界
立体の和を形成すると，重なり合っている位置が開いた状態になる．
Graphics3D[{{Opacity[0.5], c1 = Cuboid[{0, 0, 0}, {0.5, 1, 1}], c2 = Cuboid[{0.5, 0, 0}, {1, 1, 2}]}}, Boxed -> False]shape1 = OpenCascadeShape[c1];
shape2 = OpenCascadeShape[c2];union = OpenCascadeShapeUnion [shape1, shape2];
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[union];
ToElementMesh[bmesh, MaxCellMeasure -> 0.01]["Wireframe"]2つの直方体が触れ合っている部分では，和は閉じないことに注意する．複数のマテリアル領域を扱っている場合にはこのことは望ましくないかもしれない．重なり合った部分で面を閉じる1つのオプションは，立体の面すべての和を計算することである．
faces1 = OpenCascadeShapeFaces[shape1];
faces2 = OpenCascadeShapeFaces[shape2];
union = OpenCascadeShapeUnion[Flatten[{faces1, faces2}]]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[union];
ToElementMesh[bmesh, MaxCellMeasure -> 0.01]["Wireframe"]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[union];
ToElementMesh[bmesh]["Wireframe"]これで，2つの立体の間に面が存在するようになったことに注意する．
縫合による内部境界
形状の縫合を使って，内部に境界を持つ形状を生成することもできる．
shape1 = OpenCascadeShape[Cuboid[{-2, -2, -2}, {2, 2, 1 / 2}]];
shape2 = OpenCascadeShape[Cylinder[]];union = OpenCascadeShapeUnion [shape1, shape2]OpenCascadeShapeSurfaceMeshToBoundaryMesh[union]["Wireframe"]intersection = OpenCascadeShapeIntersection [shape1, shape2]OpenCascadeShapeSurfaceMeshToBoundaryMesh[intersection]["Wireframe"]shape = OpenCascadeShapeSewing[{union, intersection}]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape];groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors, PlotRange -> {All, {-1, 2}, All}]]2つの形状の積は閉じているので，その閉形状を形状の和に縫い合わせることによって，3つの内部領域が生成される．直方体の上の円柱，直方体内部にある円柱，そして残りの直方体の3つである．
mesh = ToElementMesh[bmesh, "RegionMarker" -> {{{-1, -1, -1}, 1}, {{0, 0, 3 / 4}, 2}, {{0, 0, 1 / 4}, 3}}]mesh["MeshElementMarkerUnion"]parts = Map[mesh["Wireframe"[ElementMarker == #[[1]], "MeshElement" -> "MeshElements", "ElementMeshDirective" -> Directive[EdgeForm[], FaceForm[#[[2]]]]]]&, {{1, Gray}, {2, Pink}, {3, Orange}}]Rasterize[Show[parts, PlotRange -> {All, {-0.02, 2}, All}]]縫合による内部境界の細分化
複数の内部境界をさまざまな解像度で離散化することが望ましい場合もある．これは，それぞれの境界を希望するレベルで離散化し，それを縫い合せることによって可能である．
cylinder = Cylinder[{{0, 0, 3.097}, {0, 0, 3.097 + 6}}, 3];
cuboid1 = Cuboid[{-10, -10, -10}, {10, 10, 10}];
cuboid2 = Cuboid[{-5, -5, -2}, {5, 5, 2}];cylinderShape = OpenCascadeShape[cylinder];
cuboid1Shape = OpenCascadeShape[cuboid1];
cuboid2Shape = OpenCascadeShape[cuboid2];
shape = OpenCascadeShapeSewing[{cylinderShape, cuboid1Shape, cuboid1Shape}]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape];
bmesh["Wireframe"]内部の円柱を細分化したいが，直方体の境界はしたくないという場合はどうだろうか．オブジェクトを縫い合せる最中に，線形偏向あるいは角偏向を変更すると，すべての境界が影響を受ける．それでもオブジェクト内の単一の形状の離散化を変更したい場合には，そのオブジェクトの曲面メッシュを施し，縫合の際にその離散化を保持することが可能である．
OpenCascadeShapeSurfaceMesh[cylinderShape, "LinearDeflection" -> 0.00125]離散化はOpenCascadeShapeExpressionに施されていることに注意する．
shape = OpenCascadeShapeSewing[{cylinderShape, cuboid1Shape, cuboid2Shape}]OpenCascadeShapeExpressionに施された境界の離散化を利用するためには，OpenCascadeShapeSurfaceMeshToBoundaryMeshにオプション"Rediscretization"Falseを使って，あれば前の離散化を利用する必要がある．
形状にすでに境界離散化が施されている場合には，再度離散化せずに境界ElementMeshを作成する．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape, "ShapeSurfaceMeshOptions" -> {"Rediscretization" -> False}];
bmesh["Wireframe"]今度は，内部円柱が残りの境界とは異なるレベルで離散化された．
フィレット
OpenCascade は，形状にフィレットを付ける機能を提供する．
shape = OpenCascadeShape[Cuboid[{0, 0, 0}, {1, 2, 3}]]OpenCascadeShapeType[shape]fillet = OpenCascadeShapeFillet[shape, 0.25]OpenCascadeShapeType[fillet]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[fillet]groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]ToElementMesh[bmesh]["Wireframe"]shape = OpenCascadeShape[Cuboid[{0, 0, 0}, {1, 2, 3}]]OpenCascadeShapeNumberOfEdges[shape]OpenCascade では，それぞれの面がその面を囲む辺すべてにアクセスできる．立方体の場合，それぞれの面は4つの辺に接続している．面は6つあるので，全部で24本の辺に操作を行うことが可能で，そのうち12本の辺が重複している．
fillet = OpenCascadeShapeFillet[shape, 0.25, {1, 7}]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[fillet]groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]すべての辺について全体の形状にフィレットが与える影響を見ると便利なこともあれば，フィレットを付けたい辺を見極める必要があることもある．そのために使えるVisualizeEdgeFunctionというヘルパ関数があり，これは，索引で定義されている．
VisualizeEdgeFunction[Cuboid[{0, 0, 0}, {1, 2, 3}], OpenCascadeShapeFillet[#1, 0.25, #2]&]face = OpenCascadeShape[Polygon[{{0, 0, 0}, {1, 0, 0}, {1, 1, 0}, {0, 1, 0}}]];
sweep = OpenCascadeShapeRotationalSweep[face, {{2, 0, 0}, {2, 1, 0}}, -3π / 2];
shape1 = OpenCascadeShape[Cylinder[{{1, -1, 0}, {1, 1, 0}}, 1 / 2]];
shape = OpenCascadeShapeUnion[sweep, shape1]fillet = OpenCascadeShapeFillet[shape, 0.125]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[fillet]境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> Directive[FaceForm[LightBlue], EdgeForm[]]]]要求されたフィレットの半径が大きすぎる場合にはフィレットを付けることに失敗する．
shape = OpenCascadeShape[Cylinder[{{1, -1, 0}, {1, 1, 0}}, 1 / 2]]fillet = OpenCascadeShapeFillet[shape, 1]fillet = OpenCascadeShapeFillet[shape, 0.025]OpenCascadeShapeSurfaceMeshToBoundaryMesh[fillet]["Wireframe"]C面取り
C面取りはフィレットに似ている．違いは，C面取りでは角は丸められず，平面である点である．作成されたC面取りは対称であり，関数のパラメータは，作成されるC面取りの曲面に接線方向である距離を指定する．
shape = OpenCascadeShape[Cuboid[{0, 0, 0}, {1, 2, 3}]]OpenCascadeShapeType[shape]chamfer = OpenCascadeShapeChamfer[shape, 0.25, {5, 6}]OpenCascadeShapeType[chamfer]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[chamfer]groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]ToElementMesh[bmesh]すべての辺について全体の形状にC面取りが与える影響を見ると便利なこともあれば，C面取りを施したい辺を見極める必要があることもある．そのために使えるVisualizeEdgeFunctionというヘルパ関数があり，これは，索引で定義されている．
VisualizeEdgeFunction[Cuboid[{0, 0, 0}, {1, 2, 3}], OpenCascadeShapeChamfer[#1, 0.25, #2]&]ロフト
ロフトとは，ワイヤを通過する曲面を作成することによって生成される曲面あるいは立体である．この概念は，可視化を使った説明で理解しやすい．
w1 = Line[{{0, 0, 0}, {1, 0, 0}, {0, 1, 0}, {0, 0, 0}}];
w2 = OpenCascadeCircle[{{1 / 2, 1 / 2, 1}, {0, 0, 1}}, 1 / 4];
w3 = Line[{{0, 0, 2}, {0.7, 0, 2}, {0, 0.7, 2}, {0, 0, 2}}];
gr = Graphics3D[{Red, Thickness[0.02], {w1, w2, w3}} /. OpenCascadeCircle -> Circle3D, Boxed -> False]Loftコマンドは，与えられたオブジェクトを通過する曲面を作成することで曲面または立体を生成する．
s = OpenCascadeShape /@ {w1, w2, w3}ロフトは，"Wire"あるいは"Face"の形状オブジェクトから生成できる．ただし，オブジェクトはすべて同じタイプでなければならない．
OpenCascadeShapeType /@ sloft = OpenCascadeShapeLoft[s]Show[
gr,
OpenCascadeShapeSurfaceMeshToBoundaryMesh[loft]["Wireframe"]
]デフォルトで，ワイヤオブジェクトから作成されたロフトは，開いた殻を返す．
OpenCascadeShapeType[loft]完全メッシュの生成に適切な立体を生成するためには，オプションを"BuildSolid"Trueに設定する．
loft = OpenCascadeShapeLoft[s, "BuildSolid" -> True];
OpenCascadeShapeType[loft]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[loft];
mesh = ToElementMesh[bmesh, MaxCellMeasure -> Infinity]Show[gr,
mesh["Wireframe"["MeshElementStyle" -> FaceForm[Orange]]]]f[t_] := {1 / 2 * Cos[10 * t], 1 / 2 * Sin[10 * t], t / 4};
circles = Table[OpenCascadeCircle[{f[t], f'[t]}, 1 / 20], {t, 0, 2 π, 2 π / 61}];
s = OpenCascadeShape /@ circles;
loft = OpenCascadeShapeLoft[s, "BuildSolid" -> True];
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[loft, "ShapeSurfaceMeshOptions" -> {"AngularDeflection" -> 0.15}];
bmesh["Wireframe"["MeshElementStyle" -> Directive[FaceForm[MaterialShading["Aluminum"]], EdgeForm[]]]]殻化
shape = OpenCascadeShape[Cuboid[]]OpenCascadeShapeType[shape]OpenCascadeShapeNumberOfFaces[shape]shell = OpenCascadeShapeShelling[shape, 0.1, {2, 3}]OpenCascadeShapeType[shell]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shell]groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]ToElementMesh[bmesh]すべての面について全体の形状に殻化が与える影響を見ると便利なこともあれば，殻の操作を施したい面を見極める必要があることもある．そのために使えるVisualizeFaceFunctionというヘルパ関数があり，これは，索引で定義されている．
VisualizeFaceFunction[Cuboid[], OpenCascadeShapeShelling[#1, 0.1, #2]&]特徴の削ぎ落とし
OpenCascade は，形状の特徴を削ぎ落す機能を提供する．
b1 = Cuboid[{0, 0, 0}, {9, 4, 2}];
b2 = Cuboid[{0, 0, 1}, {4, 1, 2}];
b3 = Cuboid[{4, 0, 0}, {6, 2, 2}];shapes = OpenCascadeShape /@ {b1, b2, b3};
shape = OpenCascadeShapeDifference@@shapesOpenCascadeShapeType[shape]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]OpenCascadeShapeNumberOfFaces[shape]bmesh["BoundaryElementMarkerUnion"]面11と面12を強調した，境界付きのElementMeshを可視化する．
Show[bmesh["Wireframe"], bmesh["Wireframe"[ElementMarker == 11 || ElementMarker == 12, "MeshElementStyle" -> FaceForm[Orange]]]]defeatured = OpenCascadeShapeDefeaturing[shape, {11, 12}]形状を簡略化した，境界付きのElementMeshを抽出して可視化する．
bmeshDefeatured = OpenCascadeShapeSurfaceMeshToBoundaryMesh[defeatured];
bmeshDefeatured["Wireframe"["MeshElementStyle" -> FaceForm[Orange]]]面8と面12を強調した，境界付きのElementMeshを可視化する．
Show[bmesh["Wireframe"], bmesh["Wireframe"[ElementMarker == 8 || ElementMarker == 12, "MeshElementStyle" -> FaceForm[Orange]]]]defeatured = OpenCascadeShapeDefeaturing[shape, {8, 12}]形状の特徴を削ぎ落した，境界付きのElementMeshを抽出して可視化する．
bmeshDefeatured = OpenCascadeShapeSurfaceMeshToBoundaryMesh[defeatured];
bmeshDefeatured["Wireframe"["MeshElementStyle" -> FaceForm[Orange]]]OpenCascadeShapeType[defeatured]形状の簡略化
OpenCascade は，形状を簡略化する機能を提供する．
b1 = Cuboid[{2, 0, 0}, {8, 4, 2}];
b2 = Cuboid[{1, 0, 1}, {4, 1, 2}];
b3 = Cuboid[{4, -1, 0}, {6, 2, 2}];shapes = OpenCascadeShape /@ {b1, b2, b3};
shape = OpenCascadeShapeUnion@@shapesOpenCascadeShapeType[shape]OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Wireframe"]OpenCascadeShapeNumberOfFaces[shape]shape = OpenCascadeShapeSimplify[shape]OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]["Wireframe"]OpenCascadeShapeNumberOfFaces[shape]形状の治癒
OpenCascade は，形状を治す機能を提供する．例えば，曲面の壊れた順序付けを修復することができる．
OpenCascadeShapeFix[shape]インポートとエキスポート
OpenCascade は，コンピュータを使ったさまざまな設計関連のファイル形式を読み取り，書き込むことができる．これらのファイル形式のインポートとエキスポートは一部実装されている．
STLのエキスポート
OpenCascade は，STLファイルをエキスポートすることができる．
shape = OpenCascadeShape[Ball[{1, 0, 0}]]fileName = FileNameJoin[{$TemporaryDirectory, "test.stl"}];
OpenCascadeShapeExport[fileName, shape]Importを使って，生成されたSTLファイルをインポートする．
mr = Import[fileName];
bmesh = ToBoundaryMesh[mr];境界付きのElementMeshを可視化する．
bmesh["Wireframe"]OpenCascade における境界法線は，Wolfram言語におけるものとは逆方向である．エキスポートしたSTLの法線が「誤った」方向であるように見える場合には，これをElementMeshに変換し，それをMeshRegionに変換するとよい． その後MeshRegionは，Exportを使ってSTLファイルとしてエキスポートできる．
STLエキスポートのために，形状をMeshRegionに変換する．
fileName = FileNameJoin[{$TemporaryDirectory, "testMR.stl"}];
mr = MeshRegion[OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]];
Export[fileName, mr]STLのインポート
OpenCascade は，STLファイルをインポートすることができる．
shape = OpenCascadeShapeImport[FindFile["ExampleData/vase.stl"]]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]境界付きのElementMeshを可視化する．
bmesh["Wireframe"]OpenCascadeShapeImportを使ってSTLファイルをインポートすると，曲面要素のそれぞれに異なるマーカーが割り当てられた境界メッシュになることに注意する．
bmesh["BoundaryElementMarkerUnion"]//Shortこれは望ましい結果ではないかもしれない．これを避けるために，"MarkerMethod""ElementMesh"または"MarkerMethod"Noneのオプションを指定することができる．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape, "MarkerMethod" -> "ElementMesh"](groups = bmesh["BoundaryElementMarkerUnion"])//Shortマーカーをハイライトして，境界付きのElementMeshを可視化する．
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ temp
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]Stepのエキスポート
OpenCascade は，STEPファイルをエキスポートすることができる．
shape = OpenCascadeShape[Cone[{{0, 0, 0}, {0, 0, 1}}, 1]]fileName = FileNameJoin[{$TemporaryDirectory, "test.stp"}];
OpenCascadeShapeExport[fileName, shape]Stepのインポート
OpenCascade は，STEPファイルをインポートすることができる．
path = FileNameJoin[{$OpenCascadeInstallationDirectory, "ExampleData"}];shape = OpenCascadeShapeImport[FileNameJoin[{path, "screw.step"}]]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]ToElementMesh[bmesh]shape = OpenCascadeShapeImport[FileNameJoin[{path, "linkrods.step"}]]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
Rasterize[bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]]ToElementMesh[bmesh]Stepの組立ては OpenCascade Compoundsとしてインポートできる．関数OpenCascadeShapeNumberOfSolidsで数多くの組立ての立体部品を探すことができ，関数OpenCascadeShapeSolidsでその部品を抽出することができる．
BRepのエキスポート
OpenCascade は，BRepファイルをエキスポートすることができる．
shape = OpenCascadeShape[Cone[{{0, 0, 0}, {0, 0, 1}}, 1]]fileName = FileNameJoin[{$TemporaryDirectory, "test.brep"}];
OpenCascadeShapeExport[fileName, shape]BRepのインポート
OpenCascade は，BRepファイルをインポートすることができる．
path = FileNameJoin[{$OpenCascadeInstallationDirectory, "ExampleData"}];shape = OpenCascadeShapeImport[FileNameJoin[{path, "Bottom.brep"}]]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ tempマーカーを強調した，境界付きのElementMeshを可視化する．
Rasterize[bmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]]ToElementMesh[bmesh, "MeshOrder" -> 1]単位
path = FileNameJoin[{$OpenCascadeInstallationDirectory, "ExampleData"}];shape = OpenCascadeShapeImport[FileNameJoin[{path, "linkrods.step"}]]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape]bmesh["LengthUnit"]デフォルトとして OpenCascade がミリメートルの長さの単位を使うようにリクエストすることができる．
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape, "ElementMeshOptions" -> {"LengthUnit" -> "Millimeters"}]bmesh["LengthUnit"]bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape, "ElementMeshOptions" -> {"LengthUnit" -> "Meter"}]bmesh["LengthUnit"]ToElementMesh[bmesh]["LengthUnit"]考えられる問題
ブール演算の問題
OpenCascase のブール演算から得られる最も低い次元のオブジェクトは，ブール演算に与えられた任意の引数の最低次元のものである．例えば，OpenCascade の2つの立体のブール演算は，OpenCascade の面オブジェクトを返すことができない．
Graphics3D[{{Opacity[0.5], c1 = Cuboid[], c2 = Cuboid[{1, 1 / 2, 1 / 2}]}, {Red, Polygon[{{1, 1 / 2, 1 / 2}, {1, 1, 1 / 2}, {1, 1, 1}, {1, 1 / 2, 1}}]}}, Boxed -> False]s1 = OpenCascadeShape[c1]
s2 = OpenCascadeShape[c2]OpenCascadeShapeType[s1]
OpenCascadeShapeType[s2]intersection = OpenCascadeShapeIntersection[s1, s2]OpenCascadeShapeType[intersection]境界メッシュは生成できない．結果の OpenCascade の形状の共通部分には，より低次元の面オブジェクトについての情報が含まれていないからである．
OpenCascadeShapeSurfaceMeshToBoundaryMesh[intersection]OpenCascadeShapeNumberOfFaces[intersection]Graphics3D[{{Opacity[0.5], face = Polygon[{{1, 0, 0}, {1, 1, 0}, {1, 1, 1}, {1, 0, 1}}], c2}, {Red, Polygon[{{1, 1 / 2, 1 / 2}, {1, 1, 1 / 2}, {1, 1, 1}, {1, 1 / 2, 1}}]}}, Boxed -> False]s1 = OpenCascadeShape[face]
s2 = OpenCascadeShape[c2]OpenCascadeShapeType[s1]
OpenCascadeShapeType[s2]intersection = OpenCascadeShapeIntersection[s1, s2]OpenCascadeShapeType[intersection]OpenCascade の積についてのブール演算の最小次元の引数は，面オブジェクトである．結果の演算も面オブジェクトであるので，オブジェクト情報が結果の形状オブジェクトに存在し，メッシュを作成することができる．
OpenCascadeShapeSurfaceMeshToBoundaryMesh[intersection]["Wireframe"]公差の問題
OpenCascadeの標準公差は
である．その尺度の成分を持つ形状の作業を行っている場合には，形状の尺度を変更することをお勧めする．一旦形状が生成されたら，境界メッシュをもう一度もとの尺度に戻せばよい．
s1 = OpenCascadeShape[Ball[{0, 0, 0}, 10 ^ -8]];
s2 = OpenCascadeShape[Ball[{10 ^ -8, 0, 0}, 10 ^ -8]];
s = OpenCascadeShapeUnion[s1, s2];
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[s];
bmesh["Wireframe"["MeshElementStyle" -> Directive[{Opacity[0.5], FaceForm[LightGreen]}]]]オペレーティングシステムによっては，それによって欠陥が明らかになることもある．以下は欠陥が見えるものである．
OpenCascadeのデフォルト公差である
より低い公差でブール演算を行うと欠陥が生じる．
scale = 10 ^ 6;
s1 = OpenCascadeShape[Ball[{0, 0, 0}, scale * 10 ^ -8]];
s2 = OpenCascadeShape[Ball[scale * {10 ^ -8, 0, 0}, scale * 10 ^ -8]];
s = OpenCascadeShapeUnion[s1, s2];
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[s];
bmesh["Wireframe"["MeshElementStyle" -> Directive[{Opacity[0.5], FaceForm[LightGreen]}]]]bmesh["LengthUnit"]SetLengthUnit[bmesh, "Micrometers"]bmesh2 = ElementMeshCoordinateRescale[bmesh, "Meters"]bmesh2["Bounds"]一点注意したいことは，形状の尺度を変更したままにして，偏微分方程式係数を新しい長さの尺度に調整する方がこの後行う有限要素解析に役立つかもしれないということである．これは数値解の安定性を改善する．このことについては，例えば，固体力学のモノグラフに説明されている．
ユーティリティ関数
関数VisualizeEdgeFunctionは，領域のそれぞれの辺に対して，順番に操作を適用するために使える．
VisualizeEdgeFunction[region_, funIn_] := With[
{fun = funIn, ishape = OpenCascadeLink`OpenCascadeShape[region]},
With[
{numEdges = OpenCascadeLink`OpenCascadeShapeNumberOfEdges[ishape],
bmesh = OpenCascadeLink`OpenCascadeShapeSurfaceMeshToBoundaryMesh[ishape]},
Manipulate[Module[{shape, newShape},
shape = OpenCascadeLink`OpenCascadeShape[region];
newShape = fun[shape, edge];
Show[
bmesh["Edgeframe"["EdgeframeDirective" -> LightGray]],
If[newShape === $Failed,
{}
, OpenCascadeLink`OpenCascadeShapeSurfaceMeshToBoundaryMesh[newShape]["Edgeframe"]
]
, PlotLabel -> Style["Edge = " <> ToString[edge]]
]
], {edge, 1, numEdges, 1, Appearance -> "Open"}, Initialization :> (Needs["OpenCascadeLink`"])]
]
]関数VisualizeFaceFunctionは，領域のそれぞれの面に対して，順番に操作を適用するために使える．
VisualizeFaceFunction[region_, funIn_] := With[
{fun = funIn, ishape = OpenCascadeLink`OpenCascadeShape[region]},
With[
{numFaces = OpenCascadeLink`OpenCascadeShapeNumberOfFaces[ishape],
bmesh = OpenCascadeLink`OpenCascadeShapeSurfaceMeshToBoundaryMesh[ishape]},
Manipulate[Module[{shape, newShape, newBmesh, groups, temp, colors},
shape = OpenCascadeLink`OpenCascadeShape[region];
newShape = fun[shape, face];
Show[
bmesh["Edgeframe"["EdgeframeDirective" -> LightGray]],
If[newShape === $Failed,
{}
,
newBmesh = OpenCascadeLink`OpenCascadeShapeSurfaceMeshToBoundaryMesh[newShape];
groups = newBmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1 / (Length[groups])]];
colors = ColorData["BrightBands"][#]& /@ temp;
newBmesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]
]
, PlotLabel -> Style["Face = " <> ToString[face]]
]
], {face, 1, numFaces, 1, Appearance -> "Open"}, Initialization :> (Needs["OpenCascadeLink`"])]
]
]