ListVectorDisplacementPlot[{{{vx11,vy11},…,{vx1n,vy1n}},…,{{vxm1,vym1},…,{vxmn,vymn}}}]
generates a displacement plot from an array of vector displacements {vxij,vyij}.
ListVectorDisplacementPlot[{{{x1,y1},{vx1,vy1}},…,{{x1,y1},{vx1,vy1}}}]
generates a displacement plot from displacements {vxi,vyi} at point {xi,yi}.
ListVectorDisplacementPlot[{{ {{vx11,vy11},s11},…,{{vx1n,vy1n},s1n}},…,{ {{vxmi,vym1},sm1},…,{{vxmn,vymn},smn}}}]
uses the scalar values sij to color the displaced region.
ListVectorDisplacementPlot[{ {{vx1,vy1},s1},…,{{vxn,vyn},sn}}]
uses the scalar values si at point {xi,yi} to color the displaced region.
ListVectorDisplacementPlot[…,reg]
plots the displacement over the region reg.




ListVectorDisplacementPlot
ListVectorDisplacementPlot[{{{vx11,vy11},…,{vx1n,vy1n}},…,{{vxm1,vym1},…,{vxmn,vymn}}}]
generates a displacement plot from an array of vector displacements {vxij,vyij}.
ListVectorDisplacementPlot[{{{x1,y1},{vx1,vy1}},…,{{x1,y1},{vx1,vy1}}}]
generates a displacement plot from displacements {vxi,vyi} at point {xi,yi}.
ListVectorDisplacementPlot[{{ {{vx11,vy11},s11},…,{{vx1n,vy1n},s1n}},…,{ {{vxmi,vym1},sm1},…,{{vxmn,vymn},smn}}}]
uses the scalar values sij to color the displaced region.
ListVectorDisplacementPlot[{ {{vx1,vy1},s1},…,{{vxn,vyn},sn}}]
uses the scalar values si at point {xi,yi} to color the displaced region.
ListVectorDisplacementPlot[…,reg]
plots the displacement over the region reg.
Details and Options



- ListVectorDisplacementPlot generates a displacement plot using the vector field data over a region. By default, the size of the displacement is automatically scaled so that both small and large displacements remain visible. The displaced region is by default colored according to the magnitude of the displacement.
- If no scalar field values are given, they are taken to be the norm of the vector field.
- ListVectorDisplacementPlot by default interpolates the data given and plots vectors for the vector field at a regular grid of positions.
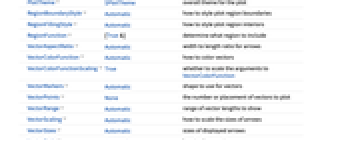
- ListVectorDisplacementPlot has the same options as Graphics, with the following additions and changes: [List of all options]
-
AspectRatio 1 ratio of height to width BoundaryStyle None how to draw RegionFunction boundaries ClippingStyle Automatic how to display arrows outside the vector range ColorFunction Automatic how to color background densities ColorFunctionScaling True whether to scale arguments to ColorFunction DataRange Automatic the range of x and y values to assume for data Frame True whether to draw a frame around the plot FrameTicks Automatic frame tick marks Mesh None how many mesh lines to draw in the background MeshFunctions {#5&} how to determine the placement of mesh lines MeshStyle Automatic the style of mesh lines Method Automatic methods to use for the plot PerformanceGoal $PerformanceGoal aspects of performance to try to optimize PlotLegends None legends for color gradients PlotRange {Full,Full} range of x, y values to include PlotRangePadding Automatic how much to pad the range of values PlotTheme $PlotTheme overall theme for the plot RegionBoundaryStyle Automatic how to style plot region boundaries RegionFillingStyle Automatic how to style plot region interiors RegionFunction (True&) determine what region to include VectorAspectRatio Automatic width to length ratio for arrows VectorColorFunction Automatic how to color vectors VectorColorFunctionScaling True whether to scale the arguments to VectorColorFunction VectorMarkers Automatic shape to use for vectors VectorPoints None the number or placement of vectors to plot VectorRange Automatic range of vector lengths to show VectorScaling Automatic how to scale the sizes of arrows VectorSizes Automatic sizes of displayed arrows VectorStyle Automatic how to draw vectors - The arguments supplied to functions in MeshFunctions, RegionFunction, ColorFunction and VectorColorFunction are x, y, vx, vy, s.
- The default setting MeshFunctions{#5&} draws mesh lines for the scalar field s.
- By default, the displacement plot shows a representation of the original region and the displaced region.
- RegionBoundaryStyle and RegionFillingStyle can be used to change the style of the original region.
- Additional settings for VectorPoints to show displacement arrows include:
-
Automatic automatically chosen points All use the original data points "Boundary" points along the boundary of reg - By default, displacement arrows connect locations in the original region with the corresponding displaced locations.
- VectorSizesFull shows the full displacement rather than a scaled representation.
-
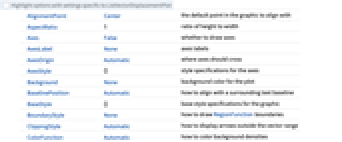
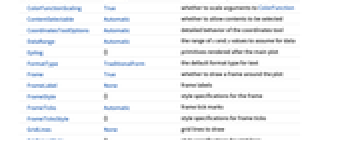
AlignmentPoint Center the default point in the graphic to align with AspectRatio 1 ratio of height to width Axes False whether to draw axes AxesLabel None axes labels AxesOrigin Automatic where axes should cross AxesStyle {} style specifications for the axes Background None background color for the plot BaselinePosition Automatic how to align with a surrounding text baseline BaseStyle {} base style specifications for the graphic BoundaryStyle None how to draw RegionFunction boundaries ClippingStyle Automatic how to display arrows outside the vector range ColorFunction Automatic how to color background densities ColorFunctionScaling True whether to scale arguments to ColorFunction ContentSelectable Automatic whether to allow contents to be selected CoordinatesToolOptions Automatic detailed behavior of the coordinates tool DataRange Automatic the range of x and y values to assume for data Epilog {} primitives rendered after the main plot FormatType TraditionalForm the default format type for text Frame True whether to draw a frame around the plot FrameLabel None frame labels FrameStyle {} style specifications for the frame FrameTicks Automatic frame tick marks FrameTicksStyle {} style specifications for frame ticks GridLines None grid lines to draw GridLinesStyle {} style specifications for grid lines ImageMargins 0. the margins to leave around the graphic ImagePadding All what extra padding to allow for labels etc. ImageSize Automatic the absolute size at which to render the graphic LabelStyle {} style specifications for labels Mesh None how many mesh lines to draw in the background MeshFunctions {#5&} how to determine the placement of mesh lines MeshStyle Automatic the style of mesh lines Method Automatic methods to use for the plot PerformanceGoal $PerformanceGoal aspects of performance to try to optimize PlotLabel None an overall label for the plot PlotLegends None legends for color gradients PlotRange {Full,Full} range of x, y values to include PlotRangeClipping False whether to clip at the plot range PlotRangePadding Automatic how much to pad the range of values PlotRegion Automatic the final display region to be filled PlotTheme $PlotTheme overall theme for the plot PreserveImageOptions Automatic whether to preserve image options when displaying new versions of the same graphic Prolog {} primitives rendered before the main plot RegionBoundaryStyle Automatic how to style plot region boundaries RegionFillingStyle Automatic how to style plot region interiors RegionFunction (True&) determine what region to include RotateLabel True whether to rotate y labels on the frame Ticks Automatic axes ticks TicksStyle {} style specifications for axes ticks VectorAspectRatio Automatic width to length ratio for arrows VectorColorFunction Automatic how to color vectors VectorColorFunctionScaling True whether to scale the arguments to VectorColorFunction VectorMarkers Automatic shape to use for vectors VectorPoints None the number or placement of vectors to plot VectorRange Automatic range of vector lengths to show VectorScaling Automatic how to scale the sizes of arrows VectorSizes Automatic sizes of displayed arrows VectorStyle Automatic how to draw vectors
List of all options


Examples
open all close allBasic Examples (4)
Scope (15)
Sampling (8)
Visualize a scaled displacement field by comparing a reference and a deformed region:
Specify the coordinates and the vector field:
Specify the coordinates, the vector field and a scalar field:
Generate random points in a vector field:
By default, the reference region is the convex hull of the coordinates:
Vectors are drawn from points in the reference region to corresponding points in the (scaled) deformed region:
Restrict vectors to points on the boundary:
Displacements can be drawn to scale:
Specify the region with a RegionFunction:
The domain may be an ImplicitRegion:
The domain may be a ParametricRegion:
The domain may be a MeshRegion:
The domain may be a BoundaryMeshRegion:
Presentation (7)
Specify the ColorFunction for the deformed region:
Specify the VectorColorFunction independently of the ColorFunction:
Use a single color for the arrows:
Include a legend for the norms of the displacements:
Include a legend for the optional scalar field:
Include a Mesh:
Options (45)
AspectRatio (2)
BoundaryStyle (3)
By default, the boundary style matches the interior colors in the deformed region:
Specify the BoundaryStyle:
BoundaryStyle applies to regions cut by RegionFunction:
ColorFunction (4)
By default, the deformed region is colored by the norm of the field:
Specify a scalar field for the colors:
Specify a custom ColorFunction:
ColorFunctionScaling (2)
Use the natural range of norm values:
Control the scaling of the individual arguments of the ColorFunction:
DataRange (1)
Mesh (3)
Specify a Mesh to visualize the displacements:
Show the initial and final sampling mesh:
Specify 10 mesh lines in the ![]() direction and 5 in the
direction and 5 in the ![]() direction:
direction:
Use mesh lines at specific values:
Highlight specific mesh lines:
Mesh lines are suppressed in the reference region if the boundary and filling of the reference region are removed:
MeshFunctions (1)
PlotLegends (3)
PlotRange (3)
The full PlotRange is used by default:
Specify an explicit limit that is shared by the ![]() and
and ![]() directions:
directions:
PlotStyle (4)
Remove the filling for the deformed region:
Apply a Texture to the deformed region:
Use PatternFilling to style the deformed region:
ColorFunction has precedence over PlotStyle:
RegionBoundaryStyle (2)
RegionFillingStyle (2)
RegionFunction (1)
Use a RegionFunction to specify the reference region:
VectorAspectRatio (2)
VectorColorFunction (1)
By default, if VectorColorFunction is Automatic, then the VectorColorFunction matches the ColorFunction:
Specify a VectorColorFunction that is different from the ColorFunction:
Use no VectorColorFunction:
VectorMarkers (1)
VectorPoints (2)
No vectors are shown by default:
Show vectors sampled from the entire original region:
Sample vectors from the boundary of the region:
Use symbolic names to specify the density of vectors:
Use symbolic names to specify the arrangement of vectors:
Specify the number of vectors in the ![]() and
and ![]() directions:
directions:
Specify a different number of vectors in the ![]() and
and ![]() directions:
directions:
VectorScaling (1)
VectorSizes (1)
By default, vectors extend from points in the reference region to corresponding points in the deformed region:
Specify the range of arrow lengths:
Suppress scaling of the displacement vectors so that a rotation of 45° looks appropriate:
Suppress scaling of the displacement vectors even if no vectors are displayed:
VectorStyle (1)
VectorColorFunction has precedence over VectorStyle:
Applications (17)
Basic Applications (16)
A constant displacement field moves each point in the reference region by the same amount:
Note that the displacements are automatically scaled so that very small and very large displacements are both visible:
Use VectorSizesFull to display the actual sizes of displacements:
Color is used to indicate the magnitude of the displacements:
Color the region by a different scalar function:
Use arrows to indicate initial and final locations for a sample points:
Visualize a dilation in the ![]() direction:
direction:
Visualize a contraction in the ![]() direction:
direction:
Visualize a dilation in the ![]() direction and a contraction in the
direction and a contraction in the ![]() direction:
direction:
Visualize a shear in the ![]() direction:
direction:
Visualize a shear in the ![]() direction:
direction:
Visualize a combined shear in the ![]() and
and ![]() directions:
directions:
Visualize a rotation about the origin:
Combine a rotation, a shear and a dilation:
Solid Mechanics (1)
The left edge of the displayed region is fixed (no displacement) and a uniform horizontal load of 10 kPa is applied the right edge:
Obtain data from a numerical solver of the form {location vector, {displacement vector, Frobenius norm of stress tensor}} assuming that the region is linearly elastic and in plane stress:
Use a RegionFunction to properly visualize the deformed region. Note the stresses near the unloaded corners are much higher than the applied load of 10 kPa:
Properties & Relations (12)
Use ListVectorDisplacementPlot3D to visualize deformations in 3D:
Use VectorDisplacementPlot to visualize functions:
Use VectorDisplacementPlot3D to visualize functions in 3D:
Use ListVectorPlot for plotting data:
Use ListStreamPlot to plot streamlines instead of vectors:
Use StreamPlot to plot with streamlines instead of vectors:
Use VectorDensityPlot to add a density plot of the scalar field:
Use ListVectorDensityPlot or ListStreamDensityPlot to add a density plot of a scalar field:
Use LineIntegralConvolutionPlot to plot the line integral convolution of a vector field:
Use ListVectorPlot3D or ListStreamPlot3D to visualize vector fields in 3D:
Use VectorPlot3D and StreamPlot3D to visualize 3D vector fields:
Plot vectors on surfaces with SliceVectorPlot3D:
Plot complex functions as a vector field:
Use ComplexStreamPlot to plot streamlines instead of vectors:
Use GeoVectorPlot to plot vectors on a map:
Use GeoStreamPlot to plot streamlines instead of vectors:
Related Guides
History
Text
Wolfram Research (2021), ListVectorDisplacementPlot, Wolfram Language function, https://reference.wolfram.com/language/ref/ListVectorDisplacementPlot.html.
CMS
Wolfram Language. 2021. "ListVectorDisplacementPlot." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ListVectorDisplacementPlot.html.
APA
Wolfram Language. (2021). ListVectorDisplacementPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ListVectorDisplacementPlot.html
BibTeX
@misc{reference.wolfram_2025_listvectordisplacementplot, author="Wolfram Research", title="{ListVectorDisplacementPlot}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/ListVectorDisplacementPlot.html}", note=[Accessed: 25-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_listvectordisplacementplot, organization={Wolfram Research}, title={ListVectorDisplacementPlot}, year={2021}, url={https://reference.wolfram.com/language/ref/ListVectorDisplacementPlot.html}, note=[Accessed: 25-February-2026]}