QuantilePlot
QuantilePlot[list]
list の分位点と正規分布の分位点を比較するプロットを生成する.
QuantilePlot[dist]
分布 dist の分位点と正規分布の分位点を比較するプロットを生成する.
QuantilePlot[data,rdata]
data と rdata の分位点を比較するプロットを生成する.
QuantilePlot[data,rdist]
data の分位点と記号分布 rdist の分位点を比較するプロットを生成する.
QuantilePlot[{data1,data2,…},ref]
datai の分位点と基準分布 ref の分位点を比較するプロットを生成する.
詳細とオプション




- QuantilePlotは,1引数の形の正規分位点プロットおよび2引数の形のQ-Qプロットとしても知られている.
- QuantilePlot[data1,data2]は実数値のデータ集合か一変量記号分布である dataiに使うことができる.
- QuantilePlot用のデータは次の形式で与えることができる.
-
{e1,e2,…} ラッパーがある/ない要素のリスト <k1y1,k2y2,…> キーと長さの連想 TimeSeries[…],EventSeries[…],TemporalData[…] 時系列,事象系列,一時データ WeightedData[…],EventData[…] 拡張データ集合 w[{e1,e2,…},…] データ集合全体に適用されたラッパー w[{data1,data1,…},…] すべてのデータ集合に適用されたラッパー - データ集合 list には経験的分位点が使われ,記号分布 dist には厳密な分位点が使われる.
- 記号母数 θiを持つQuantilePlot[data,dist[θ1,…]]はQuantilePlot[data,EstimatedDistribution[data,dist[θ1,…]]]に等しい.
- w[data]または w[dist]の形式で結果のグラフィッスプリミティブに適用するラッパー w を与える.
- QuantilePlot[Tabular[…]cspec]は,列指定 cspec を使って表オブジェクトから値を抽出し,これをプロットする.
- 次は,表データのプロットに使用可能な列指定 cspecの形式である.
-
colx 列 x からの値をプロットする {colx1,colx2,…} 列 x1, x2, …をプロットする - 使用可能なラッパー
-
Annotation[e,label] 注釈を与える Button[e,action] 要素がクリックされたときに実行されるアクションを定義 EventHandler[e,…] 要素の一般的なイベントハンドラを定義 Highlighted[datai,effect] 効果を使って fiを動的にハイライトする Highlighted[datai,Placed[effect,pos]] 位置 pos で効果を使って fiを静的にハイライトする Hyperlink[e,uri] 要素をハイパーリンクにする PopupWindow[e,cont] 要素にポップアップウィンドウを付加 StatusArea[e,label] 要素上にマウスが置かれたときにステータスエリアに表示 Style[e,opts] 指定のスタイルで要素を表示 Tooltip[e,label] 要素に任意のツールチップを付加 - QuantilePlotにはGraphicsと同じオブションに以下の追加・変更を加えたものが使える. [全オプションのリスト]
-
AspectRatio 1/GoldenRatio 縦横比 ClippingStyle Automatic 曲線が切断された箇所に何を描くか ColorFunction Automatic 曲線の彩色をどのように決めるか ColorFunctionScaling True ColorFunctionの引数をスケールするかどうか Filling None 各曲線の下に挿入する塗潰し FillingStyle Automatic 塗潰しに使用するスタイル Joined Automatic 点を繋ぐかどうか Mesh None 各曲線にいくつのメッシュ点を描くか MeshFunctions {#1&} メッシュ点の置き方をどう決めるか MeshShading None メッシュ点の間の領域にどのように陰影を付けるか MeshStyle Automatic メッシュ点のスタイル Method Automatic 使用するメソッド PerformanceGoal $PerformanceGoal パフォーマンスのどの面について最適化するか PlotHighlighting Automatic 曲線のハイライト効果 PlotLegends None データ点の凡例 PlotMarkers None データ集合の各点を示すためのマーカー PlotRange Automatic 含める値の範囲 PlotRangeClipping True プロット範囲で切断するかどうか PlotStyle Automatic 各オブジェクトのスタイルを指定するグラフィックス指示子 PlotTheme $PlotTheme プロットの全体的なテーマ ReferenceLineStyle Automatic 基準線のスタイル ScalingFunctions None 個々の座標をどのようにスケールするか WorkingPrecision MachinePrecision 記号分布の内部計算に使う精度 - Filling->Automaticのとき,データ集合と基準線の間は塗り潰される.デフォルトで,データ集合には「ステム」が,記号分布には「固体」塗潰しが使われる.Joined->Trueと設定するとデータ集合にも「固体」が使われるようになる.
- MeshFunctionsとRegionFunctionの関数に渡される引数は
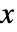 と
と 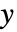 である.ColorFunctionの関数には,デフォルトでこれらの引数のスケールされたものが渡される.
である.ColorFunctionの関数には,デフォルトでこれらの引数のスケールされたものが渡される. - JoinedAutomaticは,2つの分布を比較している場合はJoinedTrueに等しく,その他の場合はJoinedFalseに等しい.
- PlotStyle->Automaticと設定すると異なる線には一連の異なるプロットスタイルが使われる.
- ReferenceLineStyle->Noneとすると,基準線は描かれない.
- 次は,HighlightedとPlotHighlightingに使用可能なハイライト効果である.
-
style 指定されたデータをハイライトする 
"Ball" データの指定された点をハイライトしてラベルを付ける 
"Dropline" データの指定された点を軸までのドロップラインでハイライトしてラベルを付ける 
"XSlice" 垂直スライスに沿ったすべての点をハイライトしてラベルを付ける 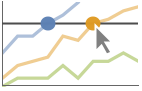
"YSlice" 水平スライスに沿ったすべての点をハイライトしてラベルを付ける 
Placed[effect,pos] 指定の位置 pos を静的にハイライトする - ハイライトの位置指定 pos には次がある.
-
x, {x} {x,y}における効果.y は自動的に選択される {x,y} {x,y}における効果 {pos1,pos2,…} 複数の位置 posi - PlotLegendsのよく使われる設定値
-
None 凡例は使わない Automatic 凡例を自動的に決定する {lbl1,lbl2,…} lbl1, lbl2, … を凡例ラベルとして使う Placed[lspec,…] 凡例の置き方を指定する - ScalingFunctions->{sx,sy}では,
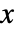 座標は sxを使ってスケールされ,
座標は sxを使ってスケールされ,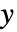 座標は syを使ってスケールされる.
座標は syを使ってスケールされる.
全オプションのリスト

例題
すべて開くすべて閉じるスコープ (25)
データと分布 (11)
QuantilePlotは数値データに使うことができる:
QuantilePlotは記号分布に使うことができる:
デフォルトの基準分布はNormalDistributionに最も近い推定分布である:
数値によるキーと連想中の値 ![]() 座標および
座標および ![]() 座標として用いられる:
座標として用いられる:
WeightedData中の重みは無視される:
表形式データ (1)
PivotToColumnsを使って種ごとの"SepalWidth"(萼片の長さ)の列を生成する:
オプション (84)
ColorFunction (6)
ColorFunctionにJoinedを使うためには少なくとも1つのデータ集合が必要である:
ColorFunctionは曲線の色付けについてはPlotStyleよりも優先順位が高い:
MeshShadingにAutomaticを使い,ColorFunctionとともに用いる:
Filling (7)
Mesh (4)
MeshShading (6)
Noneを使って線分を取り除く:
MeshShadingはPlotStyleと一緒に使うことができる:
MeshShadingは曲線のスタイル付けではPlotStyleよりも優先順位が高い:
MeshShadingをAutomaticに設定して,PlotStyleをいくつかの線分に使う:
MeshShadingをColorFunctionと一緒に使う:
PlotHighlighting (9)
デフォルト設定のPlotHighlightingAutomaticのとき,プロットにはインタラクティブな座標のコールアウトが付く:
PlotHighlightingNoneを使ってプロット全体のハイライトをオフにする:
点集合にマウスオーバーして任意のグラフィックス指示子でハイライトする:
曲線にマウスオーバーして軸までのドロップラインとラベルでハイライトする:
プロットにマウスオーバーして ![]() 位置に対応する
位置に対応する ![]() の値を示すスライスでハイライトする:
の値を示すスライスでハイライトする:
プロットにマウスオーバーして ![]() 位置に対応する
位置に対応する ![]() の値を示すスライスでハイライトする:
の値を示すスライスでハイライトする:
マウスカーソルの ![]() 位置に最も近いプロット上の点を示す成分を使う:
位置に最も近いプロット上の点を示す成分を使う:
Calloutオプションを使ってラベルの外観を変える:
PlotLegends (7)
Placedを使って凡例の置き方を指定する:
LineLegendを使って凡例の外観を変える:
PlotMarkers (7)
QuantilePlotは通常色分けしてデータ集合を区別する:
PlotRange (3)
ReferenceLineStyle (4)
ReferenceLineStyleはデフォルトでPlotStyleのDotted形式を使う:
Noneを使って基準線が描かれなくする:
ReferenceLineStyleをPlotStyleと組み合せることができる:
アプリケーション (5)
線形性からの逸脱はデータが基準分布に従っていない場合に見られる:
LinearModelFitからの剰余は正規分布に従う.ここでは,データが等分散の正規ノイズおよび指数的ノイズを使ってシミュレーションされている:
最初のモデルでは剰余が正規分布に従っていないことが視覚的にはっきりする:
DistributionFitTestを使って正規性に関する数量面の言及を行うことができる:
ニューヨークコラールソサエティに所属する歌手の身長が各人の声部とともに記録された.声部は低い方から順にバス,テノール,アルト,ソプラノである:
ソプラノ1の身長を他の声部に対してプロットすると声部に追加的なシフトがあることが分かる:
52の雲からの降雨をエーカーフィート単位で記録し,そのうち26をランダムに選び酸化銀でシードした:
明らかに,シードされた雲の方が制御グループより多くの雨を発生させる:
特性と関係 (9)
UniformDistribution[{0,1}]と比較することは分位数をプロットすることと同じである:
ProbabilityPlotはデータの累積分布関数の値を比較する:
ProbabilityScalePlotは軸をスケールして分布からの点が直線に並ぶようにする:
BoxWhiskerChartとDistributionChartを使ってデータの分布を可視化することができる:
SmoothHistogramとHistogramを使ってデータの分布を可視化することができる:
DiscretePlotを使って離散分布を可視化することができる:
ListPlotを使ってデータを見る:
QuantilePlotは,入力がTimeSeriesのときはタイムスタンプを無視する:
テキスト
Wolfram Research (2010), QuantilePlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/QuantilePlot.html (2025年に更新).
CMS
Wolfram Language. 2010. "QuantilePlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/QuantilePlot.html.
APA
Wolfram Language. (2010). QuantilePlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/QuantilePlot.html