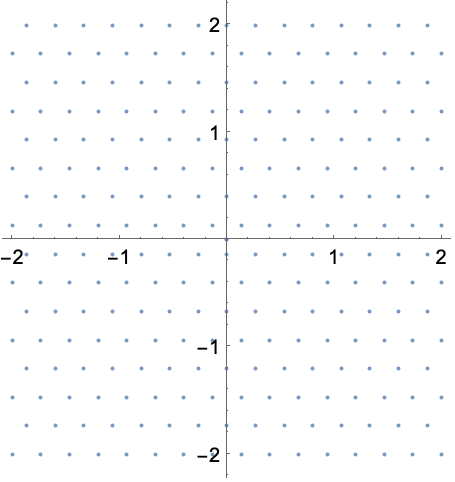
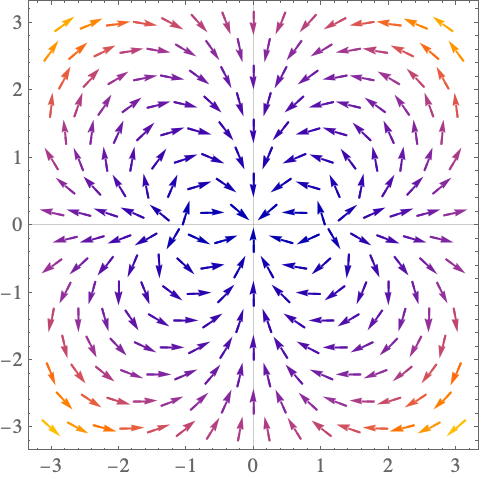
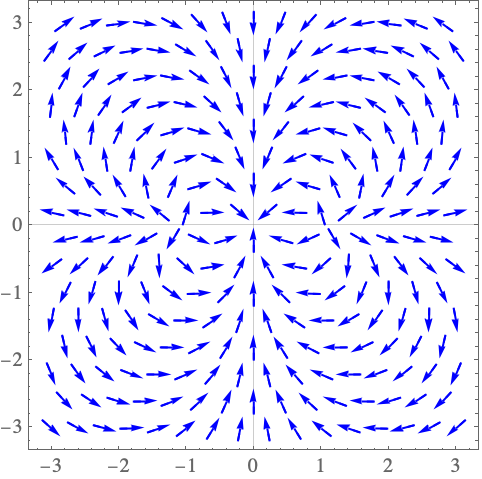
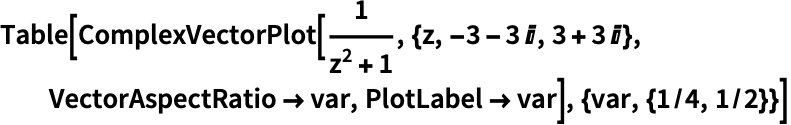ComplexVectorPlot
✖
ComplexVectorPlot
更多信息和选项


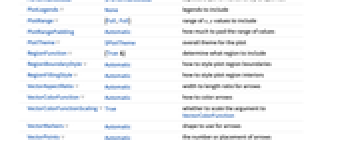

- ComplexVectorPlot 亦称为场图或方向图.
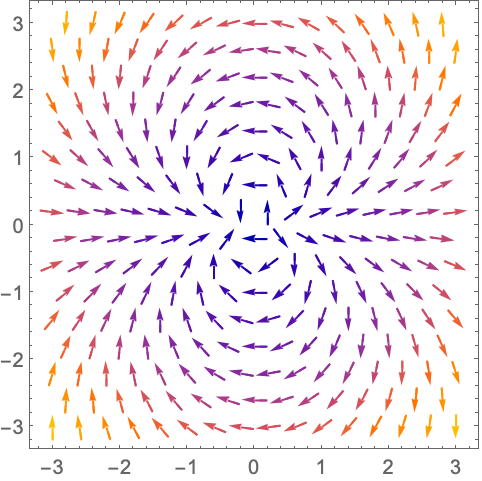
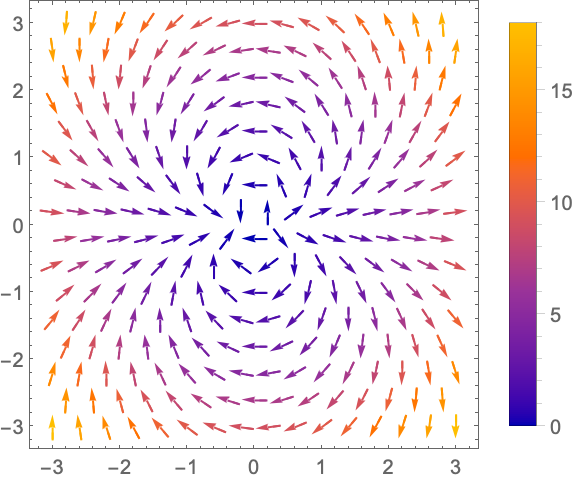
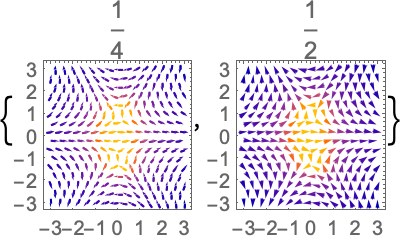
- ComplexVectorPlot 通过绘制箭头来显示向量场. 默认情况下,向量的方向由箭头的方向表示,幅值由颜色表示.
- ComplexVectorPlot 在对 f 的值进行计算后,在结果不是复数的位置处不显示箭头.
- ComplexVectorPlot[f,{z,n}] 等价于 ComplexVectorPlot[f,{z,-n-n I,n+n I}].
- ComplexVectorPlot 将变量 z 视为局部变量,相当于使用 Block.
- ComplexVectorPlot 具有属性 HoldAll,只在对 z 赋值后才计算 f. 某些情况下,先用 Evaluate 对 f 进行符号式计算效率更高.
- ComplexVectorPlot 和 Graphics 有相同的选项,不同之处和更多选项如下所示: [所有选项的列表]
-
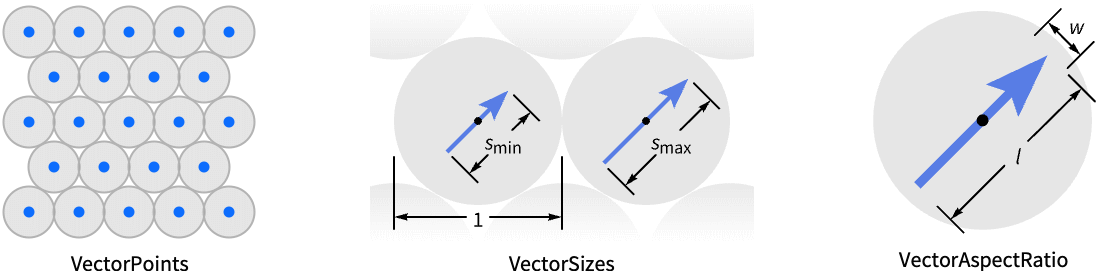
AspectRatio 1 高宽比 ClippingStyle Automatic 怎样显示向量范围之外的箭头 EvaluationMonitor None 每次运行函数时要计算的表达式 Frame True 是否为图形绘制边框 FrameTicks Automatic 边框刻度标记 Method Automatic 使用何种方法绘图 PerformanceGoal $PerformanceGoal 优化的目标 PlotLegends None 要包含的图例 PlotRange {Full,Full} 包括的 x、y 值的范围 PlotRangePadding Automatic 对数值范围进行多少填充 PlotTheme $PlotTheme 绘图的整体外观主题 RegionFunction (True&) 确定要包含的区域 RegionBoundaryStyle Automatic 怎样设置绘图区域边界的样式 RegionFillingStyle Automatic 怎样设置绘图区域内部的样式 VectorAspectRatio Automatic 箭头的宽度与长度的比 VectorColorFunction Automatic 如何为箭头着色 VectorColorFunctionScaling True 是否缩放传递给 VectorColorFunction 的函数 VectorMarkers Automatic 箭头的形状 VectorPoints Automatic 箭头的数量或放置方式 VectorRange Automatic 显示出来的向量的长度范围 VectorScaling None 怎样缩放箭头的大小 VectorSizes Automatic 显示出来的箭头的大小 VectorStyle Automatic 怎样设置箭头的样式 WorkingPrecision MachinePrecision 内部计算使用的精度 - 按比例缩放各个箭头以适应每个点周围的边界圆.
- VectorPoints{c1,c2,…} 在复数点 c1、c2、… 处绘制箭头.
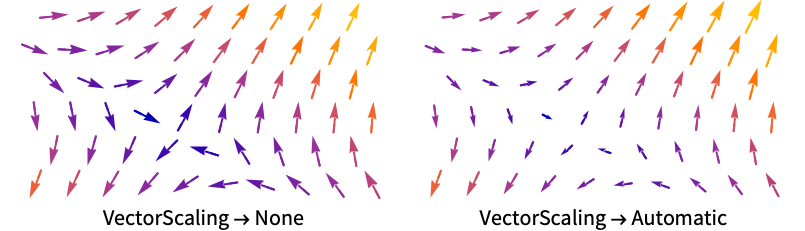
- VectorScaling 将向量的幅值缩放到 VectorSizes 给定的箭头大小范围:smin 到 smax.
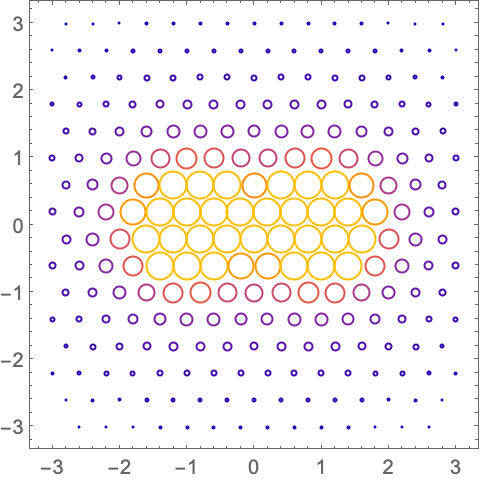
- VectorScaling->Automatic 将根据向量幅值缩放箭头的长度:
- 由 VectorMarkers 给定的箭头符号被绘制在一个方框内,方框的宽度和长度的比例为由 VectorAspectRatio 指定的
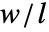 .
. - 常见的标记有:
-

"Segment" 与场方向一致的线段 
"PinDart" 沿场方向的销镖形 
"Dart" 镖形标记 
"Drop" 水滴形标记 - VectorColorFunction->None 将按 VectorStyle 指定的样式绘制箭头.
- 提供给 RegionFunction 和 VectorColorFunction 中的函数的参数为 z 和 f.
所有选项的列表


范例
打开所有单元关闭所有单元基本范例 (3)常见实例总结
范围 (19)标准用法实例范围调查
采样 (7)
https://wolfram.com/xid/0n4i0sam2ea-bnkdo9
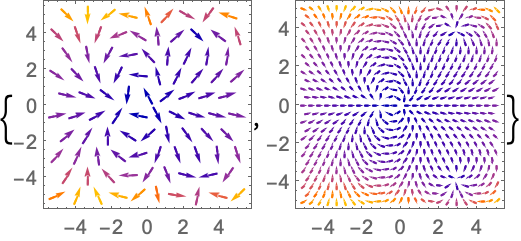
https://wolfram.com/xid/0n4i0sam2ea-jnswso
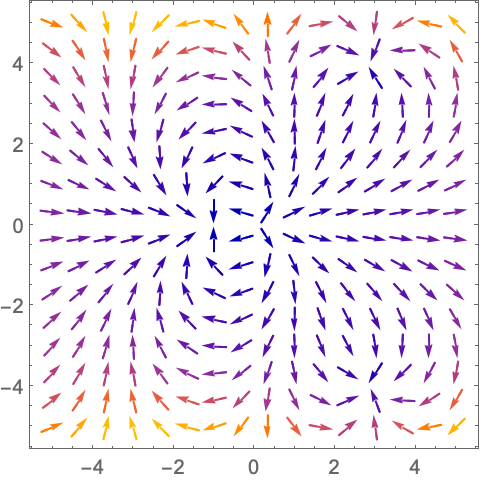
https://wolfram.com/xid/0n4i0sam2ea-gm12d0
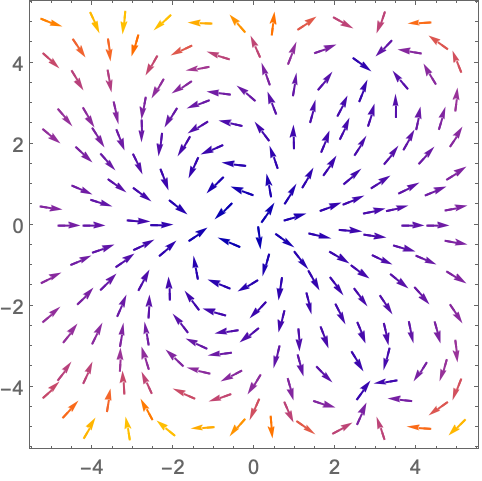
https://wolfram.com/xid/0n4i0sam2ea-6tjb00
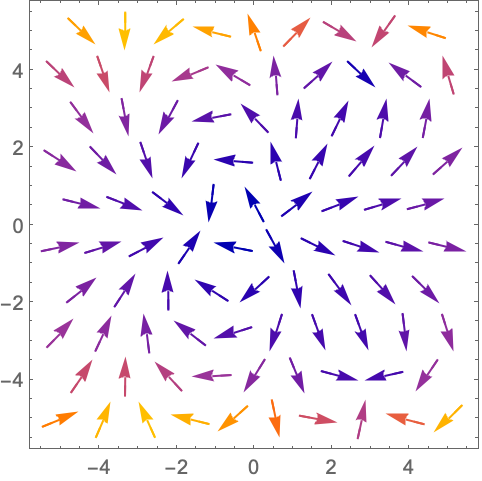
https://wolfram.com/xid/0n4i0sam2ea-bpn1i8
https://wolfram.com/xid/0n4i0sam2ea-howfal
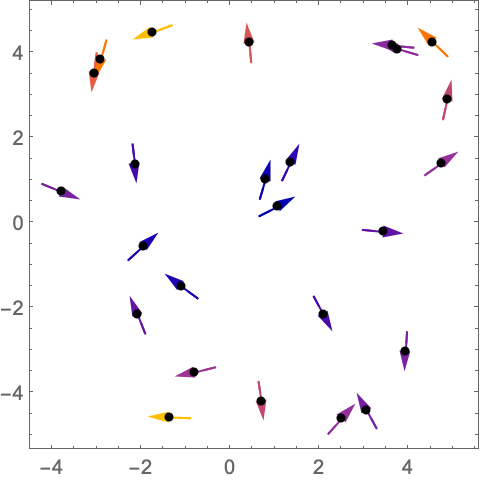
https://wolfram.com/xid/0n4i0sam2ea-lvahe5
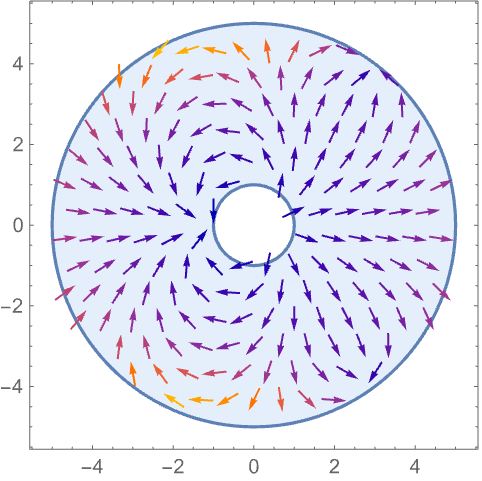
https://wolfram.com/xid/0n4i0sam2ea-zc12x
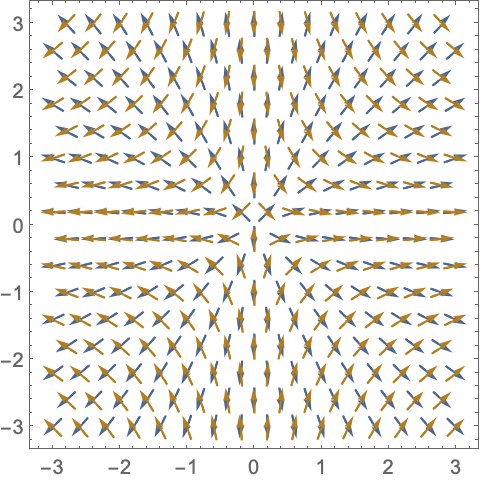
在赋值前用 Evaluate 符号式计算向量场:
https://wolfram.com/xid/0n4i0sam2ea-dzznsr
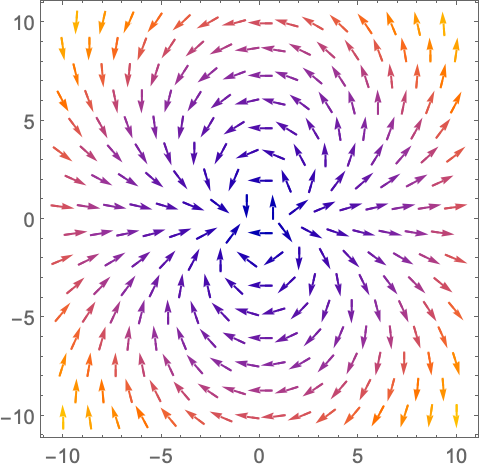
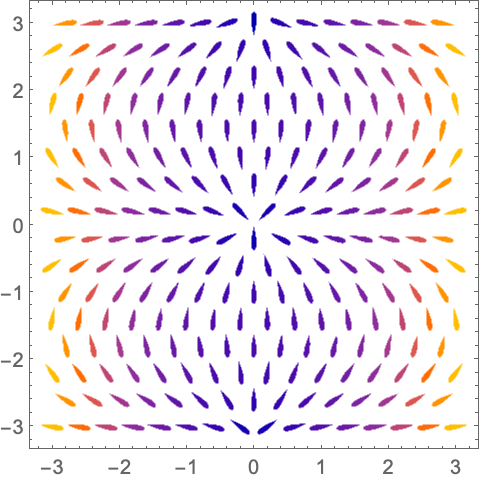
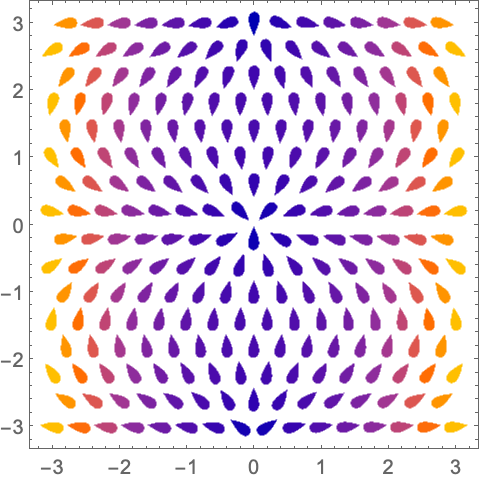
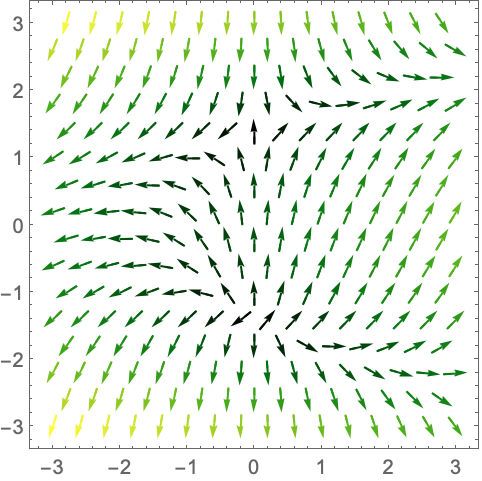
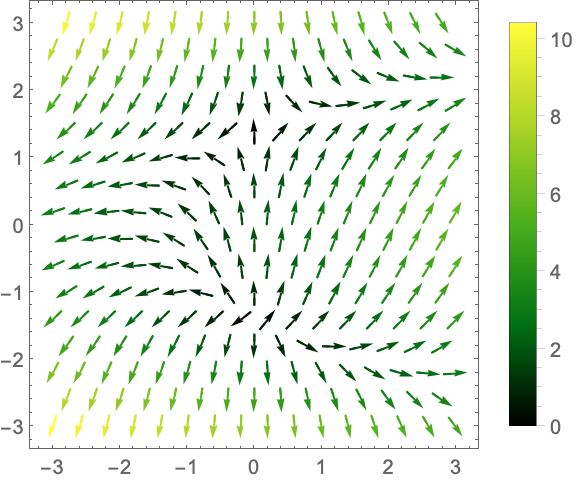
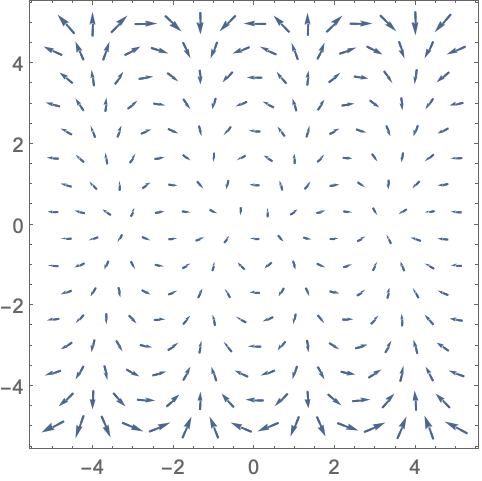
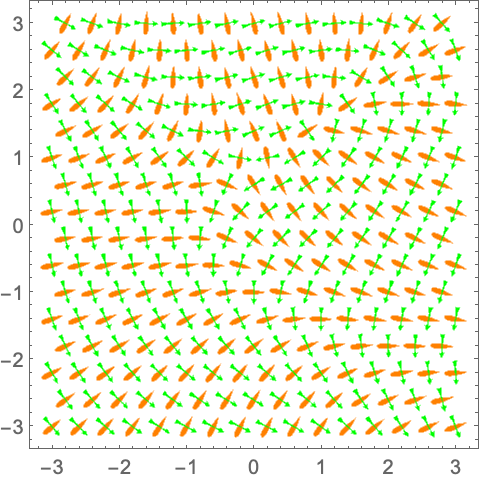
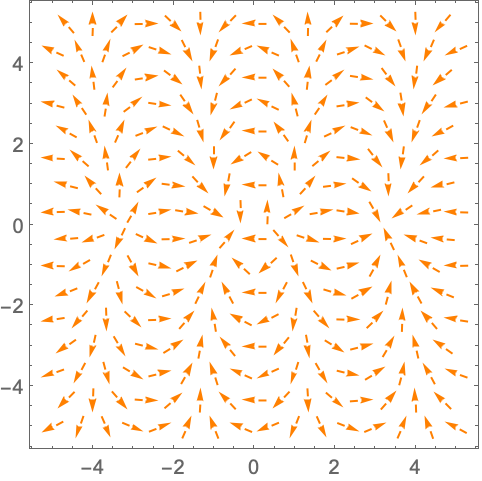
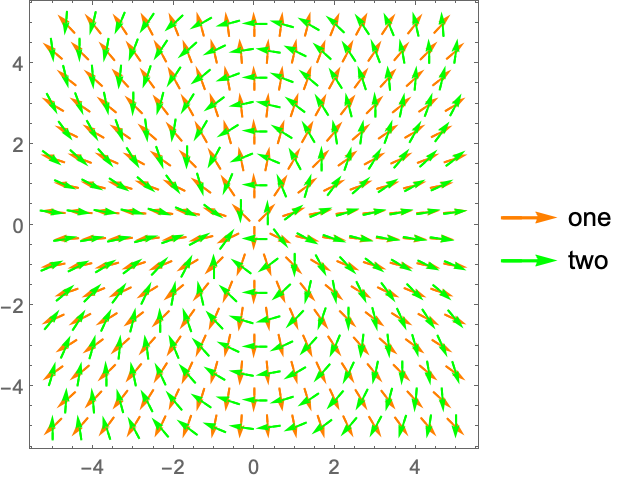
演示 (12)
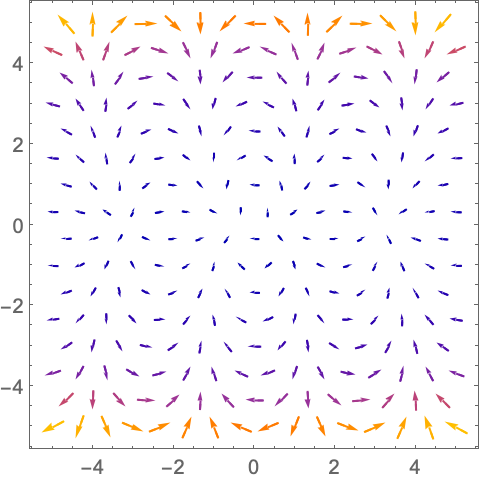
https://wolfram.com/xid/0n4i0sam2ea-bs9khg
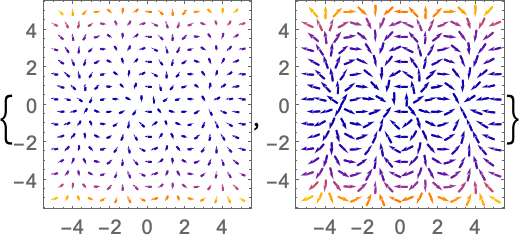
https://wolfram.com/xid/0n4i0sam2ea-3obw1y
https://wolfram.com/xid/0n4i0sam2ea-y0g4bu
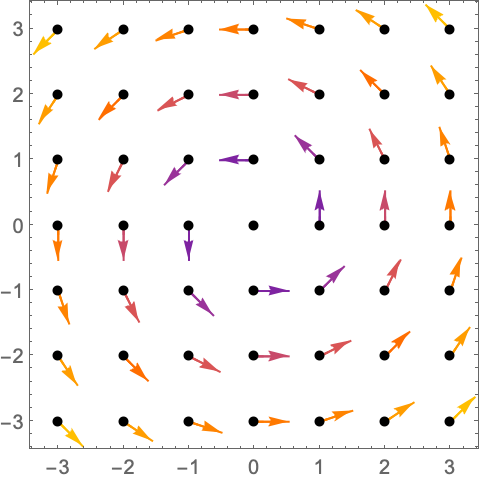
https://wolfram.com/xid/0n4i0sam2ea-2zlizz
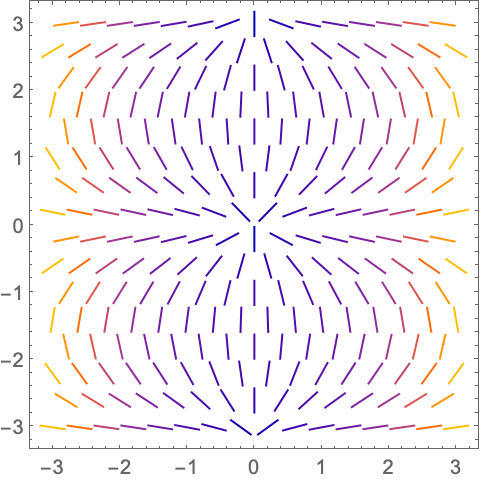
https://wolfram.com/xid/0n4i0sam2ea-fzve6t
https://wolfram.com/xid/0n4i0sam2ea-1zp5de
https://wolfram.com/xid/0n4i0sam2ea-oc0qdy
https://wolfram.com/xid/0n4i0sam2ea-v6aid7
https://wolfram.com/xid/0n4i0sam2ea-2kyz35
https://wolfram.com/xid/0n4i0sam2ea-cvzhyi

https://wolfram.com/xid/0n4i0sam2ea-n89e4w
https://wolfram.com/xid/0n4i0sam2ea-pblujj
https://wolfram.com/xid/0n4i0sam2ea-om0hcz
https://wolfram.com/xid/0n4i0sam2ea-fboha9
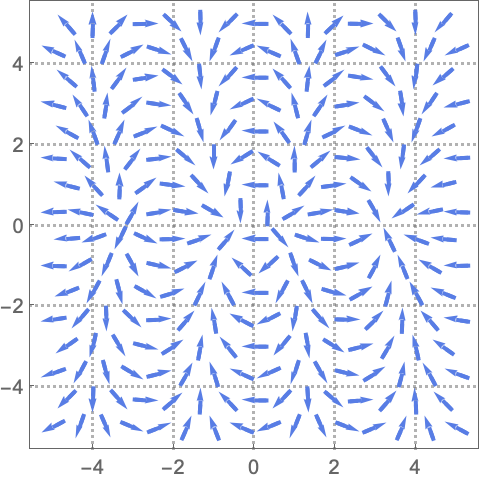
选项 (65)各选项的常用值和功能
ClippingStyle (4)
https://wolfram.com/xid/0n4i0sam2ea-dxfsnw
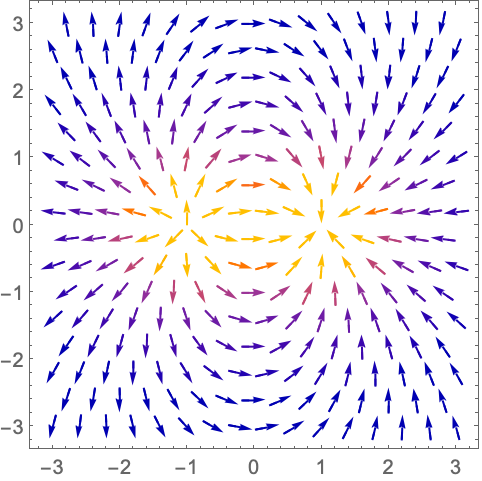
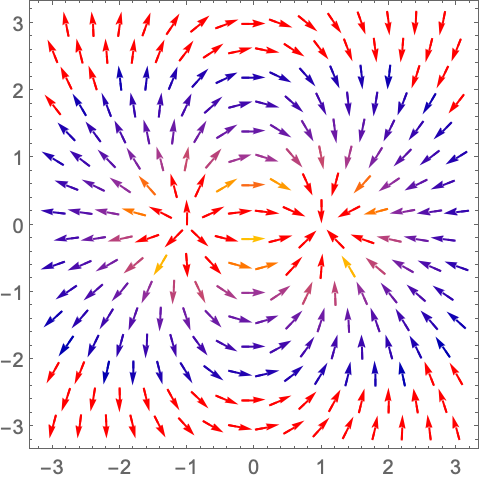
用 ClippingStyleNone 移除极短和极长的向量:
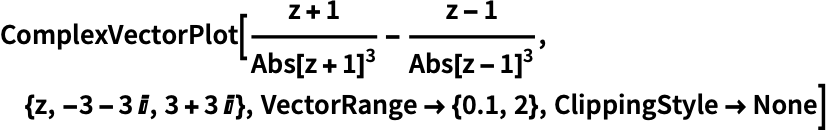
https://wolfram.com/xid/0n4i0sam2ea-f7s8c3
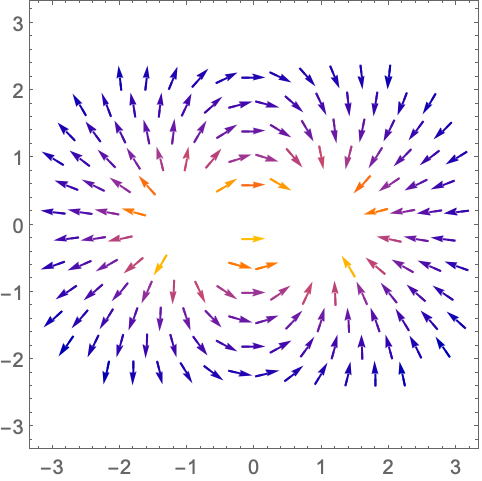
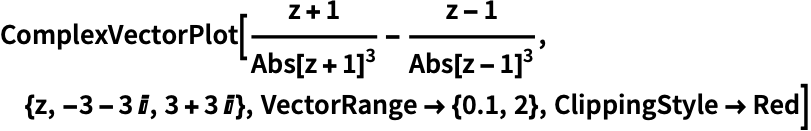
https://wolfram.com/xid/0n4i0sam2ea-edm9pg
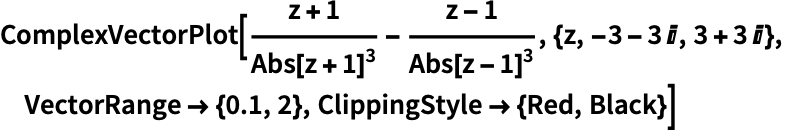
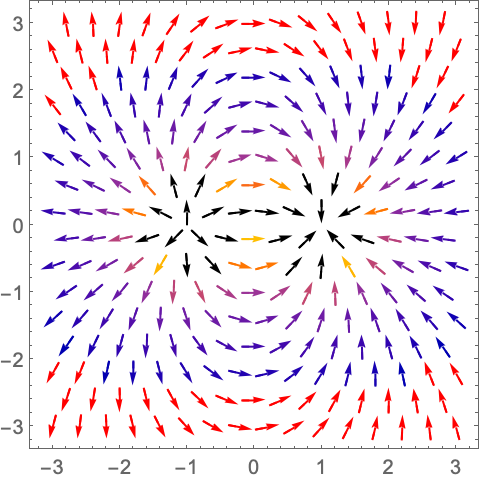
https://wolfram.com/xid/0n4i0sam2ea-b6iwnl
EvaluationMonitor (2)
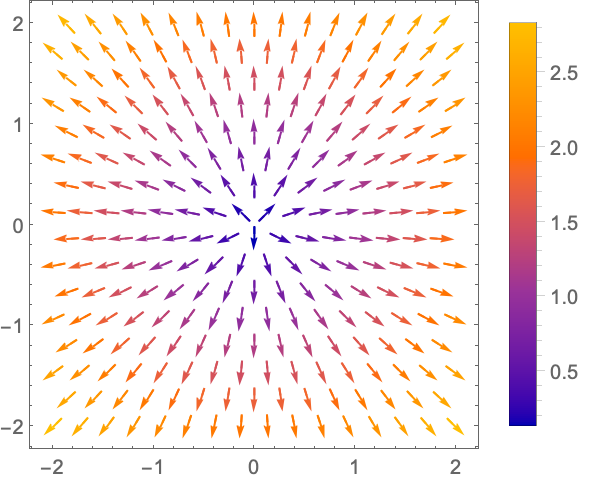
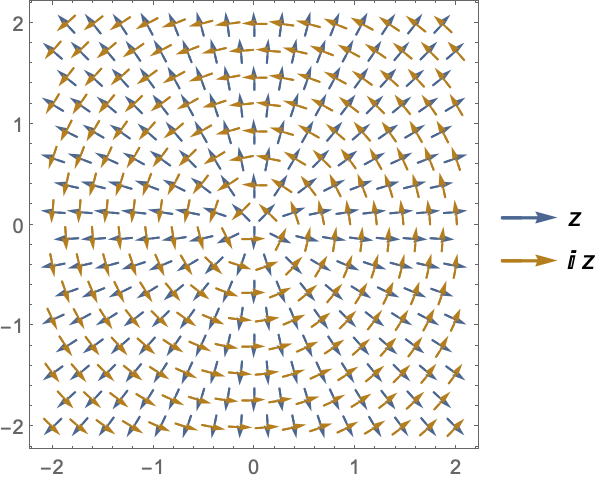
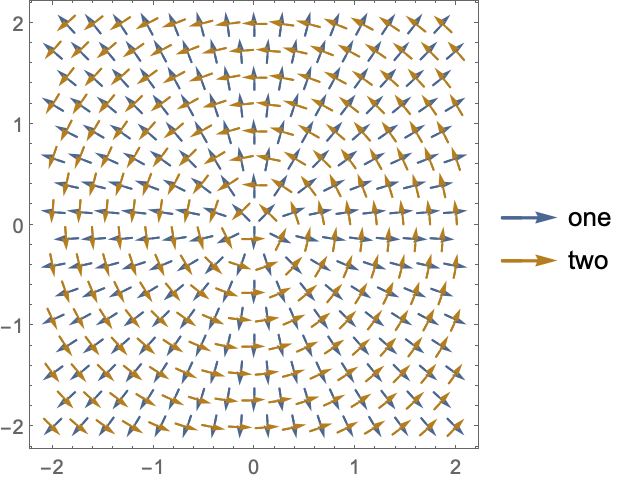
PlotLegends (5)
https://wolfram.com/xid/0n4i0sam2ea-js95u9
https://wolfram.com/xid/0n4i0sam2ea-ba8k3h
https://wolfram.com/xid/0n4i0sam2ea-n2fvi5
https://wolfram.com/xid/0n4i0sam2ea-cvx3dl
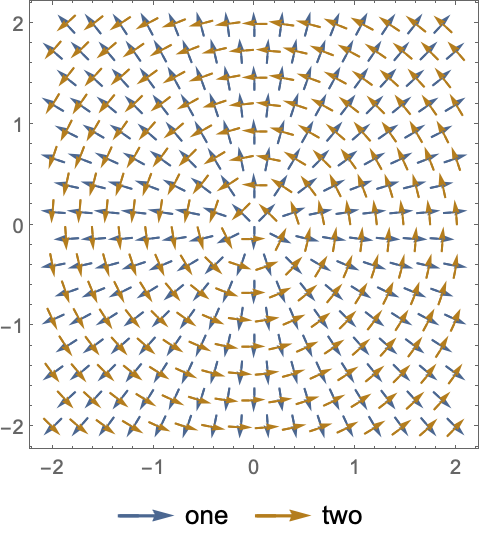
https://wolfram.com/xid/0n4i0sam2ea-m36w5m
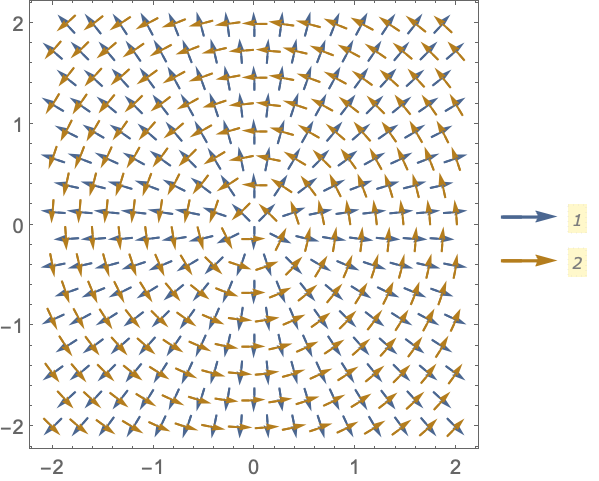
PlotRange (5)
https://wolfram.com/xid/0n4i0sam2ea-g6xoyw
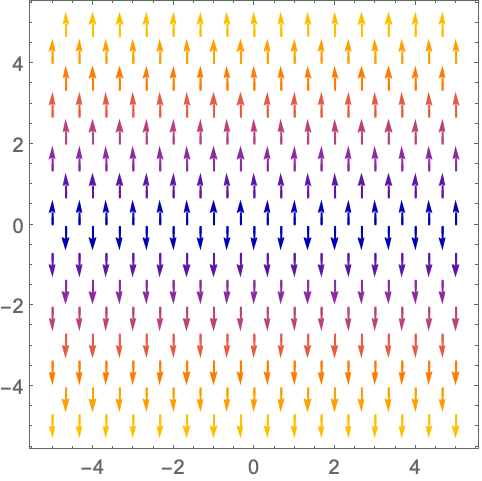
https://wolfram.com/xid/0n4i0sam2ea-5on0y
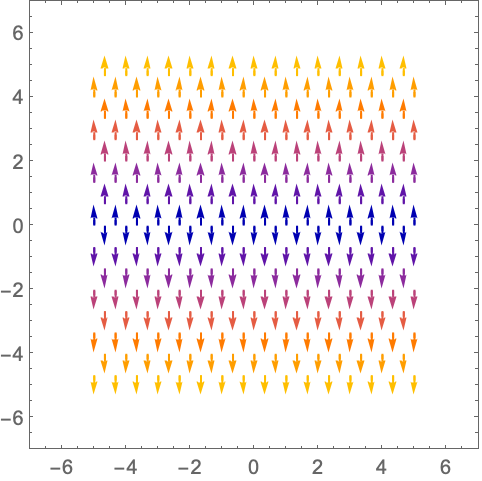
https://wolfram.com/xid/0n4i0sam2ea-i4n6y8
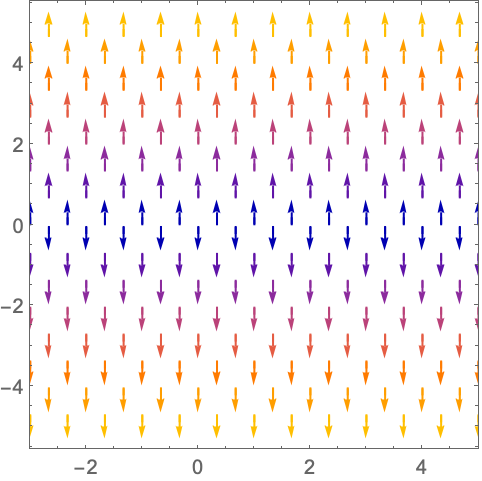
https://wolfram.com/xid/0n4i0sam2ea-xat4r
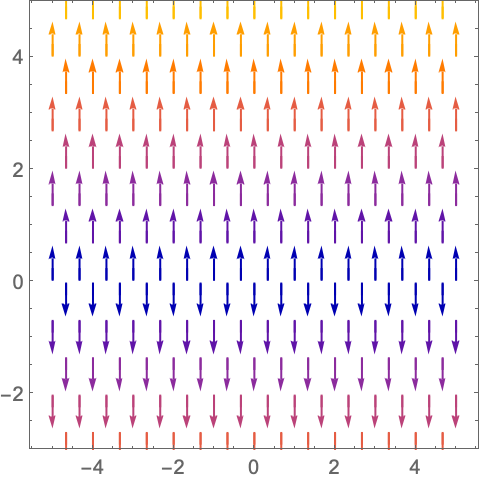
https://wolfram.com/xid/0n4i0sam2ea-f1lr1g
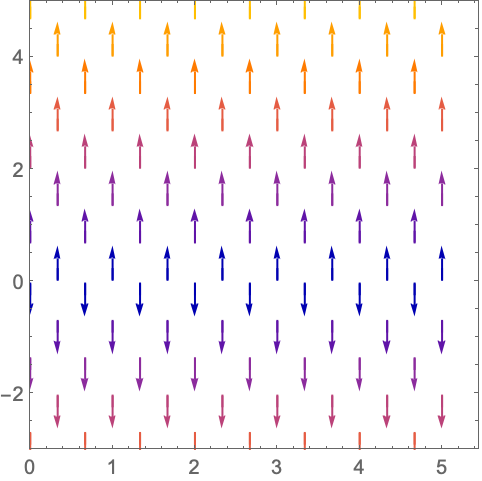
PlotTheme (2)
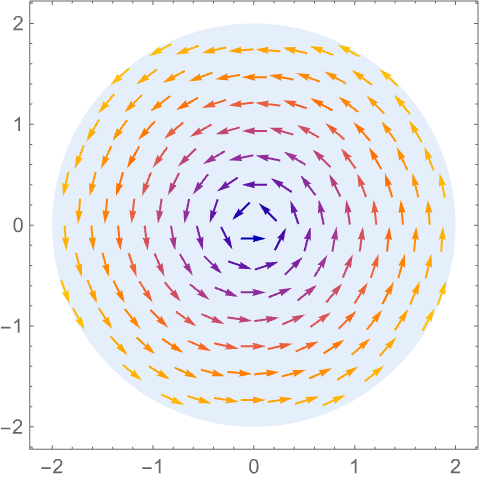
RegionBoundaryStyle (5)
https://wolfram.com/xid/0n4i0sam2ea-d6s6um
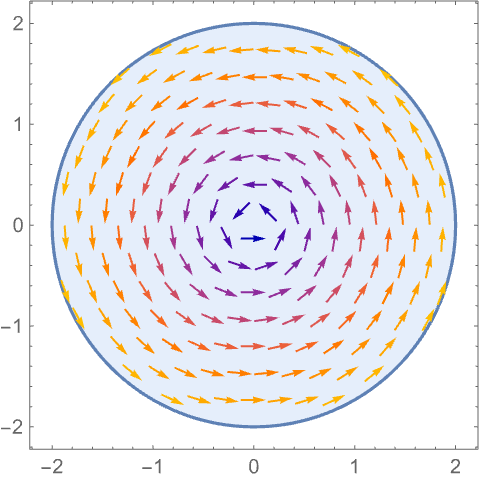
https://wolfram.com/xid/0n4i0sam2ea-7wf5ba
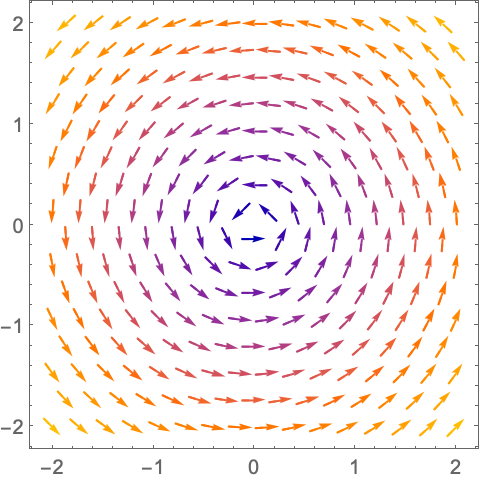
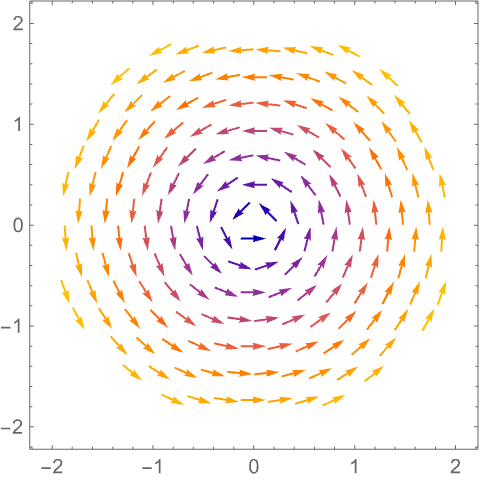
使用 None 不显示边界:
https://wolfram.com/xid/0n4i0sam2ea-d87zny
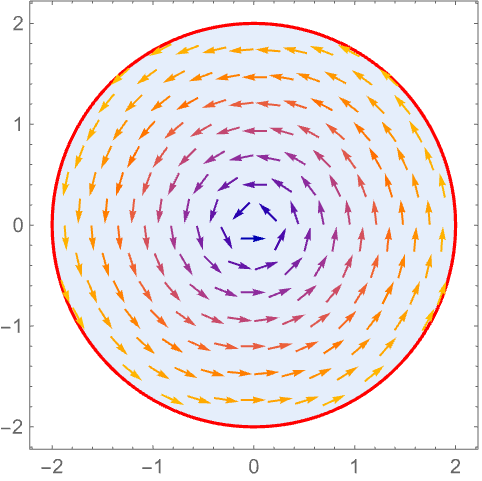
https://wolfram.com/xid/0n4i0sam2ea-gr12m6
https://wolfram.com/xid/0n4i0sam2ea-dd19je
https://wolfram.com/xid/0n4i0sam2ea-ozzhd4
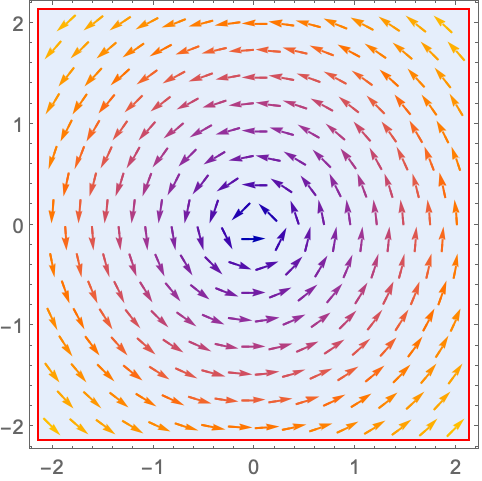
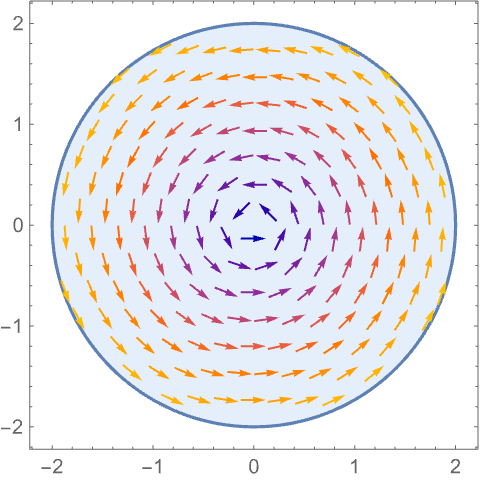
RegionFillingStyle (5)
https://wolfram.com/xid/0n4i0sam2ea-b1r4jl
https://wolfram.com/xid/0n4i0sam2ea-cxnsd5
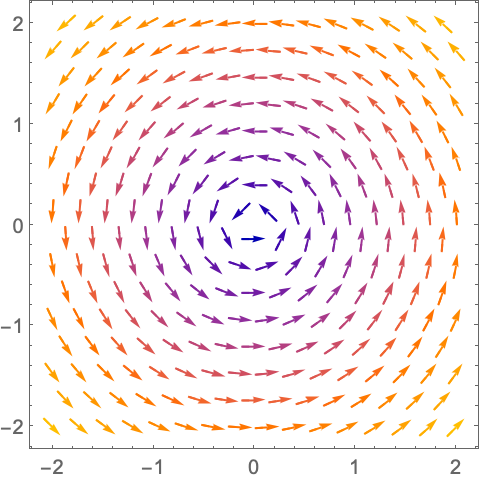
使用 None 不显示内部填充:
https://wolfram.com/xid/0n4i0sam2ea-clzxe7
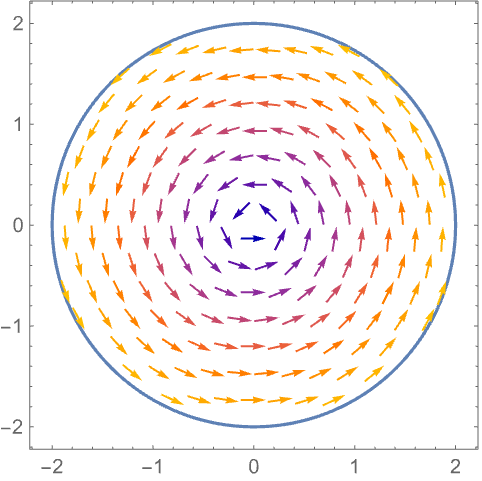
https://wolfram.com/xid/0n4i0sam2ea-f27m9u
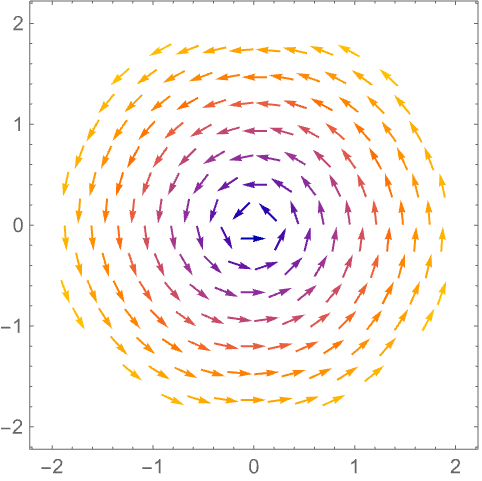
https://wolfram.com/xid/0n4i0sam2ea-uquau7
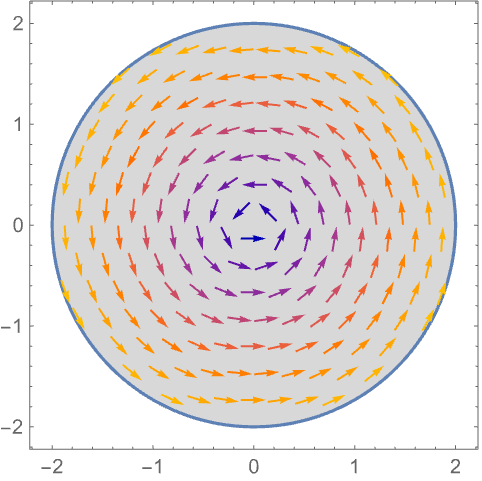
https://wolfram.com/xid/0n4i0sam2ea-f0shd2
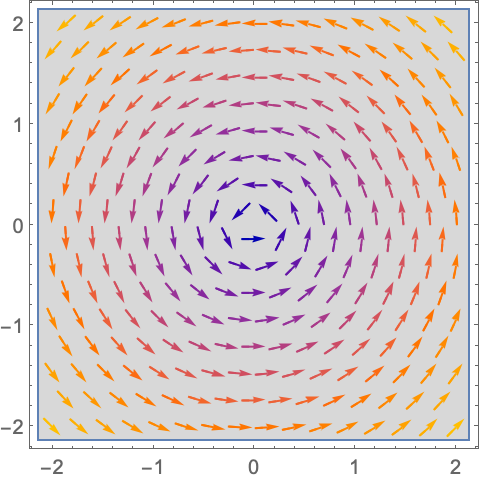
RegionFunction (2)
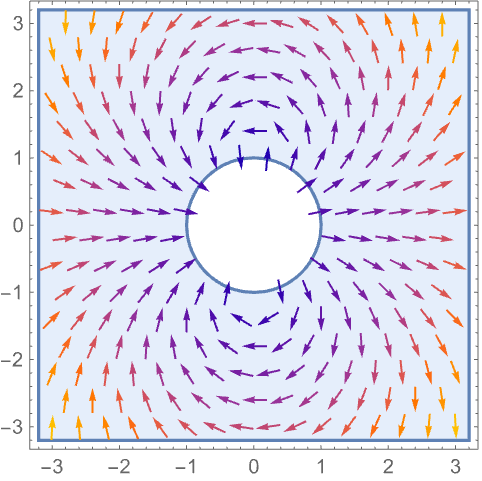
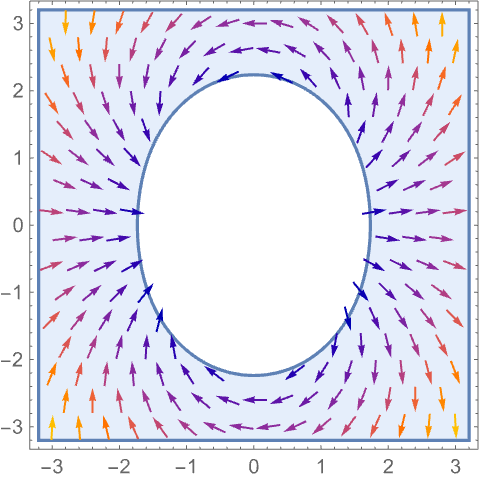
VectorAspectRatio (2)
VectorColorFunction (5)
https://wolfram.com/xid/0n4i0sam2ea-b7adpr
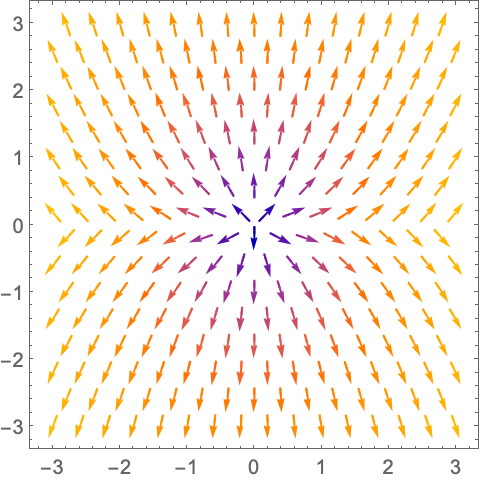
https://wolfram.com/xid/0n4i0sam2ea-cdiw5o
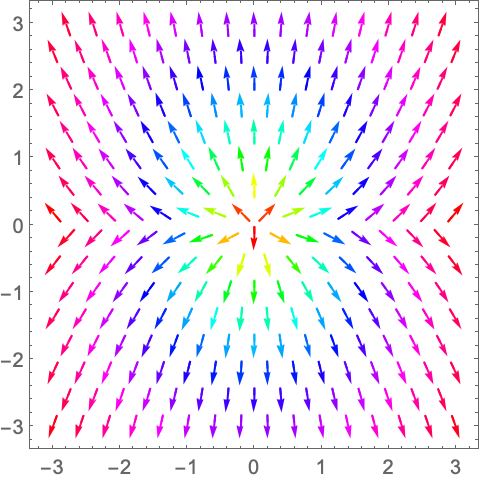
使用来自 ColorData 的已命名的颜色梯度:
https://wolfram.com/xid/0n4i0sam2ea-dsi8pl
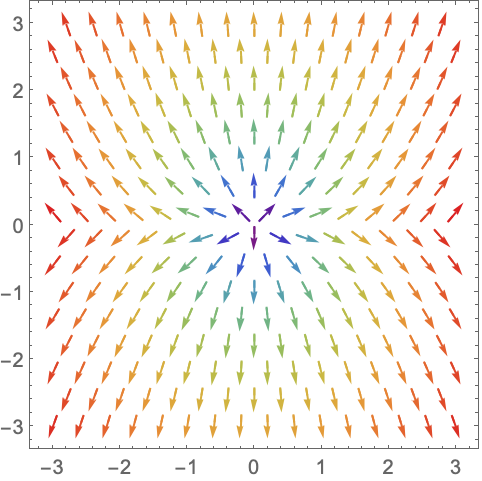
https://wolfram.com/xid/0n4i0sam2ea-bw7lma
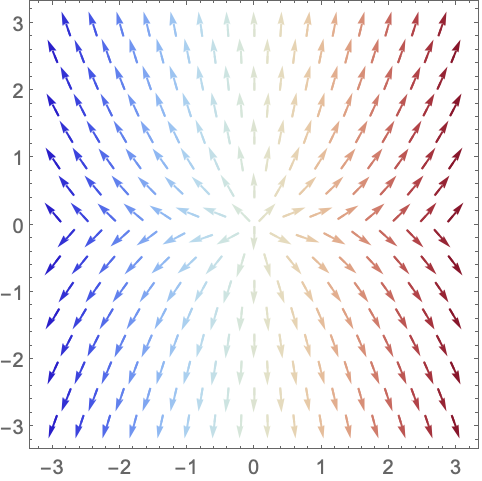
https://wolfram.com/xid/0n4i0sam2ea-lf15n
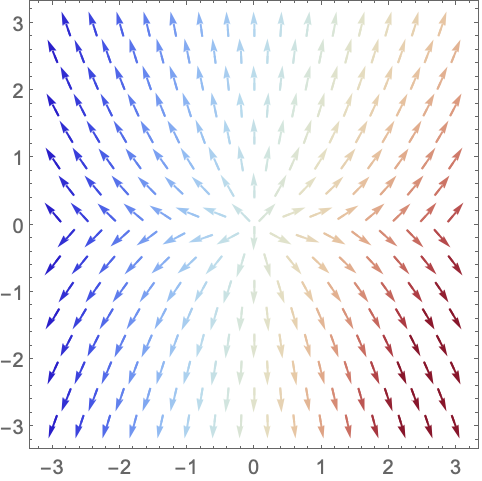
VectorColorFunctionScaling (2)
https://wolfram.com/xid/0n4i0sam2ea-c7h4ae
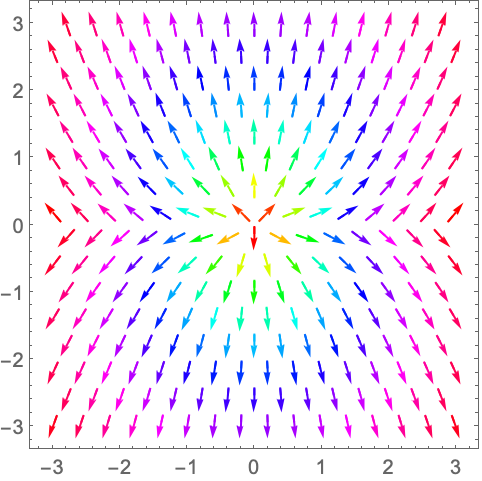
用 VectorColorFunctionScalingFalse 获取未经缩放的值:
https://wolfram.com/xid/0n4i0sam2ea-drzoi2
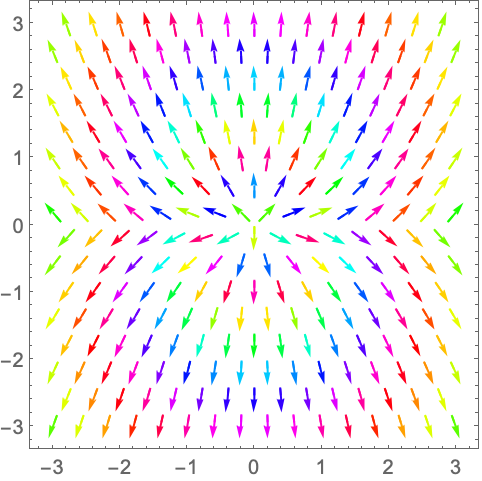
VectorMarkers (4)
https://wolfram.com/xid/0n4i0sam2ea-d31ee2
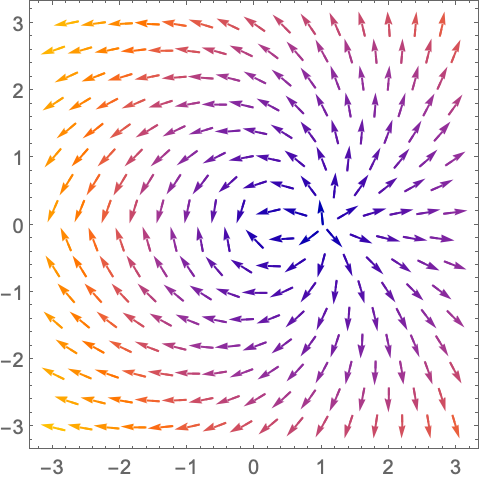

https://wolfram.com/xid/0n4i0sam2ea-kk973g
https://wolfram.com/xid/0n4i0sam2ea-et2q04
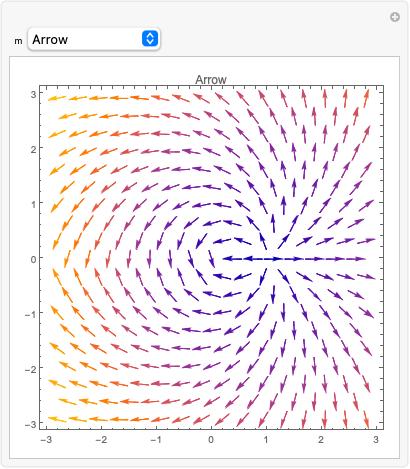
https://wolfram.com/xid/0n4i0sam2ea-i7fp68
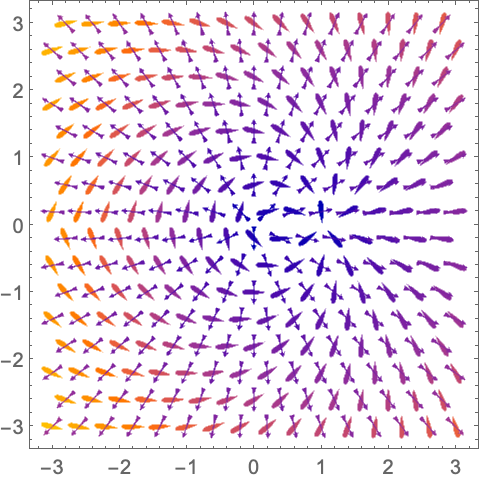
https://wolfram.com/xid/0n4i0sam2ea-dfllwr
https://wolfram.com/xid/0n4i0sam2ea-lfxai2
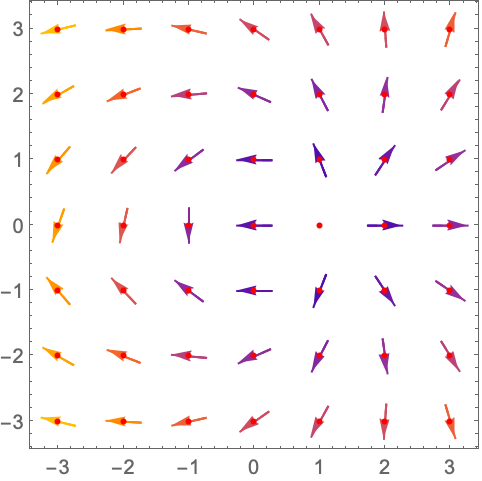

https://wolfram.com/xid/0n4i0sam2ea-opwap5
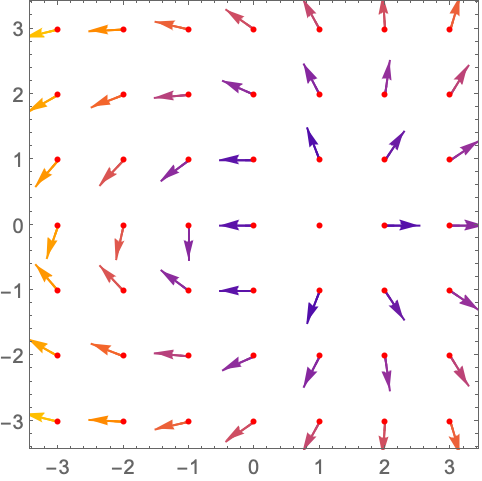

https://wolfram.com/xid/0n4i0sam2ea-iweszu
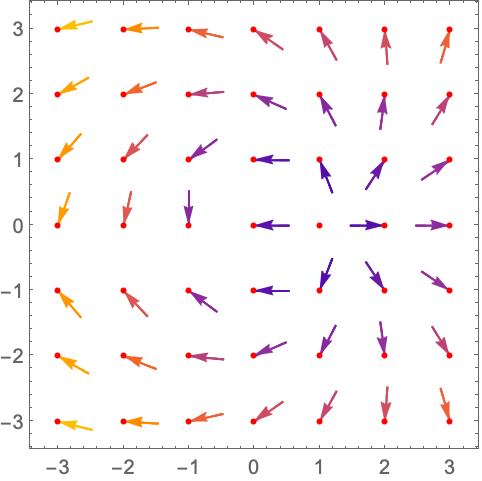
VectorPoints (5)
https://wolfram.com/xid/0n4i0sam2ea-bkxnrk
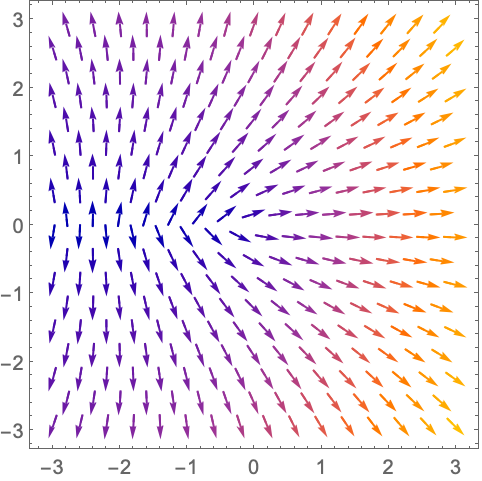
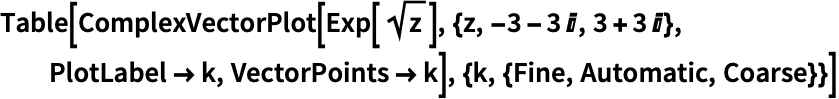
https://wolfram.com/xid/0n4i0sam2ea-dhad3u
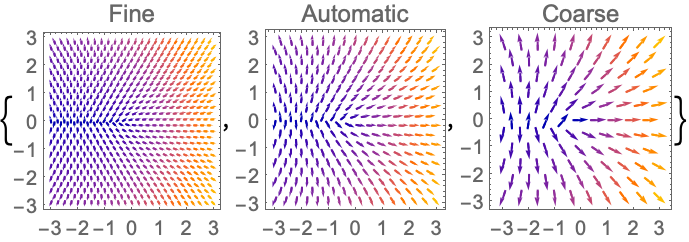
https://wolfram.com/xid/0n4i0sam2ea-lp1zg
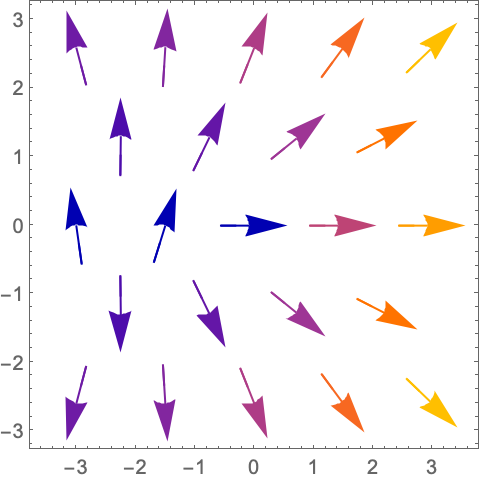
https://wolfram.com/xid/0n4i0sam2ea-e0q7cn
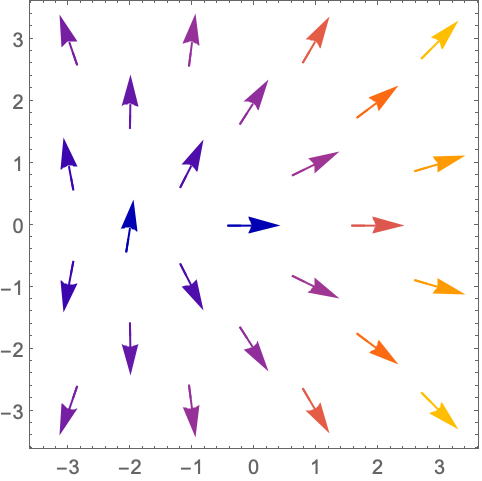
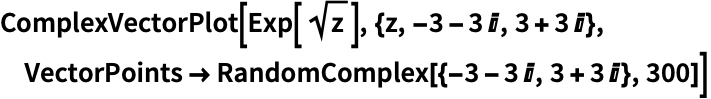
https://wolfram.com/xid/0n4i0sam2ea-fkgaai
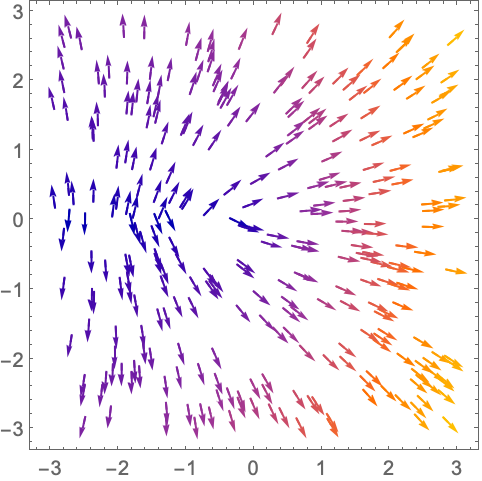
VectorRange (6)
https://wolfram.com/xid/0n4i0sam2ea-fdojbp
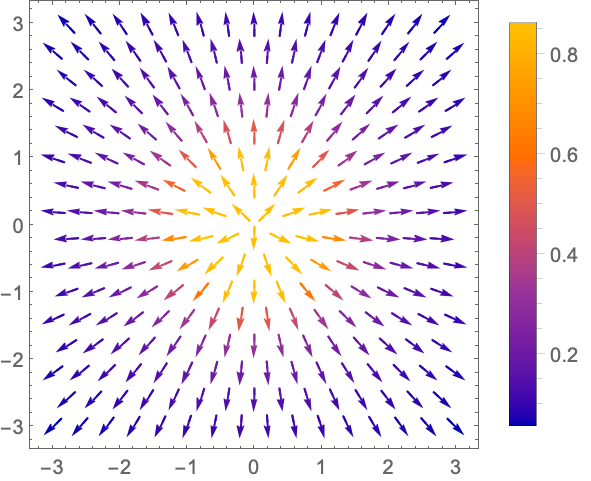
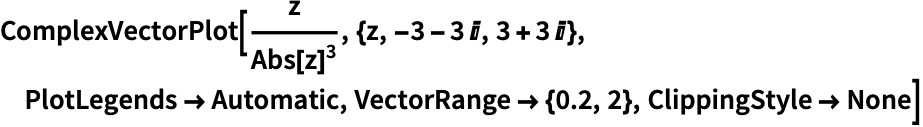
https://wolfram.com/xid/0n4i0sam2ea-m4l3r
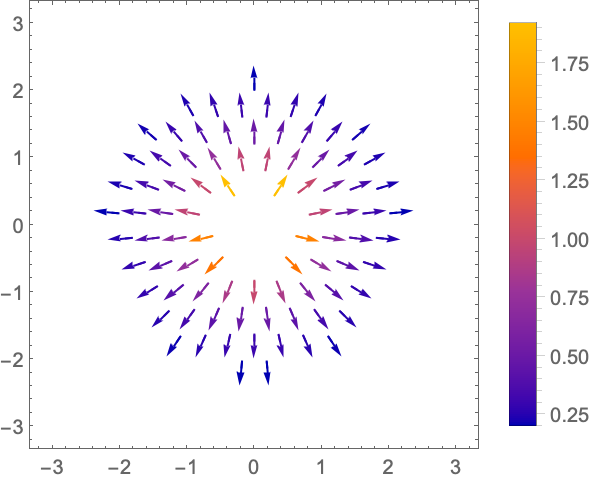
对箭头的长度进行缩放,绘制幅值在 0.2 到 2 之间的向量:
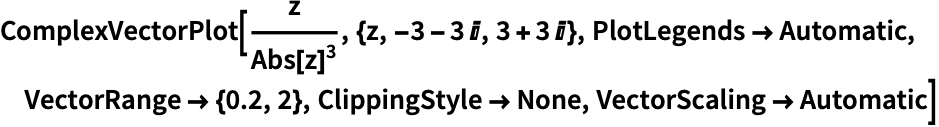
https://wolfram.com/xid/0n4i0sam2ea-gthzzm
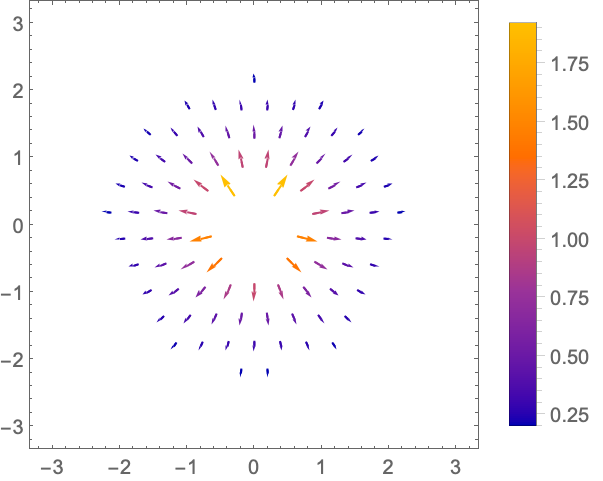
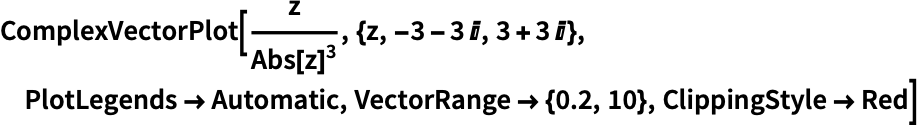
https://wolfram.com/xid/0n4i0sam2ea-y3wfh
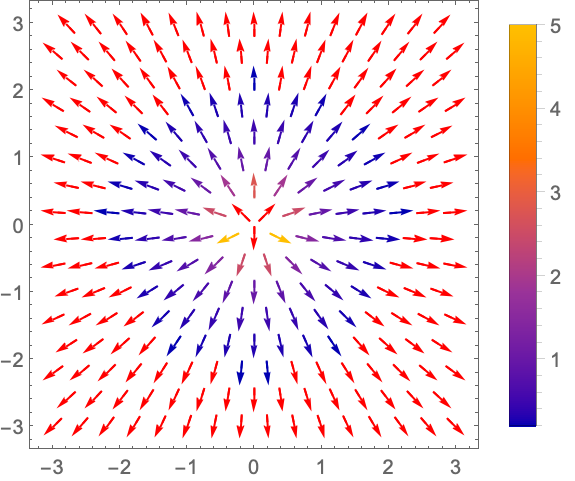
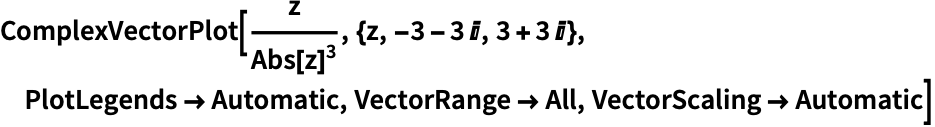
https://wolfram.com/xid/0n4i0sam2ea-g9h1vr
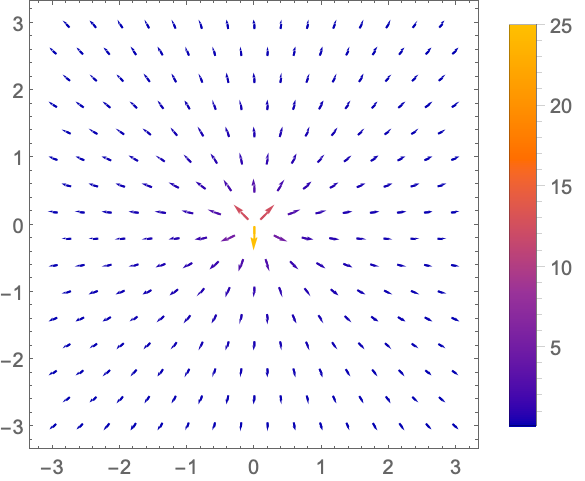

https://wolfram.com/xid/0n4i0sam2ea-fljz8c
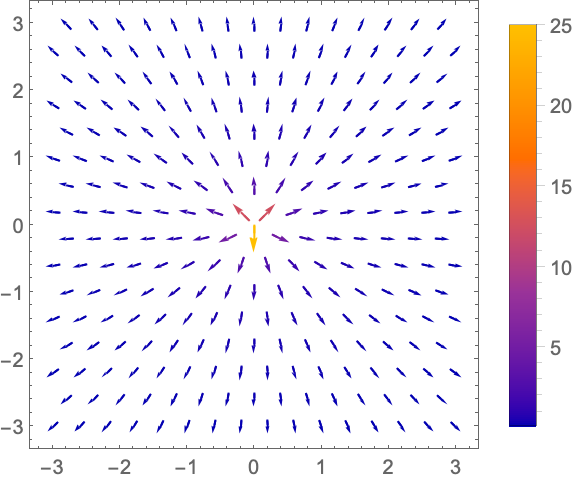
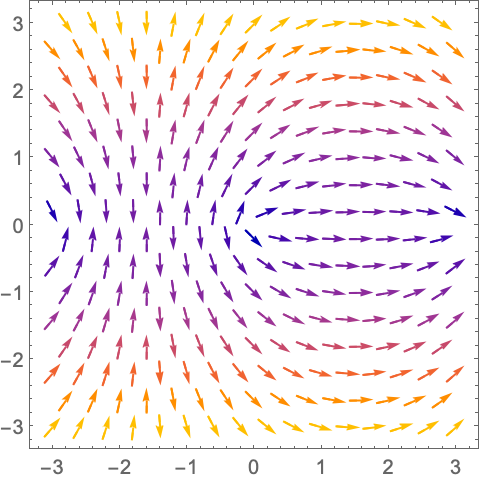
VectorScaling (2)
默认情况下,VectorScaling 被设为 None:
https://wolfram.com/xid/0n4i0sam2ea-ml02wa
https://wolfram.com/xid/0n4i0sam2ea-84w8x5
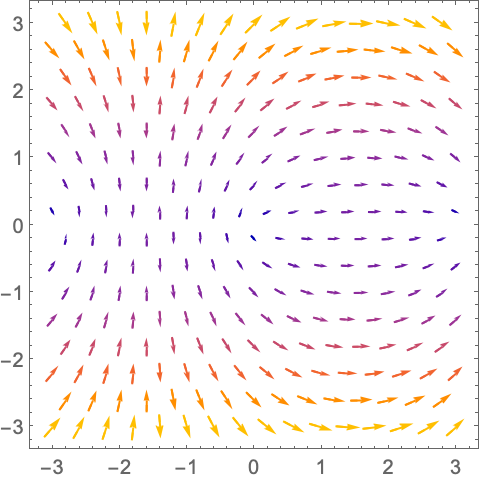
VectorSizes (2)
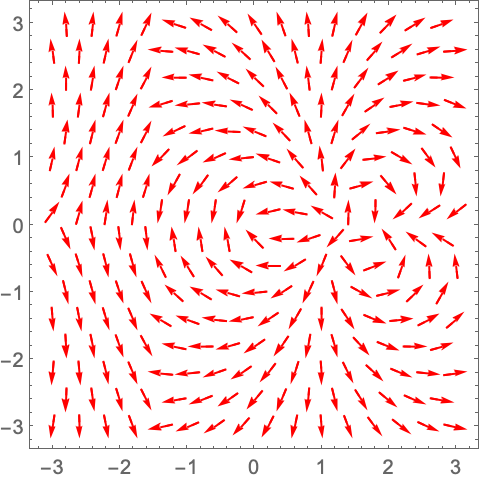
VectorStyle (6)
https://wolfram.com/xid/0n4i0sam2ea-hnrejz
https://wolfram.com/xid/0n4i0sam2ea-fqpqa1
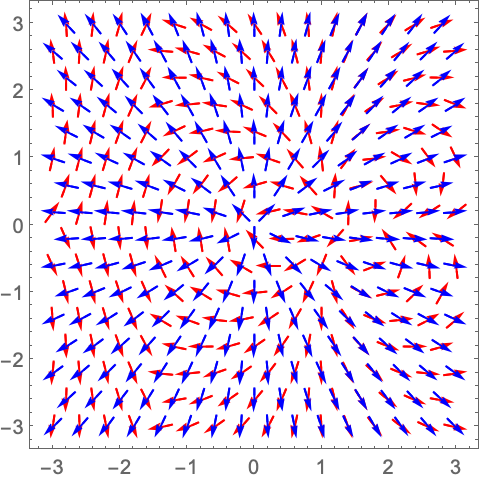
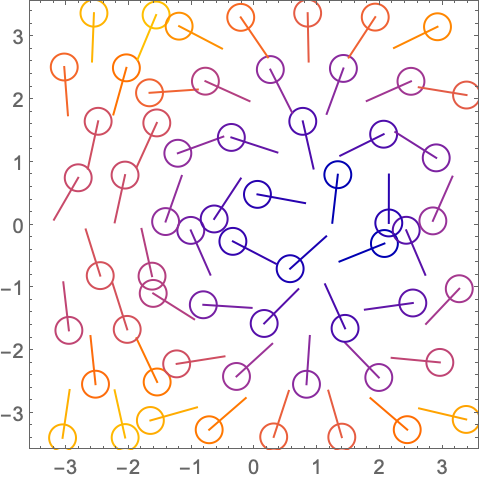
用 Arrowheads 明确指定箭头的样式:
https://wolfram.com/xid/0n4i0sam2ea-bjd7u

https://wolfram.com/xid/0n4i0sam2ea-f4aho
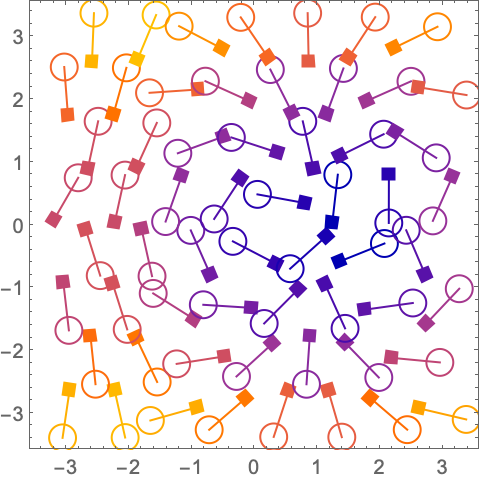
对于没有 Arrowheads 的图像指令,按向量的 scale 进行缩放:
https://wolfram.com/xid/0n4i0sam2ea-dmphsg
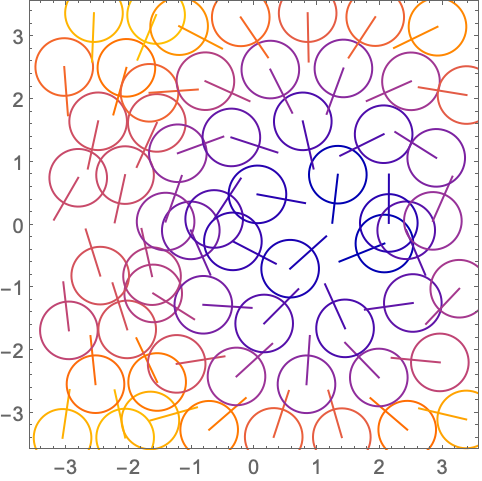
用 VectorScaling 选项改变缩放方式:
https://wolfram.com/xid/0n4i0sam2ea-i0vjuu
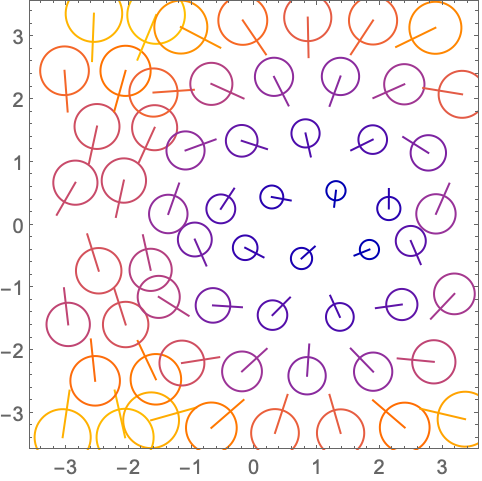
应用 (7)用该函数可以解决的问题范例
https://wolfram.com/xid/0n4i0sam2ea-de7yae
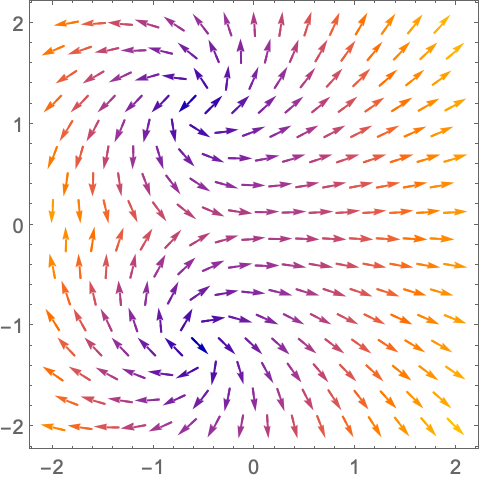
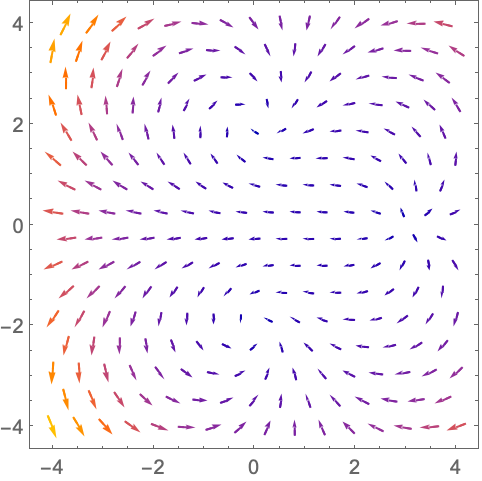
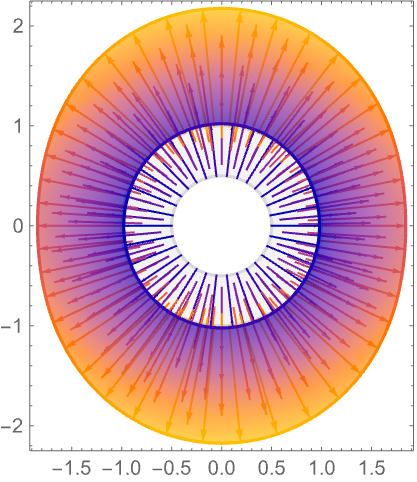
向量的长度随 Abs[f] 的增大而增大,方向则由 Arg[f] 决定:
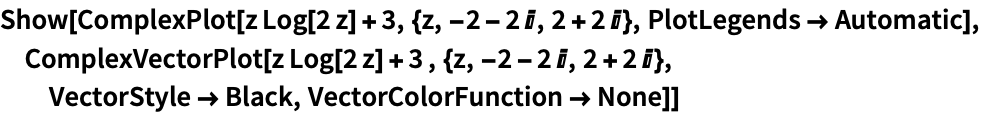
https://wolfram.com/xid/0n4i0sam2ea-c2tmq2
https://wolfram.com/xid/0n4i0sam2ea-lm37cf
https://wolfram.com/xid/0n4i0sam2ea-bftb2b
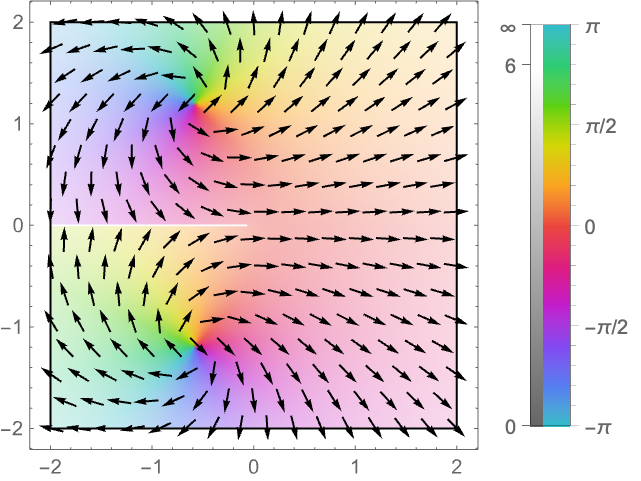
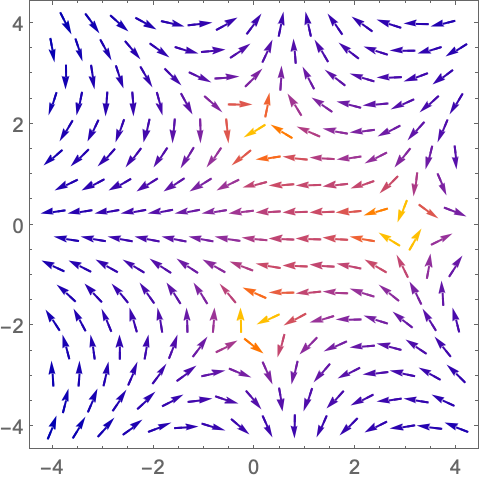
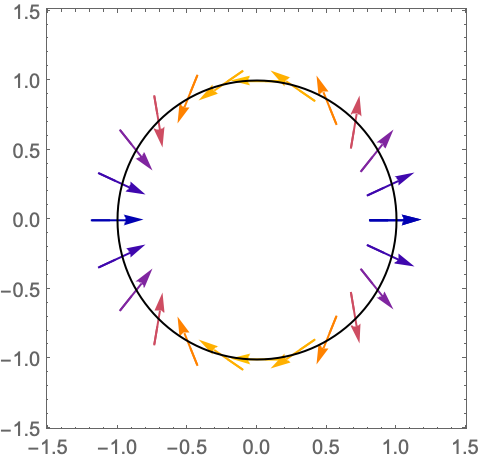
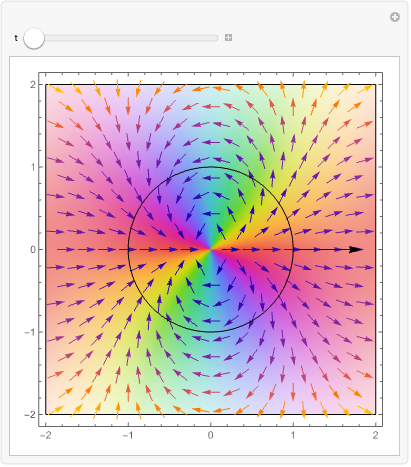
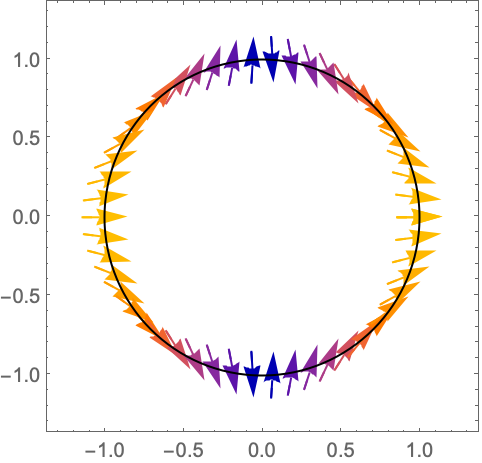
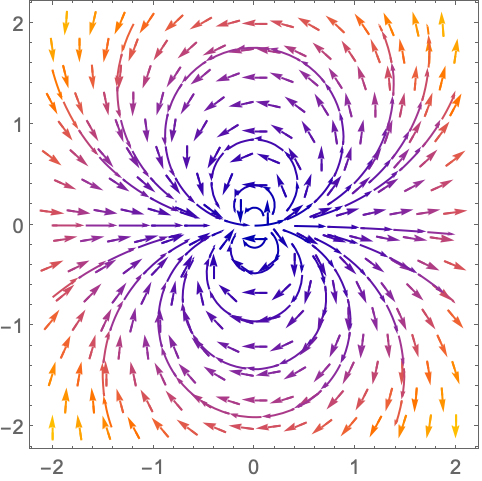
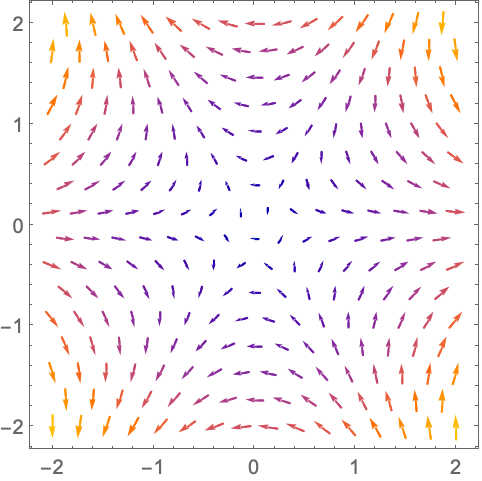
场向量沿单位圆环绕函数 ![]() 在原点处的零点两次,这意味着
在原点处的零点两次,这意味着 ![]() 在原点具有双重零点:
在原点具有双重零点:
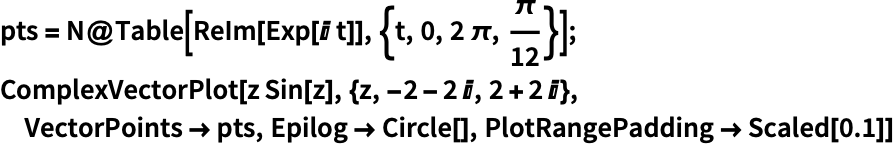
https://wolfram.com/xid/0n4i0sam2ea-gqfooa
https://wolfram.com/xid/0n4i0sam2ea-lftmd9

https://wolfram.com/xid/0n4i0sam2ea-dz4b1
https://wolfram.com/xid/0n4i0sam2ea-fb86wg

https://wolfram.com/xid/0n4i0sam2ea-g66tey
https://wolfram.com/xid/0n4i0sam2ea-fhs1yu
https://wolfram.com/xid/0n4i0sam2ea-t15cu
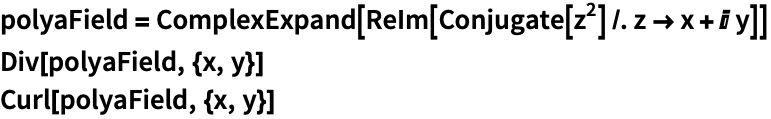
https://wolfram.com/xid/0n4i0sam2ea-7ibeo

https://wolfram.com/xid/0n4i0sam2ea-f2wpwi
https://wolfram.com/xid/0n4i0sam2ea-f0vzlx
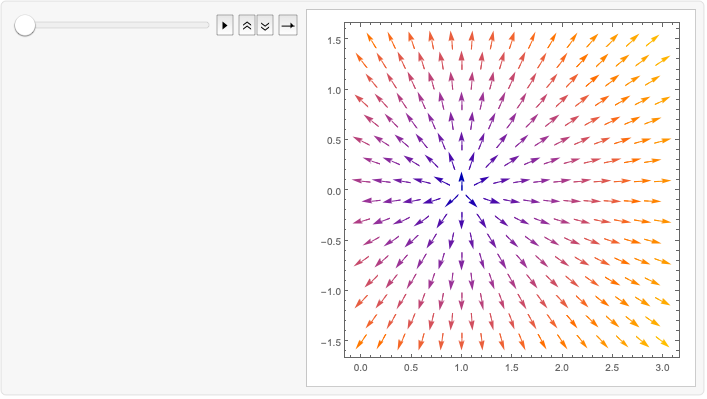
属性和关系 (15)函数的属性及与其他函数的关联
ComplexVectorPlot 是 VectorPlot 的特例:
https://wolfram.com/xid/0n4i0sam2ea-cb87oq
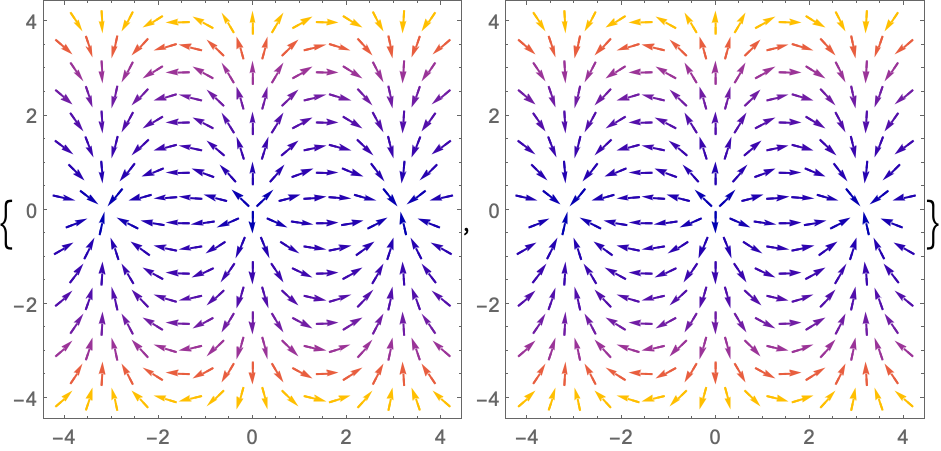
ComplexStreamPlot 将复数绘制为流线:
https://wolfram.com/xid/0n4i0sam2ea-7studa
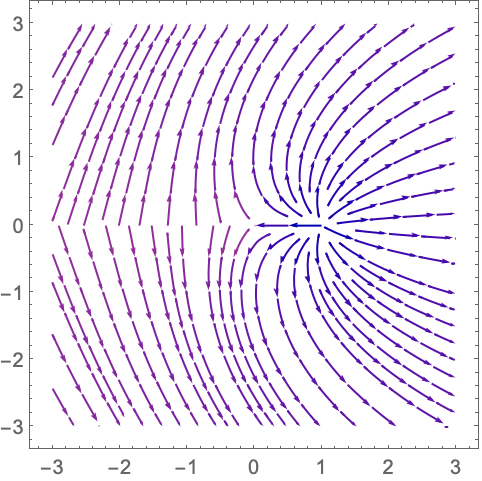
ComplexStreamPlot 是 StreamPlot 的特殊情况:
https://wolfram.com/xid/0n4i0sam2ea-c53rr6
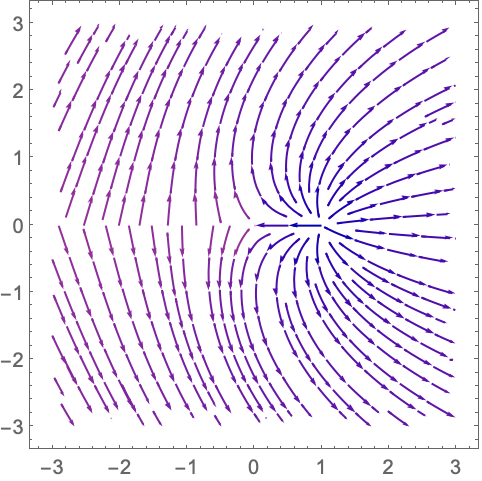
使用 VectorDisplacementPlot 可视化指定区域内复函数的效果:
https://wolfram.com/xid/0n4i0sam2ea-kx8huh
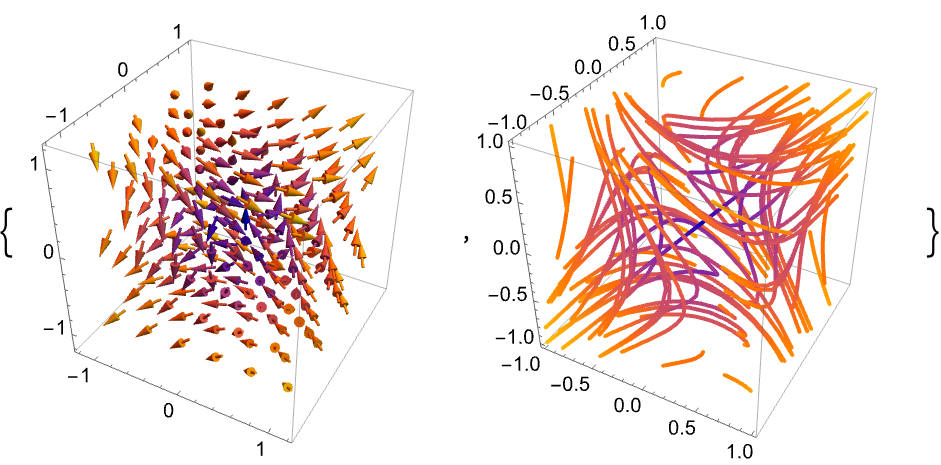
用 VectorPlot3D 和 StreamPlot3D 可视化三维向量场:
https://wolfram.com/xid/0n4i0sam2ea-h3ykri
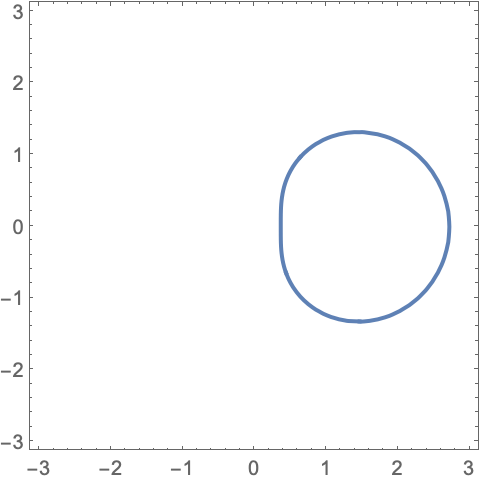
ComplexContourPlot 绘制复平面上的曲线:
https://wolfram.com/xid/0n4i0sam2ea-pesif0
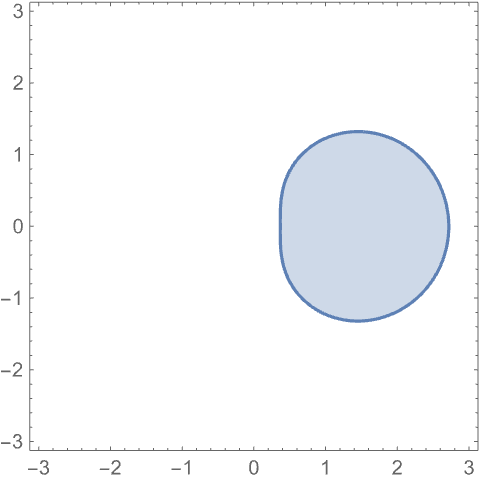
ComplexRegionPlot 绘制复平面上的区域:
https://wolfram.com/xid/0n4i0sam2ea-ko83ut
ComplexPlot 用颜色显示函数的辐角和幅值:
https://wolfram.com/xid/0n4i0sam2ea-e28611
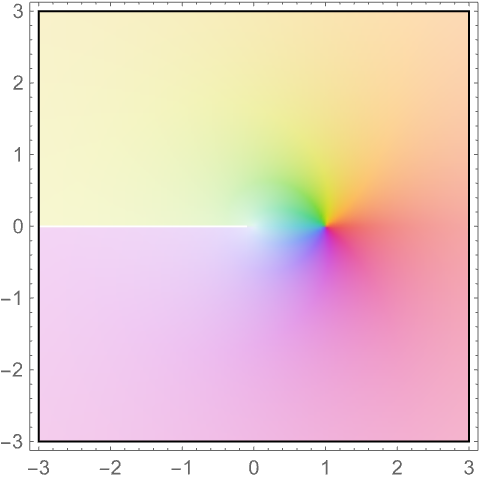
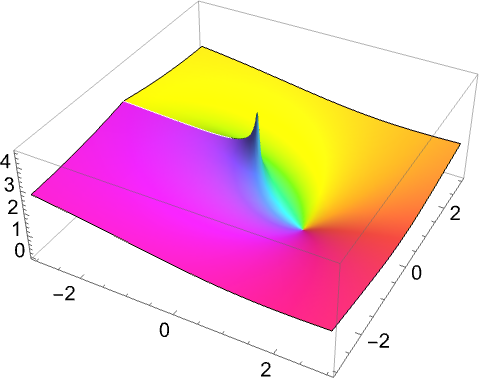
通过 ComplexPlot3D 用 ![]() 轴显示幅值:
轴显示幅值:
https://wolfram.com/xid/0n4i0sam2ea-vgce1e
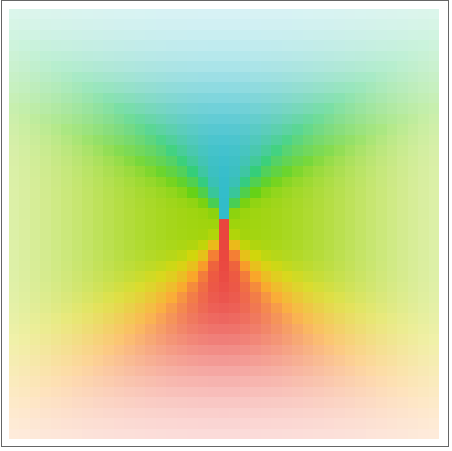
用 ComplexArrayPlot 绘制复数数组:
https://wolfram.com/xid/0n4i0sam2ea-p6xumo
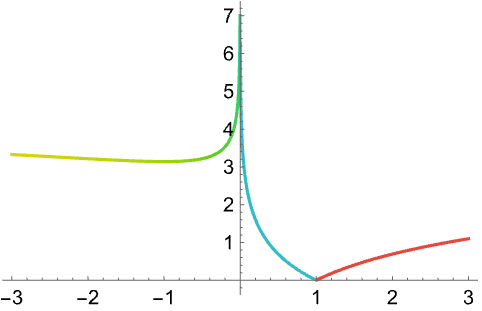
用 ReImPlot 和 AbsArgPlot 在实平面上绘制复数:
https://wolfram.com/xid/0n4i0sam2ea-0vi62l
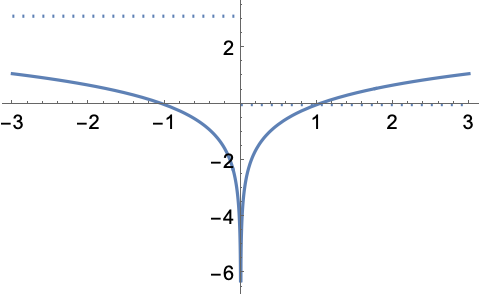
https://wolfram.com/xid/0n4i0sam2ea-mqa938
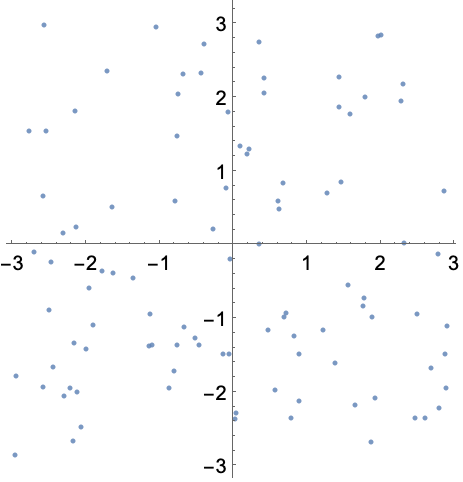
用 ComplexListPlot 显示复数在平面上的位置:
https://wolfram.com/xid/0n4i0sam2ea-wyd4bn
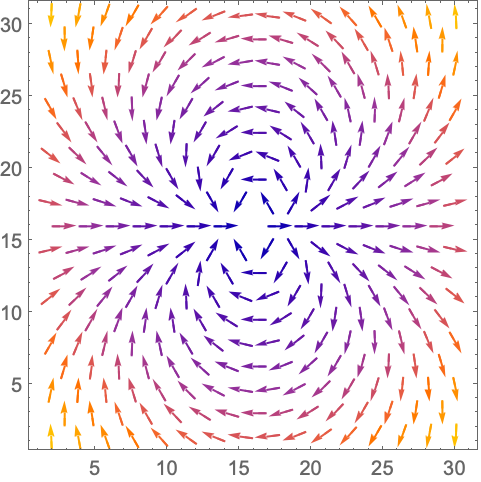
使用 ListVectorPlot 进行数据绘制:
https://wolfram.com/xid/0n4i0sam2ea-czc8d0
https://wolfram.com/xid/0n4i0sam2ea-bzenb8
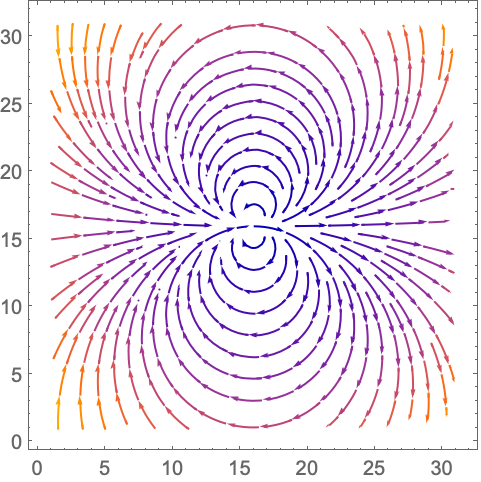
使用 ListStreamPlot 绘制流线图而非向量:
https://wolfram.com/xid/0n4i0sam2ea-efbl3z
使用 VectorDensityPlot 添加标量场的密度图:
https://wolfram.com/xid/0n4i0sam2ea-gljrl7
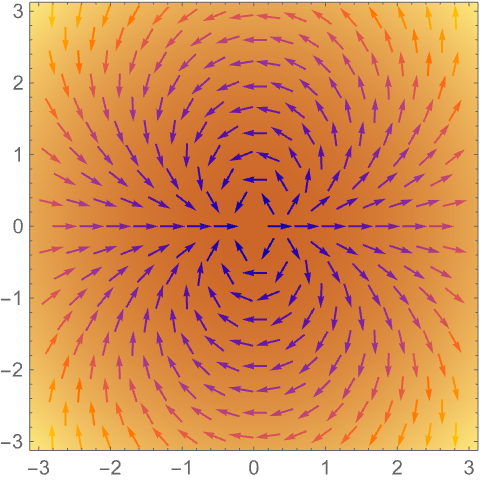
函数 StreamDensityPlot 可用于流线图而非向量:
https://wolfram.com/xid/0n4i0sam2ea-kxyms1
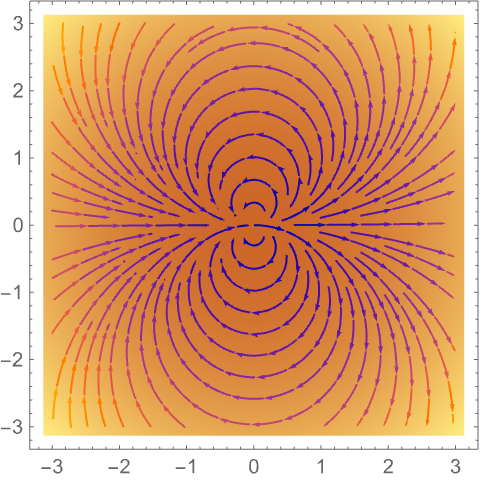
使用 ListVectorDensityPlot 生成基于数据的标量场的密度图:
https://wolfram.com/xid/0n4i0sam2ea-2fsjy
https://wolfram.com/xid/0n4i0sam2ea-b5me24
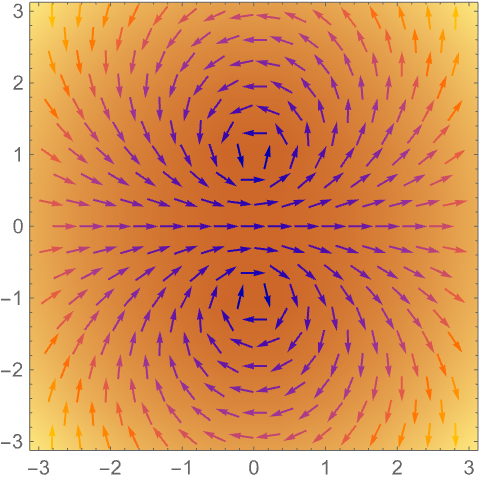
使用 ListStreamDensityPlot 绘制流线图而非向量:
https://wolfram.com/xid/0n4i0sam2ea-eootc
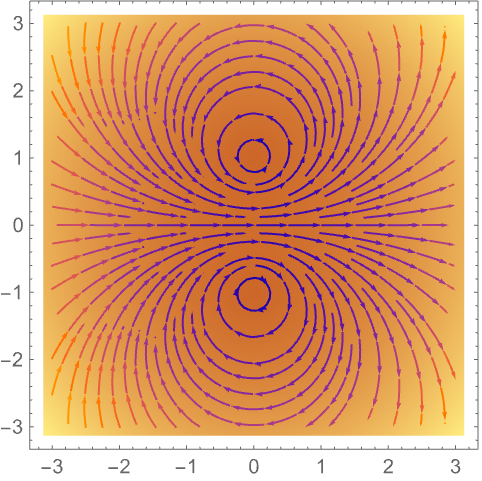
使用 LineIntegralConvolutionPlot 绘制向量场的线积分卷积:
https://wolfram.com/xid/0n4i0sam2ea-c9d537
Wolfram Research (2020),ComplexVectorPlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ComplexVectorPlot.html.文本
Wolfram Research (2020),ComplexVectorPlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ComplexVectorPlot.html.
Wolfram Research (2020),ComplexVectorPlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ComplexVectorPlot.html.CMS
Wolfram 语言. 2020. "ComplexVectorPlot." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ComplexVectorPlot.html.
Wolfram 语言. 2020. "ComplexVectorPlot." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ComplexVectorPlot.html.APA
Wolfram 语言. (2020). ComplexVectorPlot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ComplexVectorPlot.html 年
Wolfram 语言. (2020). ComplexVectorPlot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ComplexVectorPlot.html 年BibTeX
@misc{reference.wolfram_2025_complexvectorplot, author="Wolfram Research", title="{ComplexVectorPlot}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/ComplexVectorPlot.html}", note=[Accessed: 22-June-2025
]}BibLaTeX
@online{reference.wolfram_2025_complexvectorplot, organization={Wolfram Research}, title={ComplexVectorPlot}, year={2020}, url={https://reference.wolfram.com/language/ref/ComplexVectorPlot.html}, note=[Accessed: 22-June-2025
]}