DiscretizeGraphics
2Dあるいは3Dのグラフィックス g をMeshRegionに離散化する.
DiscretizeGraphics[g,patt]
g 中のパターン patt にマッチする要素のみを離散化する.
詳細とオプション




- DiscretizeGraphicsは,グラフィックスを,MeshRegionで使われる区分線形セルの不連続な和集合に離散化する.
- グラフィックス g は,Graphics,Graphics3Dあるいは個別のグラフィックスプリミティブでよい.
- DiscretizeGraphicsは,事実上,GraphicsおよびGraphics3D中の複数のプリミティブを和集合の操作として扱う.
- g が有界の区分線形プリミティブのみを含む場合は,離散化は厳密である.それ以外の場合は近似的である.
- 次は,厳密に表すことができるGraphics中の有界の区分的線形プリミティブである.
-
Point[…] 点 (0D) Line[…] 線 (1D) Triangle[…] 塗り潰された三角形 (2D) Polygon[…] 塗り潰された多角形 (2D) Rectangle[…] 塗り潰された長方形 (2D) Parallelogram[…] 塗り潰された平行四辺形 (0D,1Dあるいは2D) Simplex[…] 単体 (0D,1Dあるいは2D) - これらに加え,SSSTriangle,SASTriangle,ASATriangle,AASTriangleも評価するとTriangleになり,厳密に表すことができる.
- 次は,有限範囲のみを表すことができるGraphics中の非有界の区分線形プリミティブである.
-
HalfLine[…] 半線あるいは放射線 (1D) InfiniteLine[…] 無限線 (1D) HalfPlane[…] 半空間 (2D) ConicHullRegion[…] 線形円錐 (0D,1Dあるいは2D) - 次は,近似的にのみ表すことができるGraphicsの非線形プリミティブである.
-
Circle[…] 円,楕円,扇形(1D) Disk[…] 円板,塗り潰された楕円,扇形(2D) BezierCurve[…] ベジエスプライン曲線(1D) BSplineCurve[…] Bスプライン曲線(1D) JoinedCurve[…] 結合された曲線分(1D) FilledCurve[…] 塗り潰された閉じた曲線(2D) - 加えて,Circumsphereを評価するとSphereになり,近似的に表すことができる.
- 次は,厳密に表すことができるGraphics3Dの有界の区分線形プリミティブである.
-
Point[…] 点 (0D) Line[…] 線 (1D) Triangle[…] 塗り潰された三角形 (2D) Polygon[…] 塗り潰された多角形 (2D) Cuboid[…] 塗り潰された直方体 (3D) Parallelepiped[…] 塗り潰された平行六面体 (0D,1D,2D,あるいは3D) Tetrahedron[…] 塗り潰された四面体 (3D) Hexahedron[…] 塗り潰された六面体 (3D) Pyramid[…] 塗り潰された角錐 (3D) Prism[…] 塗り潰された角柱 (3D) Simplex[…] 単体 (0D,1D,2D,あるいは3D) - 次は,有限範囲のみを表すことができるGraphics3Dの非有界の区分線形プリミティブである.
-
HalfLine[…] 半直線あるいは放射線 (1D) InfiniteLine[…] 無限線 (1D) HalfPlane[…] 1方向に有界である平面 (2D) InfinitePlane[…] 無限平面 (3D) ConicHullRegion[…] 線形円錐 (0D,1D,2D,あるいは3D) - 次は,近似的にのみ表すことができるGraphics3Dの非線形プリミティブである.
-
BezierCurve[…] ベジエ曲線 (1D) BSplineCurve[…] Bスプライン曲線 (1D) JoinedCurve[…] 結合曲線分 (1D) BSplineSurface[…] Bスプライン曲面 (2D) Sphere[…] 球 (2D) Ball[…] 球体あるいは塗り潰された球 (3D) Ellipsoid[…] 塗り潰された楕円体 (3D) Cylinder[…] 塗り潰された円柱 (3D) Cone[…] 塗り潰された円錐 (3D) - 加えて,Circumsphereを評価するとSphereになるので,近似的に表すことができる.
- DiscretizeGraphicsには,MeshRegionと同じオプションに以下の追加・変更を加えたものが使える.
-
AccuracyGoal Automatic 目標確度 MaxCellMeasure Automatic 最大セル測度 MeshQualityGoal Automatic メッシュセルの品質目標 Method Automatic 使用するメソッド MeshRefinementFunction None メッシュをさらに分割する必要がある場合にTrueを返す関数 PlotRange Automatic 含める範囲 PerformanceGoal $PerformanceGoal スピードあるいは品質を考慮するかどうか PrecisionGoal Automatic 目標精度 - AccuracyGoal->a およびPrecisionGoal->p のときは,領域 reg あるいは離散化された領域 dreg とRegionSymmetricDifference[reg,dreg]の任意の点の間の距離を
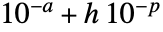 未満に保とうと試みられる.ただし,
未満に保とうと試みられる.ただし,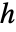 はプロット範囲の対角線の長さである.
はプロット範囲の対角線の長さである.
例題
すべて開くすべて閉じる例 (2)
スコープ (17)
Graphics (9)
Circleを含む2Dの特殊な領域を離散化する:
Point,Line,Polygonを含むGraphicsComplexのGraphicsを離散化する:
Rectangle,Circle,Diskを含むGraphicsComplexのGraphicsを離散化する:
すべての(All)プリミティブを離散化する:
有界の区分線形Graphicsプリミティブは,厳密に表すことができる:
非有界の区分線形Graphicsプリミティブは,有限範囲でのみ表すことができる:
非線形Graphicsプリミティブは近似的にしか表すことができない:
GraphicsComplexを含むグラフィックス:
MaxCellMeasureを使って離散化レベルを制御する:
Graphics3D (8)
Coneを含む,3Dの特別な領域を離散化する:
Point,Line,Polygonを含むGraphicsComplexのGraphics3Dを離散化する:
複数のプリミティブが和集合として解釈されるGraphics3Dシーン全体を離散化する:
すべての(All)プリミティブを離散化する:
有界区分線形Graphics3Dプリミティブは,厳密に表すことができる:
非有界Graphics3Dプリミティブは,有限範囲でしか表すことができない:
非線形Graphics3Dプリミティブは,近似的にしか表すことができない:
MaxCellMeasureを使って離散化のレベルを制御する:
オプション (23)
MaxCellMeasure (6)
セルの体積のHistogram:
MeshCellHighlight (2)
MeshCellHighlightを使うと,MeshRegionの一部をハイライトするように指定することができる:
MeshCellLabel (3)
MeshCellLabelを使ってMeshRegionの一部にラベルを付けることができる:
MeshCellMarker (1)
MeshCellMarkerを使ってMeshRegionの一部に値を割り当てることができる:
MeshCellLabelを使ってマーカーを示す:
MeshCellShapeFunction (2)
MeshCellStyle (2)
PlotRange (5)
アプリケーション (4)
グラフィックスを幾何学領域に変換し,そのグラフィックスの表面積を計算する:
Textを幾何学領域に変換する:
特性と関係 (9)
BoundaryDiscretizeGraphicsを使ってBoundaryMeshRegion表現を得る:
DiscretizeRegionを使って任意のRegionQオブジェクトを離散化することができる:
DiscretizeGraphicsを使って,GraphicsオブジェクトおよびGraphics3Dオブジェクトを離散化することができる:
両者はどちらも,グラフィックスプリミティブでもある特殊な領域を離散化することができる:
幾何学領域でもあるグラフィックスプリミティブは,離散化なしに使うことができる:
考えられる問題 (4)
Scaled座標のプリミティブは離散化されない:
Offset座標のプリミティブは離散化されない:
ImageScaled座標のプリミティブは離散化されない:
複数の立体プリミティブのあるGraphics3DについてのDiscretizeGraphicsはサポートされていない:

テキスト
Wolfram Research (2014), DiscretizeGraphics, Wolfram言語関数, https://reference.wolfram.com/language/ref/DiscretizeGraphics.html (2015年に更新).
CMS
Wolfram Language. 2014. "DiscretizeGraphics." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/DiscretizeGraphics.html.
APA
Wolfram Language. (2014). DiscretizeGraphics. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscretizeGraphics.html