VectorDisplacementPlot
VectorDisplacementPlot[{vx,vy},{x,xmin,xmax},{y,ymin,ymax}]
生成作为 x 和 y 的函数的矢量场 {vx,vy} 的位移图.
VectorDisplacementPlot[{vx,vy},{x,y}∈reg]
绘制几何区域 reg 上的位移.
VectorDisplacementPlot[{{vx,vy},s},…]
使用标量场 s 来设置位移的样式.
更多信息和选项



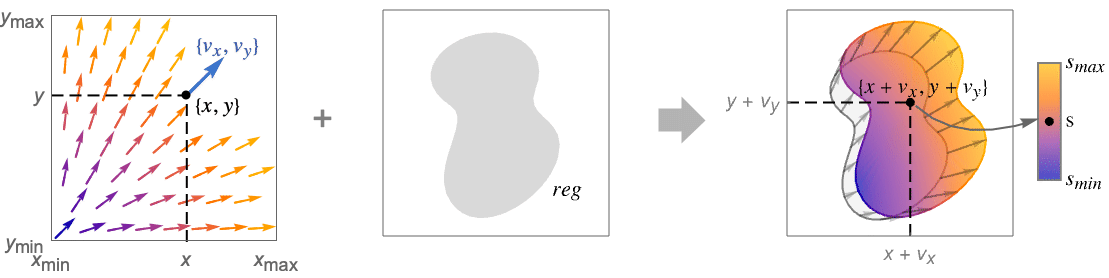
- VectorDisplacementPlot 使用矢量场 {vx,vy} 来置换区域中的点. 默认情况下,位移的大小会自动缩放,以便小位移和大位移都保持可见. 默认情况下,位移区域根据位移的大小着色.
- VectorDisplacementPlot 具有与 Graphics 相同的选项,但有以下添加和更改: [所有选项的列表]
- 默认情况下,位移图显示原始区域和位移区域的表示.
- RegionBoundaryStyle 和 RegionFillingStyle 可用于更改原始区域的样式.
- 用于显示位移箭头的 VectorPoints 的其他设置包括:
-
Automatic 自动选择的点 "Boundary" 沿 reg 边界的点 - 默认情况下,位移箭头将原始区域中的位置与相应的位移位置连接起来.
- VectorSizesFull 显示完整位移而不是缩放表示.
所有选项的列表



范例
打开所有单元关闭所有单元基本范例 (5)
范围 (19)
采样 (12)
演示 (7)
选项 (64)
AspectRatio (2)
BoundaryStyle (3)
ColorFunction (4)
ColorFunctionScaling (2)
Mesh (6)
指定 Mesh 来可视化位移:
PlotRange (3)
PlotStyle (4)
RegionFunction (1)
使用 RegionFunction 指定参考区域:
VectorColorFunction (3)
默认情况下,如果 VectorColorFunction 为 Automatic,则 VectorColorFunction 匹配 ColorFunction:
指定与 ColorFunction 不同的 VectorColorFunction:
不使用 VectorColorFunction:
VectorPoints (9)
VectorSizes (4)
VectorStyle (1)
VectorColorFunction 的优先级高于 VectorStyle:
应用 (24)
基本应用 (16)
使用 VectorSizesFull 显示位移的实际大小:
可视化特征值和特征向量 (1)
固体力学 (5)
考虑一个长度为 ![]() 和高度为
和高度为 ![]() 的线弹性杆在两端承受大小为
的线弹性杆在两端承受大小为 ![]() 时的力矩:
时的力矩:
弹性线(elastica)是一种纤细而有弹性的杆,可以弯曲而不拉伸. 考虑一个最初是直的、垂直的弹性线,它在底端 ![]() 处被夹住,并在顶端加载了一个足够大的重量以使弹性线承重的一端平行于地面. 弧长由下式给出,这是雅各布·伯努利的一个著名发现:
处被夹住,并在顶端加载了一个足够大的重量以使弹性线承重的一端平行于地面. 弧长由下式给出,这是雅各布·伯努利的一个著名发现:
为未变形的弹性线创建一个 ParametricRegion:
考虑一个无限的线弹性薄板,在原点有一个半径为 ![]() 的孔,水平方向上具有均匀的拉伸载荷:
的孔,水平方向上具有均匀的拉伸载荷:
绘制变形的实体区域并通过无量纲环向应力对其进行着色. 注意孔的顶部和底部的应力集中:
定义一个 L 形区域,其底部固定,并在右上角施加均匀拉伸载荷:
考虑固定在 ![]() (红色)处的一个薄的四分之一拱门,在
(红色)处的一个薄的四分之一拱门,在 ![]() (蓝色)处施加可变的垂直牵引力:
(蓝色)处施加可变的垂直牵引力:
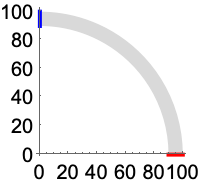
为应变创建一个颜色函数,该函数适用于从零载荷到最大值的所有载荷值:
属性和关系 (9)
使用 ListVectorDisplacementPlot 根据位移场数据可视化变形:
使用 VectorDisplacementPlot3D 可视化与位移矢量场相关的三维区域的变形:
使用 ListVectorDisplacementPlot3D 可视化基于数据的相同的变形:
使用 VectorPlot 直接绘制矢量场:
使用 StreamPlot 用流线而不是矢量绘制:
使用 ListVectorPlot 或 ListStreamPlot 绘制数据:
使用 VectorDensityPlot 添加标量场的密度图:
使用 StreamDensityPlot 绘制流线而不是矢量:
使用 ListVectorDensityPlot 或 ListStreamDensityPlot 绘制数据:
使用 LineIntegralConvolutionPlot 绘制矢量场的线积分卷积:
使用 VectorPlot3D 和 StreamPlot3D 可视化三维矢量场:
使用 ListVectorPlot3D 或 ListStreamPlot3D 绘制数据:
用 SliceVectorPlot3D 在曲面上绘制矢量:
使用 ListSliceVectorPlot3D 绘制数据:
使用 ComplexVectorPlot 或 ComplexStreamPlot 将复变量的复函数可视化为矢量场或流线:
使用 GeoVectorPlot 在地图上绘制矢量:
使用 GeoStreamPlot 绘制流线而不是矢量:
文本
Wolfram Research (2021),VectorDisplacementPlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/VectorDisplacementPlot.html.
CMS
Wolfram 语言. 2021. "VectorDisplacementPlot." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/VectorDisplacementPlot.html.
APA
Wolfram 语言. (2021). VectorDisplacementPlot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/VectorDisplacementPlot.html 年