GeometricScene[{p1,p2,…},{hyp1,hyp2,…}]
represents an abstract 2D geometric scene defined by the hypotheses hypi in terms of the symbolic points pi.
GeometricScene[{{p1,p2,…},{k1,k2,…}},hyps]
represents a scene whose hypotheses depend on the symbolic scalar quantities ki.
GeometricScene[{{p1{x1,y1},…},{k1v1,…}},hyps]
represents a specific instance with explicit values for all points and scalar quantities.
GeometricScene[params,hyps,{con1,con2,…}]
represents a scene together with some conclusions coni about it.
GeometricScene[{{{p1{x1,y1},…},{k1v1,…}},…},hyps]
represents a collection of specific instances of the same scene.
GeometricScene[{scene1,scene2,…}]
combines several scene instances into one scene object.


GeometricScene
GeometricScene[{p1,p2,…},{hyp1,hyp2,…}]
represents an abstract 2D geometric scene defined by the hypotheses hypi in terms of the symbolic points pi.
GeometricScene[{{p1,p2,…},{k1,k2,…}},hyps]
represents a scene whose hypotheses depend on the symbolic scalar quantities ki.
GeometricScene[{{p1{x1,y1},…},{k1v1,…}},hyps]
represents a specific instance with explicit values for all points and scalar quantities.
GeometricScene[params,hyps,{con1,con2,…}]
represents a scene together with some conclusions coni about it.
GeometricScene[{{{p1{x1,y1},…},{k1v1,…}},…},hyps]
represents a collection of specific instances of the same scene.
GeometricScene[{scene1,scene2,…}]
combines several scene instances into one scene object.
Details and Options





- A GeometricScene object with explicit coordinates for all points and explicit values for all scalars is normally displayed as an interactive diagram.
- In GeometricScene[{p1,p2,…},…], the pi can be strings, symbols or other symbolic expressions.
- RandomInstance fills in specific values for the pi and ki in such a way as to satisfy the hypotheses given.
- The hypotheses in a scene can list objects that must appear in the scene and can give relations and other assertions about those objects.
- The following primitives can be used to represent geometric objects:
-
Circle[pt,r] circle Disk[pt,r] filled disk HalfLine[{pt1,pt2}] half-infinite line or ray InfiniteLine[{pt1,pt2}] infinite line Line[{pt1,…}] straight line Parallelogram[pt,{v1,v2}] parallelogram Point[pt] point set Polygon[{pt1,…}] simple polygon Rectangle[pt1,pt2] rectangle RegularPolygon[n] regular polygon Triangle[{pt1,…}] triangle - The points and scalars in a geometric object can be symbolic or can have explicit values.
- The following can be used to represent constructions applied to geometric objects:
-
AngleBisector[{pt1,pt2,pt3}] angle bisector, as an infinite line CircleThrough[{pt1,…}] circle through points CircularArcThrough[{pt1,…}] circular arc through points Circumsphere[{pt1,pt2,pt3}] circumsphere InfiniteLineThrough[{pt1,…}] infinite line through unordered points Insphere[{pt1,pt2,pt3}] insphere Midpoint[{pt1,pt2}] midpoint PerpendicularBisector[{pt1,pt2}] perpendicular bisector, as an infinite line RegionBoundary[reg] boundary RegionCentroid[reg] region centroid, as a point RegionNearest[reg, pt] nearest point in a region TriangleCenter[tri,type] triangle center of specified type TriangleConstruct[tri,type] triangle construct of specified type - The following assertions about geometric objects and their properties can be used:
-
pt∈reg, RegionMember[reg,pt] point is in a region x… equality of values or objects x>…, x<…, … inequalities between values GeometricAssertion[objs,prop] named assertion about geometric objects GeometricStep[{hyp1,hyp2,…}] step consisting of multiple hypotheses - The following measurements on geometric objects can be used:
-
ArcLength[reg] arc length Area[reg] area EuclideanDistance[pt1,pt2] Euclidean distance Perimeter[reg] perimeter PlanarAngle[{pt1,pt2,pt3}] angle PolygonAngle[poly,pt] polygon angle RegionDistance[reg,pt] region distance RegionMeasure[reg] region measure SignedRegionDistance[reg,pt] signed region distance TriangleMeasurement[tri,type] triangle measurement - GeometricScene[…]["prop"] gives property prop of a geometric scene. Possible properties include:
-
"AlgebraicFormulation" algebraic expression giving the constraints on the points and quantities "Conclusions" list of conclusions "Graphics" diagram of the scene, as a Graphics object "GraphicsList" list of Graphics for scenes with multiple steps and/or instances "Hypotheses" list of hypotheses "Instances" list of instances of the scene "Parameters" list of point and scalar value specifications for the scene "Points" list of point specifications for the scene "Properties" list of all supported properties "Quantities" list of scalar value specifications for the scene - With explicit scene instances scenei, GeometricScene[{scene1,scene2,…}] is converted to a GeometricScene object in which multiple lists of points and scalar values are given so long as all the scenei are instances of the same abstract scene.
- When GeometricScene represents multiple instances of an abstract scene, it is normally displayed with a SetterBar to choose which instance to show.
- The display style of geometric objects can be specified using Style. Style specifications do not affect the geometric meaning of a scene.
- GeometricScene accepts options of Graphics, with the following additions: [List of all options]
-
UnconstrainedParameters None list of unconstrained parameters GeometricStylingRules Automatic styling of primitives in the geometric scene PlotTheme $PlotTheme styling of scene as a whole - Functions such as FindGeometricConjectures fill in conclusions in GeometricScene objects.
- Functions such as GeometricSolveValues solve for symbolic geometric quantities in GeometricScene objects. »
-
 Highlight options with settings specific to GeometricScene
Highlight options with settings specific to GeometricScene
-
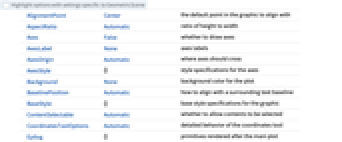
AlignmentPoint Center the default point in the graphic to align with AspectRatio Automatic ratio of height to width Axes False whether to draw axes AxesLabel None axes labels AxesOrigin Automatic where axes should cross AxesStyle {} style specifications for the axes Background None background color for the plot BaselinePosition Automatic how to align with a surrounding text baseline BaseStyle {} base style specifications for the graphic ContentSelectable Automatic whether to allow contents to be selected CoordinatesToolOptions Automatic detailed behavior of the coordinates tool Epilog {} primitives rendered after the main plot FormatType TraditionalForm the default format type for text Frame False whether to put a frame around the plot FrameLabel None frame labels FrameStyle {} style specifications for the frame FrameTicks Automatic frame ticks FrameTicksStyle {} style specifications for frame ticks GeometricStylingRules Automatic styling of primitives in the geometric scene GridLines None grid lines to draw GridLinesStyle {} style specifications for grid lines ImageMargins 0. the margins to leave around the graphic ImagePadding All what extra padding to allow for labels etc. ImageSize Automatic the absolute size at which to render the graphic LabelStyle {} style specifications for labels Method Automatic details of graphics methods to use PlotLabel None an overall label for the plot PlotRange All range of values to include PlotRangeClipping False whether to clip at the plot range PlotRangePadding Automatic how much to pad the range of values PlotRegion Automatic the final display region to be filled PlotTheme $PlotTheme styling of scene as a whole PreserveImageOptions Automatic whether to preserve image options when displaying new versions of the same graphic Prolog {} primitives rendered before the main plot RotateLabel True whether to rotate y labels on the frame Ticks Automatic axes ticks TicksStyle {} style specifications for axes ticks UnconstrainedParameters None list of unconstrained parameters
List of all options
Examples
open all close allBasic Examples (4)
Represent a symbolic geometric scene containing a triangle with points a, b, c and a 30° angle:
RandomInstance fills in explicit coordinates for the points:
Retrieve the rules giving coordinates for the points:
Represent a geometric scene with explicit coordinates for points:
Display an interactive scene that constructs an equilateral triangle in steps:
Consider a scene featuring a right triangle with its leg lengths specified but its hypotenuse ![]() unknown:
unknown:
Use GeometricSolveValues to solve for the hypotenuse ![]() :
:
Scope (4)
Find multiple instances of a scene depicting a triangle, one of whose sides is a diameter of its circumcircle:
Combine the instances into a single GeometricScene object:
Find the coordinates for the points in the scene corresponding to each instance:
Represent a scene depicting line-circle tangency using a GeometricAssertion:
Find conjectures about the scene:
Extract the conclusions from the GeometricScene object:
Represent the construction of the infinite line bisecting the angle formed by points points a, b, c with GeometricStep:
Style can be used to apply styles to objects in a geometric scene:
Options (6)
Applications (7)
Solve for a missing radius, given the radii of four pairwise tangent circles:
Represent a scene with a triangle circumscribed by a circle whose diameter forms an edge:
Represent a scene with two sets of collinear points:
Discover Pappus's hexagon theorem:
Iteratively take circumcenters:
Describe a scene with two squares and a quadrilateral formed by taking midpoints:
Discover the Finsler–Hadwiger theorem:
Bisect a given arc, as specified by Euclid's Book 3, Proposition 30:
Properties & Relations (2)
Geometric scenes with symbolic points do not format:
Geometric scenes where all points have numerical values format graphically:
The conditions for a GeometricScene to hold can be extracted with the subvalue "AlgebraicFormulation":
GeometricTest directly finds these conditions:
These are the same conditions as were returned by the GeometricScene subvalue "AlgebraicFormulation":
See Also
RandomInstance FindGeometricConjectures GeometricSolveValues GeometricAssertion GeometricStep UnconstrainedParameters GeometricStylingRules Graphics
Entity Types: GeometricScene
Function Repository: GeometricSceneConstructor GeometricSolve
Tech Notes
Related Guides
Text
Wolfram Research (2019), GeometricScene, Wolfram Language function, https://reference.wolfram.com/language/ref/GeometricScene.html (updated 2024).
CMS
Wolfram Language. 2019. "GeometricScene." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/GeometricScene.html.
APA
Wolfram Language. (2019). GeometricScene. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GeometricScene.html
BibTeX
@misc{reference.wolfram_2025_geometricscene, author="Wolfram Research", title="{GeometricScene}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/GeometricScene.html}", note=[Accessed: 06-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_geometricscene, organization={Wolfram Research}, title={GeometricScene}, year={2024}, url={https://reference.wolfram.com/language/ref/GeometricScene.html}, note=[Accessed: 06-December-2025]}