関数
| 関数の呼び方 | 一意的な値を持たない関数 |
| 一般解と特殊解 | 数学で用いられる定数 |
| 数値操作関数 | 多項式の直交系 |
| 区分関数 | 特殊関数 |
| 擬似乱数 | 楕円積分と楕円関数 |
| 整数の操作と整数論に関連した関数 | マシューの関数とこれに関連した関数 |
| 組合せ関数 | 特殊関数の取扱い方 |
| 初等超越関数 |
Wolfram言語に組み込まれている関数には,一定の規約に従って名前が付けられている.他のほとんどの組込み関数と同様に,関数にも省略なしの英語単語からなる名前が使われている.例外として,普段よく使う関数には慣用的な省略名が使われている.例えばモジュロ関数がこれに当たり,その関数名はModuloではなくModである.
人名に由来する関数には人名と関数の型を合成した書式 PersonSymbol が使われ名前が付けられている.例えば,ルジャンドル(Legendre)の多項式 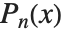 を計算する関数はこの書式に従ってLegendreP[n,x]となる.この呼び方だと関数名が長くなりがちだが,曖昧さや混乱を排除することができる.
を計算する関数はこの書式に従ってLegendreP[n,x]となる.この呼び方だと関数名が長くなりがちだが,曖昧さや混乱を排除することができる.
関数の引数の並び順に関して,上付きと下付きの添字を同時に含む関数では,下付き文字の引数は上付きのものより先に置かれる.つまり,例えば,ルジャンドルの多項式 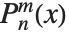 ならLegendreP[n,m,x]と記述される.
ならLegendreP[n,m,x]と記述される.
Wolfram言語がもし自動的に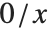 を0で置き換えなかったら,ほとんどの記号計算はあまり先に進まない.この置換操作は実践的な理由で行われるが,パラメータが特殊な値を取る場合には,不正な結果の原因となるので使用には注意しなければならない.
を0で置き換えなかったら,ほとんどの記号計算はあまり先に進まない.この置換操作は実践的な理由で行われるが,パラメータが特殊な値を取る場合には,不正な結果の原因となるので使用には注意しなければならない.
| IntegerPart[x] | x の整数部分 |
| FractionalPart[x] | x の端数部分 |
| Round[x] | x に最も近い整数 〈x〉 |
| Floor[x] | x 以下の最大の整数⌊x⌋ |
| Ceiling[x] | x 以上の最小の整数 ⌈x⌉ |
| Rationalize[x] | x の有理数近似 |
| Rationalize[x,dx] | 許容率 dx 内での有理近似 |
| x | IntegerPart[x] | FractionalPart[x] | Round[x] | Floor[x] | Ceiling[x] |
| 2.4 | 2 | 0.4 | 2 | 2 | 3 |
| 2.5 | 2 | 0.5 | 2 | 2 | 3 |
| 2.6 | 2 | 0.6 | 3 | 2 | 3 |
| -2.4 | -2 | -0.4 | -2 | -3 | -2 |
| -2.5 | -2 | -0.5 | -2 | -3 | -2 |
| -2.6 | -2 | -0.6 | -3 | -3 | -2 |
IntegerPart[x]とFractionalPart[x]は,それぞれ小数点の左側の数値と右側の数値に分けるものととらえることができる.Round[x]は,整数に近い数を強制的に厳密な整数に変換するためによく使われる.Floor[x]とCeiling[x]は,非整数間隔を持つ数の列でいくつ要素があるかを調べるためによく使われる.
| RealSign[x] | x>0であれば1,x<0であれば-1 |
| UnitStep[x] | x≥0のとき1,x<0のとき0 |
| RealAbs[x] | x の絶対値x |
| Clip[x] | x を-1から+1の間で切り取ったものを与える |
| Rescale[x,{xmin,xmax}] | x を0から1の範囲に収まるように再スケールする |
| Max[x1,x2,…] または Max[{x1,x2,…},…] | |
x1, x2, …の中の最大値 | |
| Min[x1,x2,…] または Min[{x1,x2,…},…] | |
x1, x2, …の中の最小値 | |
| x+I y | 複素数 x+iy |
| Re[z] | 実数部分 Re z |
| Im[z] | 虚数部分 Im z |
| Conjugate[z] | 共役複素数 z* または |
| Abs[z] | 絶対値 z |
| Arg[z] | z=zei ϕ の偏角 ϕ |
| Sign[z] | z≠0の複素符号 z/z |
異なる領域に対しては異なる形式の関数があると便利なことが多い.Piecewiseを使うとこうすることができる.
区分関数は異なる領域間を離散的に切り換えるシステムに現れる.これは,スプラインや有限要素を含む多くの計算方法の中心にもなっている.RealAbs,UnitStep,Clip,RealSign,Floor,Max等はその特殊例である.Wolfram言語は区分関数を記号的にも数値的にも扱える.
| RandomInteger[] | 確率を |
| RandomInteger[{imin,imax}] | imin と imax の間の整数の擬似乱数(それぞれを含む) |
| RandomInteger[imax] | 0と imax の間の整数の擬似乱数(それぞれを含む) |
| RandomReal[ ] | 0から1の間の実数値を取る擬似乱数 |
| RandomReal[{xmin, xmax}] | xmin と xmax の間の実数の擬似乱数 |
| RandomReal[xmax] | 0と xmax の間の実数擬似乱数 |
| RandomComplex[] | 単位平方の複素数擬似乱数 |
| RandomComplex[{zmin,zmax}] | zmin と zmax で定義される長方形範囲内の複素数擬似乱数 |
| RandomComplex[zmax] | 0と zmax で定義される長方形範囲内の複素数擬似乱数 |
| RandomReal[range,n]
,
RandomComplex[range,n]
,
RandomInteger[range,n] | |
指定された範囲にある n 個の擬似乱数のリスト | |
| RandomReal[range,{n1,n2,…}]
,
RandomComplex[range,{n1,n2,…}]
,
RandomInteger[range,{n1,n2,…}] | |
擬似乱数の n1×n2×…配列 | |
オプション名
|
デフォルト値
| |
| WorkingPrecision | MachinePrecision | 実数または複素数に使用する精度 |
擬似乱数の一般的な用途として,仮定の数値的な判定への応用がある.例えば,2つのシンボル式が数学的に等しいかどうかを判定するとする.これは,「典型的な」数値をシンボル的パラメータに代入し,数値的な2つの結果を比較することで行うことができる.(ただし,数値精度の問題や,多価複素関数を扱った問題では,このような比較の解釈には注意を要する.)
乱数を代入すると,この等式が常にTrueであるとは限らないことが分かる:
擬似乱数の他の一般的用途として,確率的現象のシミュレーションやサイズの大きい母集団からの標本抽出がある.Wolfram言語が数の範囲に対して生成する乱数は,指定された範囲で必ず一様に分布するようになっている.
関数RandomInteger,RandomReal,RandomComplexは他のほとんどのWolfram言語組込み関数と違った特徴を持っている.つまり,使われるたびに潜在的な出力値は違ってくる.従って,これらを計算でを使うと,答は使うたびに違ってくる.
RandomInteger,RandomReal,RandomComplexで得られる数列は厳密には「真の乱数」ではないが,実用上「十分に乱数的」である.乱数列は,特定の「種(シード)」を開始点として,特定の数学アルゴリズムを適用することで生成される.同じシードが与えられたなら,同じ乱数からなる系列が得られる.
Wolfram言語が起動されたときの時間が(秒以下の精度で記録される)読み込まれ,擬似乱数ジェネレータのシードとして保存される.このため,Wolfram言語を別に起動すれば,擬似乱数列はほとんどいつでも違うものになる.
ここで,毎回必ず同じ乱数系列を使いたいのであれば,同じシードをその都度添加する.このように特別にシードの添加を行うにはSeedRandomを使う.
| SeedRandom[] | その日の時間で,擬似乱数ジェネレータを再びシードする |
| SeedRandom[s] | 整数 s で再びシードする |
RandomInteger,RandomReal,RandomComplexが呼び出されるたびに,それに対応する擬似乱数ジェネレータの内部状態は変わる.従属的な計算でこれらの関数を続けて呼び出すと,主計算に返される数に影響が出るかもしれない.これを防ぐには,BlockRandomの内部で計算を実行することにより関数の使用による影響を局所的なものにするとよい.
| BlockRandom[expr] | 擬似乱数ジェネレータの現在の状態を局所化して,expr を評価する |
BlockRandom内部の計算を局所化することで,リストが生成された後に,擬似乱数ジェネレータの内部状態を復元することができる:
多くの分野で,非一様分布からの乱数が必要とされる.Wolfram言語には多くの分布が組み込まれている.RandomIntegerやRandomRealに対する範囲の代りに適切なパラメータで分布を生成することができる.
| RandomInteger[dist]
,
RandomReal[dist] | |
乱数分布 dist により分布した擬似乱数 | |
| RandomInteger[dist,n]
,
RandomReal[dist,n] | |
乱数分布 dist により分布した n 個の擬似乱数のリスト | |
| RandomInteger[dist,{n1,n2,…}]
,
RandomReal[dist,{n1,n2,…}] | |
乱数分布 dist により分布した擬似乱数の n1×n2×…配列 | |
| RandomChoice[list, n] | list から無作為に n 個の項目を選ぶ |
| RandomChoice[list,{n1,n2,…}] | list から無作為に選ばれた値の n1×n2×…配列 |
| RandomSample[list, n] | list から n を抽出する |
| Mod[k,n] | n を法とする k (k を n で割ったときの剰余) |
| Quotient[m,n] | m と n の商(m/n の整数部) |
| QuotientRemainder[m,n] | 商と剰余のリスト |
| Divisible[m,n] | m が n で割り切れるかどうかのテスト |
| CoprimeQ[n1,n2,…] | ni が対で互いに素であるかどうかのテスト |
| GCD[n1,n2,…] | n1, n2, …の最大公約数 |
| LCM[n1,n2,…] | n1, n2, …の最小公倍数 |
| KroneckerDelta[n1,n2,…] | ni がすべて等しければクロネッカーのデルタ |
| IntegerDigits[n,b] | n を b 進法で表したとき各桁に現れる数 |
| IntegerExponent[n,b] | b を n で割ったときの最大のベキ |
Modには実数を使うこともできる:
Modの結果は,第2引数の符号を引き継ぐ:
| Mod[k,n] | 結果は0から n-1の範囲 |
| Mod[k,n,1] | 結果は1から n の範囲 |
| Mod[k,n,-n/2] | 結果は⌈-n/2⌉から⌊+n/2⌋の範囲 |
| Mod[k,n,d] | 結果は d から d+n-1の範囲 |
特にModを使いオブジェクトの部分の指標を得る場合はオフセットを指定すると便利なことがある.
最大公約数(greatest common divisor)の関数GCD[n1,n2,…]は,すべての ni を割り切ることができる最大整数を与える.2つの整数を比の形で入力したなら,Wolfram言語は,GCDを使い共通因数をキャンセルし,約分し尽くした形の有理数を返す.
| FactorInteger[n] | 整数 n の素因数とその指数のリスト |
| Divisors[n] | n を整除する整数のリスト |
| Prime[k] | k 番目の素数 |
| PrimePi[x] | x 以下の素数がいくつあるか調べる |
| PrimeQ[n] | |
| PrimeNu[n] | n における異なる素数の |
| PrimeOmega[n] | n における重複を数えた素因数 |
| LiouvilleLambda[n] | リウヴィル(Liouville)関数 |
| MangoldtLambda[n] |
マンゴルト(Mangoldt)関数
|
| FactorInteger[n,GaussianIntegers->True] | ガウスの整数 n のガウスの素因数と指数のリスト |
| PrimeQ[n,GaussianIntegers->True] |
数学的に見て,素因数分解は根本的に難解な問題である.このため,キーボードから簡単にタイプできるような整数でも,天文学的に長い時間をかけなければ分解できないことがある.与えられる整数が50桁程度までの大きさならば,Wolfram言語はFactorIntegerを使うことで難なく分解することができる.特別な場合は,それより大きい整数でも分解できる.
デフォルト設定では,FactorInteger は実整数だけを扱う.しかし,GaussianIntegers->Trueのオプション設定が加えられたなら,整数実数部と整数虚数部からなる複素数のガウス整数も扱うことができるようになる.実素数で一意的に分解することが可能なように,ガウス素数で一意的に分解することが可能である.それでもガウス素数を選択するときは潜在的な曖昧さが残る.このため,Wolfram言語では,常に正の実部と負でない虚数部を持つガウス素数が選択される.ただし,最初の素数としては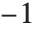 と
と を許容することとする.
を許容することとする.
| PowerMod[a,b,n] | モジュラベキ(ab を n で割った余り) |
| DirichletCharacter[k,j,n] | ディリクレ記号 |
| EulerPhi[n] | オイラー関数 |
| MoebiusMu[n] | メービウスの関数 |
| DivisorSigma[k,n] | 約数関数 |
| DivisorSum[n,form] | n を割り切るすべての i についての form[i]の総和 |
| DivisorSum[n,form,cond] | cond[i]がTrueを与える除数のみの総和 |
| JacobiSymbol[n,m] | ヤコビの記号 |
| ExtendedGCD[n1,n2,…] | n1, n2, …の拡張最大公約数 |
| MultiplicativeOrder[k,n] | k を n で割った余りの乗積順序 |
| MultiplicativeOrder[k,n,{r1,r2,…}] | 剰余 ri の一般化された乗積順序 |
| CarmichaelLambda[n] | カーマイケル関数 |
| PrimitiveRoot[n] | n の原始根 |
PowerModを使えば,正のモジュラベキばかりでなく有限体の逆数も求めることができる.例えば,PowerMod[a,b,n]において b が負の値を取る場合,式 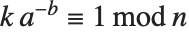 の関係を満たす整数
の関係を満たす整数 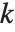 が存在すればそれを与える.(このような整数が存在する場合,それは,必ず n を法(modulo)として一意である.)一方,そのような
が存在すればそれを与える.(このような整数が存在する場合,それは,必ず n を法(modulo)として一意である.)一方,そのような 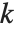 が存在しない場合,PowerModは未評価のまま残される.
が存在しない場合,PowerModは未評価のまま残される.
DirichletCharacterは非常に長い数にも使える:
メービウス(Möbius)の関数 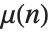 は,
は,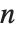 が
が 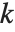 個の異なる素数の積であるとき
個の異なる素数の積であるとき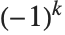 となり,1ではない二乗因数を含む場合に
となり,1ではない二乗因数を含む場合に となるよう定義される.もし,すべての
となるよう定義される.もし,すべての 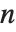 に対して
に対して 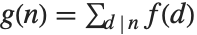 ならば,
ならば,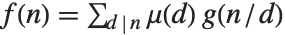 が成り立つ(メービウスの反転公式).ただし,
が成り立つ(メービウスの反転公式).ただし,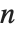 を割り切る正の整数
を割り切る正の整数 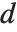 について和を取る.
について和を取る.
関数DivisorSum[n,form]は n を割り切るすべての i についての form[i]の総和を表す.DivisorSum[n,form,cond]は cond[i]がTrueを与える除数だけを含む.
ヤコビ(Jacobi)の記号JacobiSymbol[n,m]は,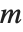 が奇数で,かつ,素数のとき,ルジャンドルの記号
が奇数で,かつ,素数のとき,ルジャンドルの記号 に帰着する.また,ルジャンドルの記号は,
に帰着する.また,ルジャンドルの記号は,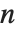 が
が 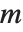 で割り切れるとき0に等しい.そうでない場合,
で割り切れるとき0に等しい.そうでない場合,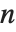 が素数
が素数 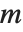 を法とした平方剰余のとき
を法とした平方剰余のとき に等しく,そうでなければ
に等しく,そうでなければ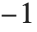 に等しい.ここで,
に等しい.ここで,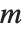 に対して素となる整数
に対して素となる整数 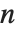 は,
は, の関係を満たす整数
の関係を満たす整数 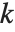 が存在するとき,
が存在するとき,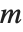 を法とする平方剰余である,という.一般の場合のヤコビの記号は,
を法とする平方剰余である,という.一般の場合のヤコビの記号は,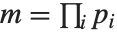 となる各素因数
となる各素因数 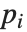 に関するルジャンドルの記号
に関するルジャンドルの記号 の全体の積である.
の全体の積である.
拡張最大公約数ExtendedGCD[n1,n2,…]は,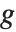 を
を 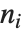 の最大公約数とし,
の最大公約数とし,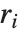 を
を 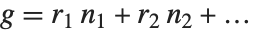 となる整数としたときのリスト
となる整数としたときのリスト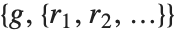 を返す.拡張最大公約数は,線形(不定)方程式の整数解を求める際に重要な役割を果たす.
を返す.拡張最大公約数は,線形(不定)方程式の整数解を求める際に重要な役割を果たす.
一般化された乗積順序関数MultiplicativeOrder[k,n,{r1,r2,…}]は任意の 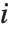 に対して
に対して 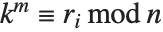 が成り立つような最小の整数
が成り立つような最小の整数 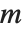 を与える.MultiplicativeOrder[k,n,{-1,1}]は
を与える.MultiplicativeOrder[k,n,{-1,1}]は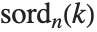 と表記され
と表記され 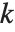 を
を 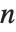 で法とする部分順序関数として知られている.MultiplicativeOrder[k,n,{a}]は
で法とする部分順序関数として知られている.MultiplicativeOrder[k,n,{a}]は 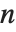 を法とする基底
を法とする基底 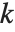 に関する
に関する 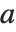 の離散対数としても知られている.
の離散対数としても知られている.
| ContinuedFraction[x,n] | x の連分数表現の最初の n 項を生成する |
| FromContinuedFraction[list] | 連分数表現から数値を再構築する |
| Rationalize[x,dx] | 許容率 dx で x の有理近似を求める |
| ContinuedFraction[x] | 有理数または二次無理数の完全な連分数表現 |
| QuadraticIrrationalQ[x] | x が二次無理数であるかどうかをテストする |
| RealDigits[x] | 有理数の完全な数列 |
| RealDigits[x,b] | b を基底とする完全な数列 |
FromDigitsはもとの数値を再構築する:
連分数の近似分数は無理数を有理数で近似するときによく使われる.この近似は上と下から交互に起り,項の数で指数関数的に収束する.さらに,単純な連分数の近似分数 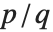 は分母が
は分母が 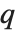 以下の他のどのような有理近似よりもよいものとなる.
以下の他のどのような有理近似よりもよいものとなる.
| Convergents[x] | x の有理近似のリストを与える |
| Convergents[x,n] | 最初の n 個の近似だけを与える |
| LatticeReduce[{v1v2,…}] | 整数ベクトル vi の集合に対する格子基底縮小 |
| HermiteDecomposition[{v1,v2,…}] | 整数ベクトル vi の集合に対する階段型 |
格子縮小関数LatticeReduce[{v1,v2,…}]は,現代のアルゴリズムの数種類で使われる.この基本的な考え方は,整数のベクトル 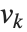 を数学的な「格子」として考えることである.格子の中の点を表すベクトルはすべて形式
を数学的な「格子」として考えることである.格子の中の点を表すベクトルはすべて形式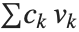 (
(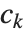 は整数)の線形結合として書くことができる.特定の格子では,「基底ベクトル」
は整数)の線形結合として書くことができる.特定の格子では,「基底ベクトル」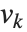 に対して多くの選択肢がある.LatticeReduceが行うのは,ある特定の性質を持つ,この格子の基底ベクトル
に対して多くの選択肢がある.LatticeReduceが行うのは,ある特定の性質を持つ,この格子の基底ベクトル 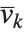 の縮小集合を見付けることである.
の縮小集合を見付けることである.
最後の例では,LatticeReduceはほぼ平行なベクトルをより垂直なベクトルで置き換えている.この過程で,非常に短い基底ベクトルが見付かる.
行列 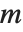 では,HermiteDecompositionは
では,HermiteDecompositionは 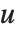 がユニモジュラ,
がユニモジュラ,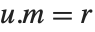 ,
,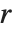 が行縮小形式となるような行列
が行縮小形式となるような行列 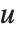 と
と 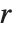 を与える.RowReduceとは対照的に,整数環には分数はないので,軸は1より大きいことがある.軸より上の要素は,軸の行の適切な倍数を引くことにより最小化される.
を与える.RowReduceとは対照的に,整数環には分数はないので,軸は1より大きいことがある.軸より上の要素は,軸の行の適切な倍数を引くことにより最小化される.
| DigitCount[n,b,d] | n を基底 b で表現したときに現れる数 d の個数 |
| BitAnd[n1,n2,…] | 整数 ni のビットごとのAND |
| BitOr[n1,n2,…] | 整数 ni のビットごとのOR |
| BitXor[n1,n2,…] | 整数 ni のビットごとのXOR |
| BitNot[n] | 整数 n のビットごとのNOT |
| BitLength[n] | 整数 n のバイナリビットの数 |
| BitSet[n,k] | 整数 n でビット k を1に設定する |
| BitGet[n,k] | 整数 n からビット k を得る |
| BitClear[n,k] | 整数 n のビット k を0に設定する |
| BitShiftLeft[n,k] | 整数 n を k ビットだけ左にシフトし,ゼロで充填する |
| BitShiftRight[n,k] | 右にシフトし,最後の k ビットを削除する |
ビットごとの演算はバイナリビットで表現された整数に施される.BitAnd[n1,n2,…]はバイナリビット表現で ni のすべてに1がある場所に,バイナリ表現で1がある整数を与える.BitOr[n1,n2,…]はバイナリビット表現で任意の ni に1がある場所に1がある整数を与える.BitXor[n1,n2]は n1または n2のどちらかだけに1がある場所にバイナリビット表現で1がある整数を与える.BitXor[n1,n2,…]は奇数個の ni に1がある場所に1がある整数を与える.
ビットごとの演算は様々な組合せ論アルゴリズムで使用される.また低レベルのコンピュータ言語でもビットフィールドの操作によく使用される.しかしそれらの言語では整数は通常は8の倍数であるような限られた桁数しか許されない.Wolfram言語でのビットごとの演算では無限の桁数の整数を扱うことができる.負の整数の場合は,左に1の数列が無限にあるような2の補数で表現される.これによりBitNot[n]は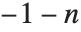 と同等となる.
と同等となる.
| SquareFreeQ[n] |
SquareFreeQ[n]は n が平方の素因数を持つかどうかを確認する.これはを計算し,結果がゼロであるかどうかを見て行われる.ゼロの場合は n は無平方ではなく,ゼロでない場合は無平方である.MoebiusMu[n]の計算を行うと,n の最小の素因数 q が求められる.n が 以下の小さな素因数を持つ場合は,MoebiusMu[n]の計算は非常に速い.持たない場合は,q を求めるのにFactorIntegerが使われる.
以下の小さな素因数を持つ場合は,MoebiusMu[n]の計算は非常に速い.持たない場合は,q を求めるのにFactorIntegerが使われる.
SquareFreeQは大きな整数にも対応できる:
| NextPrime[n] | n より大きい最小の素数を返す |
| RandomPrime[{min,max}] | min より大きく max より小さいランダムな素数を返す |
| RandomPrime[max] | max より小さいか等しいランダムな素数を返す |
| RandomPrime[{min,max},n] | min より大きく max より小さい n 個のランダムな素数を返す |
| RandomPrime[max,n] | maxより小さいか等しいランダムな素数を n 個返す |
RandomPrime[{min,max}]とRandomPrime[max]については,ランダムな素数 p は,max が小さな場合は素数参照表からランダムに選択し,max が大きな場合にはその範囲内の整数のランダム検索で求める.指定の範囲に素数が存在しない場合は,入力は評価されずに返され,エラーメッセージが表示される.
| PrimePowerQ[n] | n が有理数の素数の正の整数ベキであるかどうかを判別する |
PrimePowerQのアルゴリズムは,まず n の最小の素因数 p を計算し,次に1が得られるまで(この場合,n は素数のベキ乗),または不可能になるまで(この場合,n は素数のベキ乗ではない)p による除算を試みる.
GaussianIntegers上では,これは素数ベキである:
| ChineseRemainder[list1,list2] | Mod[r,list2]==list1である非負の最小の整数 r を返す |
中国余剰定理(Chinese Remainder Theorem)によると,連立合同式のある特定のクラスには常に解が存在する.ChineseRemainder[list1,list2]を使うと,Mod[r,list2]が list1である非負の最小の整数 r が求められる.解は list2の要素の最小公倍数の唯一のモジュロである.
| PrimitiveRoot[n] | n の原始根を1つ返す.n は素数のベキか素数のベキの2倍である |
PrimitiveRoot[n]は, の乗算で,n と互いに素である数の群の生成元を返す.生成元は n が2,4,奇数の素数のベキ乗,または奇数の素数のベキ乗の2倍である場合にのみ存在する.n が素数または素数のベキ乗の場合は,正の最小の原始根が返される.
の乗算で,n と互いに素である数の群の生成元を返す.生成元は n が2,4,奇数の素数のベキ乗,または奇数の素数のベキ乗の2倍である場合にのみ存在する.n が素数または素数のベキ乗の場合は,正の最小の原始根が返される.
| SquaresR[d,n] | 整数 n を d 個の2乗の数の和として表したときの表記の数を返す |
| PowersRepresentations[n,k,p] | 整数 n を非負の p 番目の整数ベキ k 個の和として表す方法を返す |
| n! | 階乗 |
| n!! | 二重階乗 |
| Binomial[n,m] | 二項係数 |
| Multinomial[n1,n2,…] | 多項係数 |
| CatalanNumber[n] | カタラン(Catalan)数 |
| Hyperfactorial[n] | 超階乗 |
| BarnesG[n] | バルネス(Barnes)のG関数 |
| Subfactorial[n] | |
| Fibonacci[n] | フィボナッチ(Fibonacci)数 |
| Fibonacci[n,x] | フィボナッチ多項式 |
| LucasL[n] | リュカ(Lucas)数 |
| LucasL[n,x] | リュカ多項式 |
| HarmonicNumber[n] | 調和数 |
| HarmonicNumber[n,r] | |
| BernoulliB[n] | ベルヌーイ(Bernoulli)数 |
| BernoulliB[n,x] | ベルヌーイ多項式 |
| NorlundB[n,a] | ネールルンド(Nörlund)多項式 |
| NorlundB[n,a,x] | 一般化されたベルヌーイ多項式 |
| EulerE[n] | オイラー(Euler)数 |
| EulerE[n,x] | オイラーの多項式 |
| StirlingS1[n,m] | 第一種のスターリング(Stirling)数 |
| StirlingS2[n,m] | 第二種のスターリング数 |
| BellB[n] | ベル(Bell)数 |
| BellB[n,x] | ベル多項式 |
| PartitionsP[n] | 整数 |
| IntegerPartitions[n] | 整数の分け方 |
| PartitionsQ[n] | 整数 |
| Signature[{i1,i2,…}] | 順列の符号 |
二項係数の関数Binomial[n,m]は,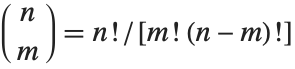 と書ける.この関数は,並び順を考慮しないとき,
と書ける.この関数は,並び順を考慮しないとき,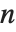 個のものの中からの
個のものの中からの 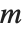 個のものの取出し方の数を与える.また,各種の木の枚挙問題に現れるカタラン数は,二項係数により,
個のものの取出し方の数を与える.また,各種の木の枚挙問題に現れるカタラン数は,二項係数により,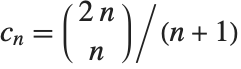 の関係式で与えられる.
の関係式で与えられる.
フィボナッチの数Fibonacci[n]は,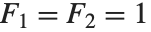 のときに漸化式
のときに漸化式 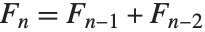 を満たす.この数は離散数学で広く使われる.
を満たす.この数は離散数学で広く使われる.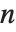 を増加させると,
を増加させると,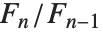 は黄金比に近付く.リュカ数LucasL[n]は,初期値が
は黄金比に近付く.リュカ数LucasL[n]は,初期値が  と
と 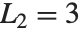 の,フィボナッチ数と同じ循環関係を満足する.
の,フィボナッチ数と同じ循環関係を満足する.
調和数HarmonicNumber[n]は  で与えられる.
で与えられる.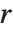 次の調和数HarmonicNumber[n,r]は
次の調和数HarmonicNumber[n,r]は  で与えられる.調和数は多くの組合せ論の推定問題で現れ,しばしば離散化された対数に相当する役割を演じる.
で与えられる.調和数は多くの組合せ論の推定問題で現れ,しばしば離散化された対数に相当する役割を演じる.
ベルヌーイの多項式BernoulliB[n,x]は,母関数の関係式 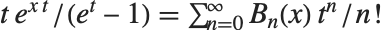 を満たす.また,ベルヌーイ数BernoulliB[n]は,
を満たす.また,ベルヌーイ数BernoulliB[n]は,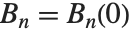 で与えられる.
で与えられる.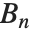 は,近似積分で使われるオイラー・マクローリン(Euler–Maclaurin)総和の式における項の係数に当たる.ベルヌーイ数はジェノッチ数と
は,近似積分で使われるオイラー・マクローリン(Euler–Maclaurin)総和の式における項の係数に当たる.ベルヌーイ数はジェノッチ数と 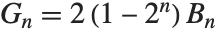 の関係にある.
の関係にある.
ネールルンド多項式NorlundB[n,a]は母関数の関係式 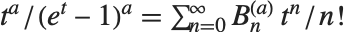 を満足する.ネールルンドは,
を満足する.ネールルンドは, のときベルヌーイ数を返す.
のときベルヌーイ数を返す.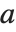 が他の正の整数値である場合,ネールルンド多項式は高次のベルヌーイ数を返す.一般化されたベルヌーイ多項式NorlundB[n,a,x] は,母関数の関係式
が他の正の整数値である場合,ネールルンド多項式は高次のベルヌーイ数を返す.一般化されたベルヌーイ多項式NorlundB[n,a,x] は,母関数の関係式 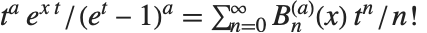 を満足する.
を満足する.
BernoulliB[n]は,ベルヌーイ数を厳密な有理数として返す:
スターリング数は組合せ理論の枚挙問題によく現れる.第一種のスターリング数StirlingS1[n,m]に対して,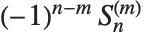 は,ちょうど
は,ちょうど 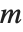 回循環する
回循環する 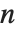 個の要素の順列の個数を返す.スターリング数は,母関数の関係式
個の要素の順列の個数を返す.スターリング数は,母関数の関係式  を満たす.注意点として,
を満たす.注意点として,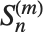 の定義によっては,
の定義によっては,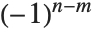 の係数が付くためWolfram言語の定義と異なる場合がある.
の係数が付くためWolfram言語の定義と異なる場合がある.
第二種のスターリング数StirlingS2[n,m]は 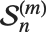 と記述されることもあるが,
と記述されることもあるが,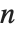 個の要素を空でない
個の要素を空でない 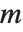 組の部分集合に分ける上で何通りの分け方があるかを返す.第二種のスターリング数は,
組の部分集合に分ける上で何通りの分け方があるかを返す.第二種のスターリング数は,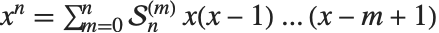 の関係式を満たす.
の関係式を満たす.
分割関数PartitionsP[n]は,整数 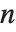 を正整数の和として順不同で組み合すとき,組合せ方が何通りあるかを返す.PartitionsQ[n]は,和を構成する整数成分が相異するとき,整数
を正整数の和として順不同で組み合すとき,組合せ方が何通りあるかを返す.PartitionsQ[n]は,和を構成する整数成分が相異するとき,整数 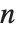 の組合せ方が何通りあるかを返す.
の組合せ方が何通りあるかを返す.
分割数はPartitionsP[4]で与えられる:
ここで説明してきた関数のほとんどは,各種の組合せの数を数えるのに使われる.これらとは違って,IntegerPartitionsやPermutationsのような関数は,要素の組合せそのもののリストを生成するために使われる.
符号関数Signature[{i1,i2,…}]は順列の符号を返す.偶順列なら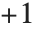 を返し,奇順列なら
を返し,奇順列なら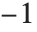 を返す.偶順列(もしくは,奇順列)とは順列が偶数回(奇数回)の互換(2つの要素の入れ替え)で得られることを指す.符号関数は,交代テンソルであるレヴィ・チヴィタ(Levi‐Civita)の記号,または,イプシロン記号としてとらえることができる.
を返す.偶順列(もしくは,奇順列)とは順列が偶数回(奇数回)の互換(2つの要素の入れ替え)で得られることを指す.符号関数は,交代テンソルであるレヴィ・チヴィタ(Levi‐Civita)の記号,または,イプシロン記号としてとらえることができる.
| ClebschGordan[{j1,m1},{j2,m2},{j,m}] |
クレプシュ・ゴルダン(Clebsch
–
Gordan)の係数
|
| ThreeJSymbol[{j1,m1},{j2,m2},{j3,m3}] | ウィグナー(Wigner)の3–j 記号 |
| SixJSymbol[{j1,j2,j3},{j4,j5,j6}] | ラカー(Racah)の6–j 記号 |
クレプシュ・ゴルダンの係数と 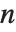 –j記号は,量子力学における角運動量の解析や,その他の回転群の応用の問題で使われる.クレプシュ・ゴルダンの係数ClebschGordan[{j1,m1},{j2,m2},{j,m}]は,量子化された角運動量の状態
–j記号は,量子力学における角運動量の解析や,その他の回転群の応用の問題で使われる.クレプシュ・ゴルダンの係数ClebschGordan[{j1,m1},{j2,m2},{j,m}]は,量子化された角運動量の状態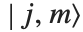 を展開したとき得られる項の係数を状態
を展開したとき得られる項の係数を状態 の積で与える.
の積で与える.
3–j記号あるいはウィグナー係数のThreeJSymbol[{j1,m1},{j2,m2},{j3,m3}]は,クレプシュ・ゴルダンの係数より高い対称性を持つ.Wolfram言語における定義では,クレプシュ・ゴルダンの係数は,3–j記号に基づいた 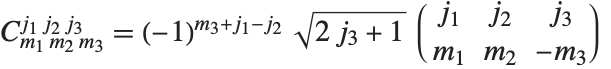 の関係式で与えられる.
の関係式で与えられる.
| Exp[z] | 指数関数 |
| Log[z] | 自然対数関数 |
| Log[b,z] | |
| Log2[z]
,
Log10[z] | 底を2および10とする対数関数 |
| Sin[z]
,
Cos[z]
,
Tan[z]
,
Csc[z]
,
Sec[z]
,
Cot[z] | |
三角関数 (引数はラジアン) | |
| ArcSin[z]
,
ArcCos[z]
,
ArcTan[z]
,
ArcCsc[z]
,
ArcSec[z]
,
ArcCot[z] | |
逆三角関数 (結果はラジアン) | |
| ArcTan[x,y] | |
| Sinh[z]
,
Cosh[z]
,
Tanh[z]
,
Csch[z]
,
Sech[z]
,
Coth[z] | |
双曲線関数 | |
| ArcSinh[z]
,
ArcCosh[z]
,
ArcTanh[z]
,
ArcCsch[z]
,
ArcSech[z]
,
ArcCoth[z] | |
逆双曲線関数 | |
| Sinc[z] | シンク関数 |
| Haversine[z] | 半正矢関数 |
| InverseHaversine[z] | 半正矢関数の逆関数 |
| Gudermannian[z] | グーデルマン関数 |
| InverseGudermannian[z] | グーデルマン関数の逆関数 |
特別に定数Degreeを掛けておけば,度数でも入力することができる:
半正矢関数Haversine[z]は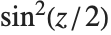 で定義される.半正矢関数の逆関数InverseHaversine[z]は
で定義される.半正矢関数の逆関数InverseHaversine[z]は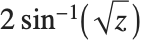 で定義される.グーデルマン関数Gudermannian[z]は
で定義される.グーデルマン関数Gudermannian[z]は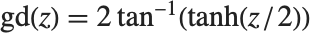 として定義され,その逆関数InverseGudermannian[z]は
として定義され,その逆関数InverseGudermannian[z]は で定義さえる.グーデルマン関数は
で定義さえる.グーデルマン関数は の関係を満足する.シンク関数Sinc[z]は平方信号のフーリエ変換である.
の関係を満足する.シンク関数Sinc[z]は平方信号のフーリエ変換である.
2つの解から単一の解を選ばなければならないということは,Sqrt[x]の操作は,x^2の真の逆関数ではないということになる.つまり,与えられた数の二乗を取り,二乗した値から平方根を求めても必ずしももとの数は得られない.
実際,すべての複素数 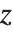 に対して連続となるように
に対して連続となるように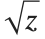 の値を選択することは不可能である.複素平面上に「分岐」と呼ばれる半直線を設定し,その半直線を越えて動くとき
の値を選択することは不可能である.複素平面上に「分岐」と呼ばれる半直線を設定し,その半直線を越えて動くとき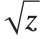 は不連続となる.Wolfram言語では,
は不連続となる.Wolfram言語では,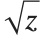 に対する分岐を負の実軸に沿うものとする標準的な規約が使われている.
に対する分岐を負の実軸に沿うものとする標準的な規約が使われている.
平方根のような,基本的に方程式の解を見出す関数がいくつもある.対数関数や逆三角関数もこの種の関数に当たる.これらを使うほとんどの方程式問題では,方程式には複数の解が存在する.それでも,一意的な「主」値を選択する必要がある.このとき,全複素平面において連続となる主値を選択することはできない.このため,不連続な線,つまり,分岐が存在する必要がある.これらの分岐をどの位置に取るかは本来任意である.Wolfram言語では,数学で最も標準的とされる分岐位置が採用されている.
| Sqrt[z] および z^s | |
| Exp[z] | なし |
| Log[z] | |
三角関数 | なし |
| ArcSin[z] および ArcCos[z] | |
| ArcTan[z] | |
| ArcCsc[z] および ArcSec[z] | |
| ArcCot[z] | |
双曲線関数 | なし |
| ArcSinh[z] | |
| ArcCosh[z] | |
| ArcTanh[z] | |
| ArcCsch[z] | |
| ArcSech[z] | |
| ArcCoth[z] |
分岐の両側において,ArcSin[z]の値は大きく異なる:
| I | |
| Infinity | |
| Pi | |
| Degree | |
| GoldenRatio | |
| E | |
| EulerGamma | オイラーの定数 |
| Catalan | カタランの定数 |
| Khinchin | ヒンチンの定数 |
| Glaisher | グレシャーの定数 |
オイラーの定数EulerGammaは  の極限として与えられる.さまざまな積分や漸近式に使われる.オイラーの定数はオイラー・マスケロニ(Euler‐Mascheroni)の定数とも呼ばれ,
の極限として与えられる.さまざまな積分や漸近式に使われる.オイラーの定数はオイラー・マスケロニ(Euler‐Mascheroni)の定数とも呼ばれ,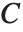 で記されることもある.
で記されることもある.
グレシャー(Glaisher)の定数Glaisher 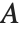 (グレシャー・キンキリン(Glaisher‐Kinkelin)の定数とも呼ばれる)は
(グレシャー・キンキリン(Glaisher‐Kinkelin)の定数とも呼ばれる)は 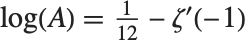 を満足する.ここで
を満足する.ここで  はリーマンのゼータ関数である.特にガンマ関数およびゼータ関数を含む,各種総和および積分で使用される.
はリーマンのゼータ関数である.特にガンマ関数およびゼータ関数を含む,各種総和および積分で使用される.
| LegendreP[n,x] | ルジャンドルの多項式 |
| LegendreP[n,m,x] | ルジャンドルの陪多項式 |
| SphericalHarmonicY[l,m,θ,ϕ] | 球面調和関数 |
| GegenbauerC[n,m,x] | ゲーゲンバウアの多項式 |
| ChebyshevT[n,x]
,
ChebyshevU[n,x] | |
第一種チェビシェフの多項式 | |
| HermiteH[n,x] | エルミートの多項式 |
| LaguerreL[n,x] | ラゲールの多項式 |
| LaguerreL[n,a,x] | ラゲールの一般化多項式 |
| ZernikeR[n,m,x] | ゼルニケのラジアル多項式 |
| JacobiP[n,a,b,x] | ヤコビの多項式 |
ルジャンドルの陪多項式LegendreP[n,m,x]は,ルジャンドルの多項式の導関数を用いて 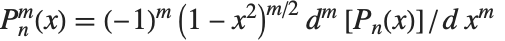 で与えられる.奇数の整数
で与えられる.奇数の整数  とき,
とき,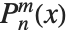 は
は のベキを含むため,厳密には多項式にならないことに注意のこと.また,
のベキを含むため,厳密には多項式にならないことに注意のこと.また, のとき,
のとき,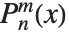 は
は 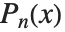 に帰着する.
に帰着する.
球面調和関数SphericalHarmonicY[l,m,θ,ϕ]は,ルジャンドルの陪多項式に関連して定義される.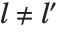 または
または 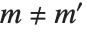 のとき,同関数は直交関係
のとき,同関数は直交関係 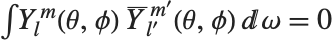 を満たす.ここで
を満たす.ここで 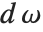 は単位球面について積分することを示す.
は単位球面について積分することを示す.
「特殊関数」にあるように,ルジャンドルの多項式は非整数の次数を持つルジャンドル関数に一般化される:
ゲーゲンバウア(Gegenbauer)の多項式GegenbauerC[n,m,x]は,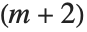 次元の球対称の系に対して一般化されたルジャンドルの多項式と見ることができる.また,このために超球関数とも呼ばれる.
次元の球対称の系に対して一般化されたルジャンドルの多項式と見ることができる.また,このために超球関数とも呼ばれる.
チェビシェフ(Chebyshev)の多項式は関数の近似値を求めるのによく使われる.第一種チェビシェフの多項式ChebyshevT[n,x]は  で定義され,
で定義され,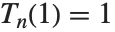 になるように標準化されている.この多項式は
になるように標準化されている.この多項式は 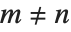 のとき,直交関係
のとき,直交関係 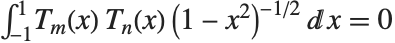 を満たす.さらに,
を満たす.さらに,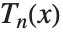 は
は 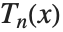 の根に相当する
の根に相当する 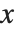 の離散点で和を取っても直交関係を満たす.
の離散点で和を取っても直交関係を満たす.
エルミート(Hermite)の多項式HermiteH[n,x]は,量子力学における調和振動子の波動関数に使われる.これは,微分方程式 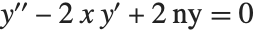 を満たし,さらに
を満たし,さらに 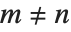 のとき,直交関係
のとき,直交関係 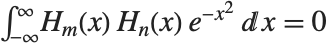 を満たす.エルミートの多項式はこの他に
を満たす.エルミートの多項式はこの他に 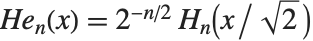 という別の形も使われることがある.(
という別の形も使われることがある.(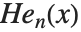 の,全く異なる標準化が用いられることもある.)
の,全く異なる標準化が用いられることもある.)
ラゲール(Laguerre)の一般多項式LaguerreL[n,a,x]は,量子力学における水素原子の波動関数に関係している.同多項式は,微分方程式 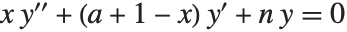 を満たし,さらに
を満たし,さらに 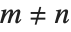 のとき直交関係
のとき直交関係 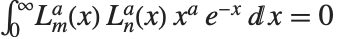 も満たす.ラゲールの多項式LaguerreL[n,x]は,一般式の特殊な場合
も満たす.ラゲールの多項式LaguerreL[n,x]は,一般式の特殊な場合  に対応している.
に対応している.
ヤコビの多項式JacobiP[n,a,b,x]は,量子力学等の回転群の問題でよく使われる.同多項式は,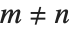 のとき直交関係
のとき直交関係 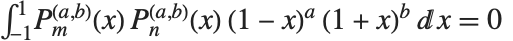 を満たす.ルジャンドル,ゲーゲンバウア,チェビシェフの多項式はすべてヤコビの多項式の特殊形ともみなせる.ヤコビの多項式が
を満たす.ルジャンドル,ゲーゲンバウア,チェビシェフの多項式はすべてヤコビの多項式の特殊形ともみなせる.ヤコビの多項式が 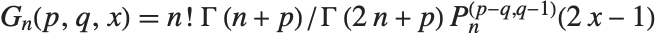 の関係式で定義されるときもある.
の関係式で定義されるときもある.
FindRootを使い,特殊関数であっても,その根を探すことができる:
Wolframシステムにおいて特殊関数は,通常任意の複素数の引数に対して評価することができる.しかし,多くの場合,このチュートリアルで示す定義関係式は,引数が特定の値を取るときに限り有効となる.そのような場合,完全な関数はこれらの関係式の適正な拡張,つまり「解析接続」に対応する.例えば,関数の積分表記は,該当する積分が存在するときに限って有効であるが,関数自体は解析接続により別の点においても通常定義することができる.
関数の定義域をどう拡張できるか,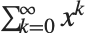 の簡単な和を例に考えてみる.和は
の簡単な和を例に考えてみる.和は のときだけに収束する.それでも,任意の
のときだけに収束する.それでも,任意の 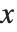 に対して,この和を解析接続して得られる関数が
に対して,この和を解析接続して得られる関数が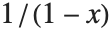 に等しい,ということは簡単に解析的に証明できる.この形を使うことで,少なくとも
に等しい,ということは簡単に解析的に証明できる.この形を使うことで,少なくとも 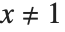 でさえあれば,任意の
でさえあれば,任意の 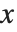 に対して,和の関数の値を簡単に求めることができる.
に対して,和の関数の値を簡単に求めることができる.
ガンマ関数とこれに関連した関数
| Beta[a,b] | オイラーのベータ関数 |
| Beta[z,a,b] | 不完全ベータ関数 |
| BetaRegularized[z,a,b] | 正則化された不完全ベータ関数 |
| Gamma[z] | オイラーのガンマ関数 |
| Gamma[a,z] | 不完全ガンマ関数 |
| Gamma[a,z0,z1] | 一般化された不完全ガンマ関数 |
| GammaRegularized[a,z] | 正則化された不完全ガンマ関数 |
| InverseBetaRegularized[s,a,b] | 正則化された逆ベータ関数 |
| InverseGammaRegularized[a,s] | 正則化された逆ガンマ関数 |
| Pochhammer[a,n] | ポッホハンマーの記号 |
| PolyGamma[z] | ディガンマ関数 |
| PolyGamma[n,z] | ディガンマ関数の |
| LogGamma[z] | オイラーの対数ガンマ関数 |
| LogBarnesG[z] | バルネスのG関数の対数 |
| BarnesG[z] | バルネスのG関数 |
| Hyperfactorial[n] | 超階乗関数 |
特に整数論の計算では,ガンマ関数に対する対数が現れることがある.引数が正の実数のとき,これは,単に,Log[Gamma[z]]とすることで評価することができる.しかし,引数が複素数のときは,不規則な不連続点が発生してしまう.このため,Wolframシステムには,LogGamma[z]と呼ばれる関数が特別に定義してある.同関数は,負の実軸に沿って分岐を持たせたガンマ関数の対数を与える.
ポッホハンマー(Pochhammer)の記号あるいは昇階乗Pochhammer[a,n]は,関係式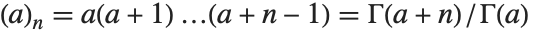 で定義される.この関数は超幾何関数の級数展開でよく使われる.注意点として,定義式にあるガンマ関数が無限大になるときでも,ポッホハンマーの記号の値は確定する.
で定義される.この関数は超幾何関数の級数展開でよく使われる.注意点として,定義式にあるガンマ関数が無限大になるときでも,ポッホハンマーの記号の値は確定する.
不完全ベータ関数Beta[z,a,b]は,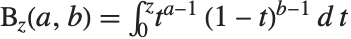 で与えられる.不完全ベータ関数では,関数の第1引数であるパラメータ
で与えられる.不完全ベータ関数では,関数の第1引数であるパラメータ 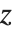 が積分の上限を特定していることに注意する.これに対して,不完全ガンマ関数では,関数の第2引数の
が積分の上限を特定していることに注意する.これに対して,不完全ガンマ関数では,関数の第2引数の 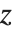 が積分の下限を特定する.
が積分の下限を特定する.
不完全ベータ関数および不完全ガンマ関数はそのまま計算せずに,まず,正則化された形を求めた方が計算しやすくなることがある.ここで,正規形とは,完全ベータ関数(もしくは,完全ガンマ関数)で不完全形を割った形を意味する.不完全ベータ関数を正則化した関数としてBetaRegularized[z,a,b]が用意されている.この関数は,引数のほとんどの値域で  の関係で定義され,特異点も扱うことができる.また,不完全ガンマ関数を正則化した関数GammaRegularized[a,z]は
の関係で定義され,特異点も扱うことができる.また,不完全ガンマ関数を正則化した関数GammaRegularized[a,z]は  の関係で定義され,特異点も扱うことができる.
の関係で定義され,特異点も扱うことができる.
不完全ベータ関数と不完全ガンマ関数,および,それらの逆関数は,統計でよく使われる.逆ベータ関数InverseBetaRegularized[s,a,b]は, における
における 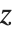 の解である.同様に,逆ガンマ関数InverseGammaRegularized[a,s]は,
の解である.同様に,逆ガンマ関数InverseGammaRegularized[a,s]は,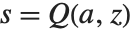 における
における 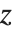 の解である.
の解である.
ガンマ関数の導関数が有理級数の和を求めるときによく使われる.ディガンマ関数PolyGamma[z]は 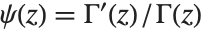 で与えられ,ガンマ関数の対数微分である.引数が整数のとき,ディガンマ関数は関係式
で与えられ,ガンマ関数の対数微分である.引数が整数のとき,ディガンマ関数は関係式 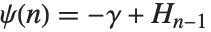 を満たす.ここで,
を満たす.ここで,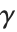 はオイラー定数(WolframシステムではEulerGamma)を示し,
はオイラー定数(WolframシステムではEulerGamma)を示し,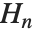 は調和数を示す.
は調和数を示す.
ポリガンマ関数PolyGamma[n,z]は,微分式 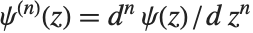 で与えられる.ディガンマ関数は,
で与えられる.ディガンマ関数は,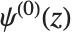 に対応している.また,
に対応している.また,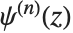 がガンマ関数の
がガンマ関数の  階の対数微分であり,
階の対数微分であり,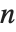 階ではないことに注意する.また,ポリガンマ関数は関係式
階ではないことに注意する.また,ポリガンマ関数は関係式 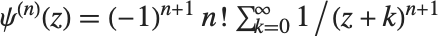 を満たす.PolyGamma[ν,z]は,任意の複素数
を満たす.PolyGamma[ν,z]は,任意の複素数 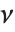 について分数計算の解析接続によって与えられる.
について分数計算の解析接続によって与えられる.
BarnesG[z]はGamma関数の一般化であり,その機能の同一性BarnesG[z+1]=Gamma[z] BarnesG[z]により定義される.一方,BarnesGの対数の第3導関数は正の z に対して正である.BarnesGは複素平面上の整関数である.
ゼータ関数とこれに関連した関数
| DirichletL[k,j,s] | ディリクレのL関数 |
| LerchPhi[z,s,a] | レルヒの超越関数 |
| PolyLog[n,z] | 多重対数関数 |
| PolyLog[n,p,z] | ニールセンの一般化された多重対数関数 |
| RamanujanTau[n] | ラマヌジャンの |
| RamanujanTauL[n] | ラマヌジャンの |
| RamanujanTauTheta[n] | ラマヌジャンの |
| RamanujanTauZ[n] | ラマヌジャン |
| RiemannSiegelTheta[t] | マン・ジーゲル関数 |
| RiemannSiegelZ[t] | マン・ジーゲル関数 |
| StieltjesGamma[n] | スティルチェスの定数 |
| Zeta[s] | リーマンのゼータ関数 |
| Zeta[s,a] | 一般化されたリーマンのゼータ関数 |
| HurwitzZeta[s,a] | フルヴィッツのゼータ関数 |
| HurwitzLerchPhi[z,s,a] | フルヴィッツ・レルヒの超越関数 |
リーマンのゼータ関数Zeta[s]は, のとき関係式
のとき関係式  で定義される.整数を引数とするゼータ関数は,各種の総和や積分で使われる.整数を引数とするゼータ関数であれば(一部例外はあるが),厳密な値をWolframシステムで取得することができる.
で定義される.整数を引数とするゼータ関数は,各種の総和や積分で使われる.整数を引数とするゼータ関数であれば(一部例外はあるが),厳密な値をWolframシステムで取得することができる.
スティルチェス(Stieltjes)の定数StieltjesGamma[n]は,オイラーの定数を一般化したもので, を極
を極  の周りで級数展開したときの係数として現れる.
の周りで級数展開したときの係数として現れる.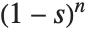 の係数が
の係数が 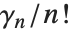 で,オイラーの定数は
で,オイラーの定数は 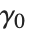 である.
である.
ラマヌジャンの  ディリクレL関数RamanujanTauL[s]は L(s)
ディリクレL関数RamanujanTauL[s]は L(s)
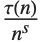 (
(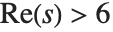 の場合)で定義され,係数RamanujanTau[n]を持つ.リーマンゼータ関数の場合と同様に,関数RamanujanTauZ[t]とRamanujanTauTheta[t]を定義すると便利である.
の場合)で定義され,係数RamanujanTau[n]を持つ.リーマンゼータ関数の場合と同様に,関数RamanujanTauZ[t]とRamanujanTauTheta[t]を定義すると便利である.
多重対数関数PolyLog[n,z]は で与えられる.多重対数関数はジョンキエール(Jonquière)の関数とも呼ばれる.二重対数PolyLog[2,z]は
で与えられる.多重対数関数はジョンキエール(Jonquière)の関数とも呼ばれる.二重対数PolyLog[2,z]は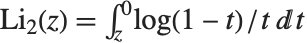 を満足する.
を満足する.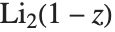 はスペンス(Spence)の積分としても知られている.ニールセンの一般化された多重対数関数あるいは超対数PolyLog[n,p,z]は
はスペンス(Spence)の積分としても知られている.ニールセンの一般化された多重対数関数あるいは超対数PolyLog[n,p,z]は 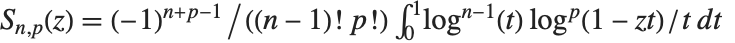 で与えられる.多重対数関数は素粒子論でのファインマン図形の積分および代数的K理論に現れる.
で与えられる.多重対数関数は素粒子論でのファインマン図形の積分および代数的K理論に現れる.
レルヒ(Lerch)の超越関数LerchPhi[z,s,a]は,ゼータ関数および多重対数関数を一般化したもので,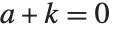 の項を除いた関係式
の項を除いた関係式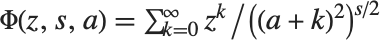 で与えられる.負ベキ乗の和の多くがレルヒの超越関数を使って表せる.例えば,カタランのベータ関数
で与えられる.負ベキ乗の和の多くがレルヒの超越関数を使って表せる.例えば,カタランのベータ関数 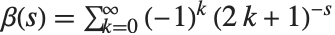 は
は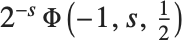 により求めることができる.
により求めることができる.
また,レルヒの超越関数は,整数論に現れるディリクレの L 級数(Dirichlet L‐series )の評価にも使われる.基本 L 級数は 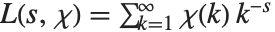 の形を持つ.ここで,「指標」
の形を持つ.ここで,「指標」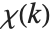 は整数関数で周期
は整数関数で周期 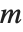 を持つ.この種の L 級数は,
を持つ.この種の L 級数は,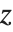 を
を  のベキとおき,レルヒの超越関数の和として書くことができる.
のベキとおき,レルヒの超越関数の和として書くことができる.
指数積分とこれに関連した関数
| CosIntegral[z] | 余弦積分関数 |
| CoshIntegral[z] | 双曲線余弦積分関数 |
| ExpIntegralE[n,z] | 指数積分 En(z) |
| ExpIntegralEi[z] | 指数積分 |
| LogIntegral[z] | 対数積分 |
| SinIntegral[z] | 正弦積分関数 |
| SinhIntegral[z] | 双曲線正弦積分関数 |
対数積分関数LogIntegral[z]は, のとき,
のとき,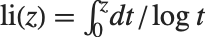 で与えられ,ここで積分の主値が取られる.整数論において
で与えられ,ここで積分の主値が取られる.整数論において は素数の分布解析で中心的な役割を果たす.対数積分関数は,
は素数の分布解析で中心的な役割を果たす.対数積分関数は, とも表記される.整数論の応用の中には,主値を取らず,
とも表記される.整数論の応用の中には,主値を取らず,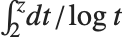 と定義されるものもある.これは,Wolframシステムで定義される
と定義されるものもある.これは,Wolframシステムで定義される とは定数
とは定数 の分だけ違う.
の分だけ違う.
正弦と余弦の積分関数SinIntegral[z]とCosIntegral[z]は, と
と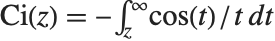 で定義される.双曲線正弦と双曲線余弦の積分関数SinhIntegral[z]とCoshIntegral[z]は
で定義される.双曲線正弦と双曲線余弦の積分関数SinhIntegral[z]とCoshIntegral[z]は ,
,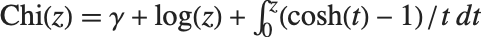 で定義される.
で定義される.
誤差関数とこれに関連した関数
| Erf[z] | 誤差関数 |
| Erf[z0,z1] | 一般化された誤差関数 |
| Erfc[z] | 相補誤差関数 |
| Erfi[z] | 虚部誤差関数 |
| FresnelC[z] | フレネルのC積分 C(z) |
| FresnelS[z] | フレネルのS積分 |
| InverseErf[s] | 逆誤差関数 |
| InverseErfc[s] | 逆相補誤差関数 |
誤差関数Erf[z]は,ガウス分布(正規分布)の密度関数を積分した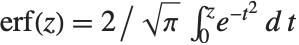 で与えられる.相補誤差関数Erfc[z]は,
で与えられる.相補誤差関数Erfc[z]は,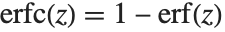 で与えられる.虚部誤差関数Erfi[z]は,
で与えられる.虚部誤差関数Erfi[z]は, で与えられる.一般化された誤差関数Erf[z0,z1]は,積分
で与えられる.一般化された誤差関数Erf[z0,z1]は,積分 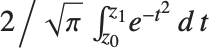 で定義される.誤差関数は統計の計算で中心的な役割を果たしている.
で定義される.誤差関数は統計の計算で中心的な役割を果たしている.
誤差関数に深く関係を持つものに,フレネル(Fresnel)の積分FresnelC[z]およびFresnelS[z]がある.前者は, により,また後者は,
により,また後者は, により定義される.フレネルの積分は回折論の問題で使われる.
により定義される.フレネルの積分は回折論の問題で使われる.
ベッセル関数とこれに関連した関数
| AiryAi[z] および AiryBi[z] | エアリー関数 |
| AiryAiPrime[z] および AiryBiPrime[z] | エアリー関数の導関数 |
| BesselJ[n,z] および BesselY[n,z] | ベッセル関数 |
| BesselI[n,z] および BesselK[n,z] | 変形ベッセル関数 |
| KelvinBer[n,z] および KelvinBei[n,z] | ケルビン関数 |
| KelvinKer[n,z] および KelvinKei[n,z] | ケルビン関数 |
| HankelH1[n,z] および HankelH2[n,z] | ハンケル関数 |
| SphericalBesselJ[n,z] および SphericalBesselY[n,z] | |
球ベッセル関数 | |
| SphericalHankelH1[n,z] および SphericalHankelH2[n,z] | |
球ハンケル関数 | |
| StruveH[n,z] および StruveL[n,z] | シュトルーベ関数 |
球ベッセル関数SphericalBesselJ[n,z]とSphericalBesselY[n,z]は,球ハンケル関数SphericalHankelH1[n,z]およびSphericalHankelH2[n,z]と同様に,球対称の波現象の研究から生じたものである.これらは 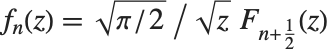 によって,通常の関数と関連している.ハンケル関数の種類によって,関係式の
によって,通常の関数と関連している.ハンケル関数の種類によって,関係式の 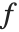 と
と 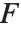 が,それぞれ,
が,それぞれ,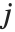 と
と  ,
,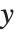 と
と 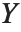 ,または,
,または,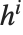 と
と 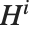 に置き換えられる.整数
に置き換えられる.整数 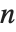 については,特殊ベッセル関数をFunctionExpandを使って初等関数について展開することができる.
については,特殊ベッセル関数をFunctionExpandを使って初等関数について展開することができる.
変形ベッセル関数BesselI[n,z]およびBesselK[n,z]は,微分方程式 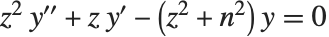 の解である.整数
の解である.整数 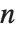 について,
について, で
で 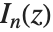 は正則になる一方,
は正則になる一方,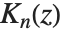 は
は  で対数発散してしまう.
で対数発散してしまう.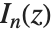 は双曲ベッセル関数としても知 られる.
は双曲ベッセル関数としても知 られる.
特に,電子工学において,ケルビン(Kelvin)関数と呼ばれるKelvinBer[n,z],KelvinBei[n,z],KelvinKer[n,z],KelvinKei[n,z]がよく定義される.これらは通常のベッセル関数と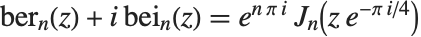 および
および によって関連している.
によって関連している.
エアリー(Airy)関数AiryAi[z]およびAiryBi[z]は,微分方程式 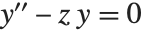 の2つの線形独立な解
の2つの線形独立な解 および
および である.
である. が正で増大するとき
が正で増大するとき は0に収束するが,
は0に収束するが, は限りなく増大する.エアリー関数は,整数の1/3の次数を持つ変形ベッセル関数に関連している.エアリー関数とその導関数AiryAiPrime[z]およびAiryBiPrime[z]は,電磁理論や量子力学の境界値問題によく見られる.
は限りなく増大する.エアリー関数は,整数の1/3の次数を持つ変形ベッセル関数に関連している.エアリー関数とその導関数AiryAiPrime[z]およびAiryBiPrime[z]は,電磁理論や量子力学の境界値問題によく見られる.
シュトルーベ(Struve)関数StruveH[n,z]は整数  に対して
に対して 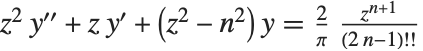 の形式の非斉次ベッセル方程式の解に現れる.この方程式の一般解はシュトルーベ関数
の形式の非斉次ベッセル方程式の解に現れる.この方程式の一般解はシュトルーベ関数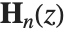 が加えられたベッセル関数の線形結合からなる.変形シュトルーベ関数StruveL[n,z]は通常のシュトルーベ関数から,
が加えられたベッセル関数の線形結合からなる.変形シュトルーベ関数StruveL[n,z]は通常のシュトルーベ関数から, の形式で与えられる.シュトルーベ関数は電磁理論でよく用いられる.
の形式で与えられる.シュトルーベ関数は電磁理論でよく用いられる.
| BesselJZero[n,k] | ベッセル関数 |
| BesselJZero[n,k,x0] | |
| BesselYZero[n,k] | ベッセル関数 |
| BesselYZero[n,k,x0] | |
| AiryAiZero[k] | エアリー関数 |
| AiryAiZero[k,x0] | |
| AiryBiZero[k] | エアリー関数 |
| AiryBiZero[k,x0] |
ルジャンドル関数とこれに関連した関数
| LegendreP[n,z] | 第一種ルジャンドル関数 |
| LegendreP[n,m,z] | 第一種ルジャンドル陪関数 |
| LegendreQ[n,z] | 第二種ルジャンドル関数 |
| LegendreQ[n,m,z] | 第二種ルジャンドル陪関数 |
ルジャンドル関数およびルジャンドル陪関数は,微分方程式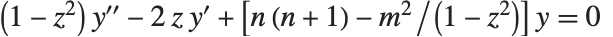 を満たす.第一種ルジャンドル関数LegendreP[n,z]およびLegendreP[n,m,z]は,
を満たす.第一種ルジャンドル関数LegendreP[n,z]およびLegendreP[n,m,z]は,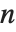 および
および 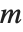 が整数のとき,ルジャンドルの多項式に還元する.第二種ルジャンドル関数LegendreQ[n,z]およびLegendreQ[n,m,z]は,この微分方程式の別な線形独立な解を与える.整数
が整数のとき,ルジャンドルの多項式に還元する.第二種ルジャンドル関数LegendreQ[n,z]およびLegendreQ[n,m,z]は,この微分方程式の別な線形独立な解を与える.整数 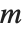 の場合,これらは,
の場合,これらは, において対数的特異点を持つ.
において対数的特異点を持つ.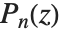 および
および 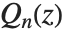 は,
は, のときのこの微分方程式の解である.
のときのこの微分方程式の解である.
| LegendreP[n,m,z] または LegendreP[n,m,1,z] | |
| LegendreP[n,m,2,z] | |
| LegendreP[n,m,3,z] | |
ルジャンドル関数のタイプ(LegendreQも同様なタイプに区分することができる)
タイプ1のルジャンドル関数とタイプ2のルジャンドル関数は,記号形は異なるが,同じ値を持つ.さらに,単位円の外でも定義される.タイプ2の関数は から
から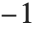 と,
と,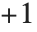 から
から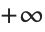 で分岐を持つ.タイプ3のルジャンドル関数は,
で分岐を持つ.タイプ3のルジャンドル関数は, から
から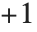 だけで分岐を持つ.タイプ3は
だけで分岐を持つ.タイプ3は 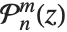 と
と 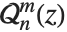 と記述される場合もある.
と記述される場合もある.
同様に,任意の複素数の添数を持つとき,関数GegenbauerC等は,ゲーゲンバウアの関数,チェビシェフの関数,エルミートの関数,ヤコビの関数,そして,ラゲールの関数を与える.ルジャンドルの陪関数と違い,これらの関数において型の区別はされない.
超幾何関数と一般化
| Hypergeometric0F1[a,z] | 超幾何関数 |
| Hypergeometric0F1Regularized[a,z] | 正規化された超幾何関数 |
| Hypergeometric1F1[a,b,z] | クンマーの合流型超幾何関数 |
| Hypergeometric1F1Regularized[a,b,z] | 正規化された合流型超幾何関数 |
| HypergeometricU[a,b,z] | 合流型超幾何関数 |
| WhittakerM[k,m,z] および WhittakerW[k,m,z] | |
ホイッタカー関数 | |
| ParabolicCylinderD[ν,z] | 放物柱関数 |
| CoulombF[l,η,ρ] | 正則クーロン波動関数 |
| CoulombG[l,η,ρ] | 非正則クーロン波動関数 |
ここまでに説明してきた特殊関数の多くは,合流型超幾何関数Hypergeometric1F1[a,b,z]の特殊形と見ることができる.
ホイッタカー(Whittaker)の関数WhittakerM[k,m,z]とWhittakerW[k,m,z] は,ホイッタカーの微分方程式として知られるクンマー微分方程式に解のペアを与える.ホイッタカーの関数 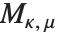 は,
は,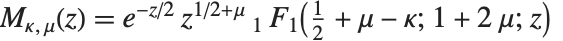 の関係式で
の関係式で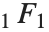 に関連している.第二種のホイッタカーの関数
に関連している.第二種のホイッタカーの関数 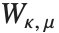 も,
も,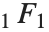 を
を 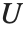 に置き換えると,同じ関係に従う.
に置き換えると,同じ関係に従う.
クーロン(Coulomb)波動関数CoulombF[l,η,ρ]およびCoulombG[l,η,ρ]もまた,合流型超幾何関数の特殊な形のひとつである.クーロン波動関数は,点状核のクーロンポテンシャルにおける放射型シュレーディンガー(Schrödinger)方程式の解を与える.正則なクーロン波動関数は,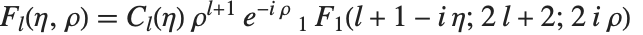 で与えられる.ただし,
で与えられる.ただし,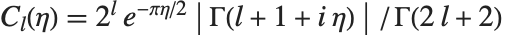 とする.非正則クーロンは導関数
とする.非正則クーロンは導関数 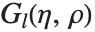 も同様な式で与えられるが,
も同様な式で与えられるが,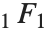 の代りに
の代りに 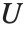 が使われる.
が使われる.
この他に合流型超幾何関数の特殊形としてトロント(Toronto)の関数 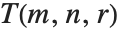 ,ポアソン・シャリェー(Poisson–Charlier)の多項式
,ポアソン・シャリェー(Poisson–Charlier)の多項式  ,カニンガム(Cunningham)の関数
,カニンガム(Cunningham)の関数 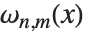 ,そしてベーテマン(Bateman)の関数
,そしてベーテマン(Bateman)の関数 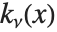 がある.
がある.
| Hypergeometric2F1[a,b,c,z] | 超幾何関数 |
| Hypergeometric2F1Regularized[a,b,c,z] | |
正規化された超幾何関数 | |
| HypergeometricPFQ[{a1,…,ap},{b1,…,bq},z] | |
一般化された超幾何関数 | |
| HypergeometricPFQRegularized[{a1,…,ap},{b1,…,bq},z] | |
正規化され,一般化された超幾何関数 | |
| MeijerG[{{a1,…,an},{an+1,…,ap}},{{b1,…,bm},{bm+1,…,bq}},z] | |
マイヤーのG関数 | |
| AppellF1[a,b1,b2,c,x,y] | 2変数のアッペル超幾何関数 |
マイヤー(Meijer)のG関数MeijerG[{{a1,…,an},{an+1,…,ap}},{{b1,…,bm},{bm+1,…,bq}},z]は線積分表現 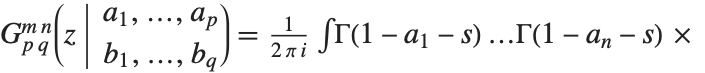
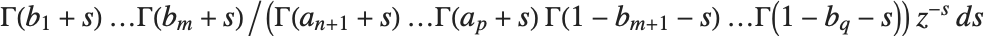 で与えられる.積分路は
で与えられる.積分路は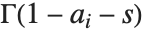 の極と
の極と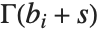 の極の間にあるものとする.マイヤーのG関数MeijerG は非常に一般化された関数であり,これまでの数節で説明してきたほとんどの関数はマイヤーのG関数の特殊形として作ることができる.
の極の間にあるものとする.マイヤーのG関数MeijerG は非常に一般化された関数であり,これまでの数節で説明してきたほとんどの関数はマイヤーのG関数の特殊形として作ることができる.
q 級数関数とこれに関連した関数
| QPochhammer[z,q] | |
| QPochhammer[z,q,n] | |
| QFactorial[z,q] | |
| QBinomial[n,m,q] | |
| QGamma[z,q] | オイラーガンマ関数の |
| QPolyGamma[z,q] | |
| QPolyGamma[n,z,q] | |
| QHypergeometricPFQ[{a1,…,ap},{b1,…,bq},q,z] | |
基本的な超幾何級数 | |
有限の 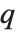 ポッホハンマー記号
ポッホハンマー記号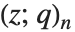 は,積
は,積 で定義される.
で定義される. <1のとき,極限
<1のとき,極限  により
により 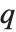 ポッホハンマー記号
ポッホハンマー記号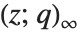 が定義される.
が定義される.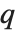 ポッホハンマー記号
ポッホハンマー記号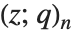 は,極限
は,極限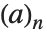
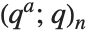 /(1-q)n において回復するポッホハンマー記号
/(1-q)n において回復するポッホハンマー記号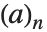 の
の 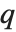 形式である.
形式である.
乗積対数関数
| ProductLog[z] | 乗積対数関数 |
乗積対数関数は,方程式  における
における  についての解を与える.この関数は対数を一般化したものとみなせる.各種の超越方程式の解を表すために使うことができる.明確な分岐の数を数える関数は乗積対数と
についての解を与える.この関数は対数を一般化したものとみなせる.各種の超越方程式の解を表すために使うことができる.明確な分岐の数を数える関数は乗積対数と  の関係にある.
の関係にある.
回転楕円体関数
| SpheroidalS1[n,m,γ,z] および SpheroidalS2[n,m,γ,z] | |
放射状回転楕円体関数 | |
| SpheroidalS1Prime[n,m,γ,z] および SpheroidalS2Prime[n,m,γ,z] | |
放射状回転楕円体関数の z 次導関数 | |
| SpheroidalPS[n,m,γ,z] および SpheroidalQS[n,m,γ,z] | |
回転楕円体角度関数 | |
| SpheroidalPSPrime[n,m,γ,z] および SpheroidalQSPrime[n,m,γ,z] | |
回転楕円体角度関数の z 次導関数 | |
| SpheroidalEigenvalue[n,m,γ] | 次数 n で位数 m の回転楕円体固有値 |
放射状回転楕円体関数のSpheroidalS1[n,m,γ,z]とSpheroidalS2[n,m,γ,z],それに角回転楕円体関数のSpheroidalPS[n,m,γ,z]とSpheroidalQS[n,m,γ,z]は,球状領域における波動方程式の解に見られるものである.どちらの型の関数も,方程式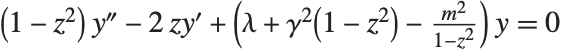 の解となる.この方程式は,
の解となる.この方程式は, が,SpheroidalEigenvalue[n,m,γ]によって与えられる回転楕円体固有値の場合にのみ,正規化可能な解を持つ.回転楕円体関数は,フーリエ(Fourier)変換の有限な相似形の固有関数としても現われる.
が,SpheroidalEigenvalue[n,m,γ]によって与えられる回転楕円体固有値の場合にのみ,正規化可能な解を持つ.回転楕円体関数は,フーリエ(Fourier)変換の有限な相似形の固有関数としても現われる.
SpheroidalS1とSpheroidalS2は,事実上,球状ベッセル(Bessel)関数  と
と  の回転楕円体の相似形であるのに対し,SpheroidalPSとSpheroidalQSはルジャンドル(Legendre)関数
の回転楕円体の相似形であるのに対し,SpheroidalPSとSpheroidalQSはルジャンドル(Legendre)関数 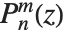 と
と 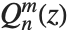 の回転楕円体の相似形である.
の回転楕円体の相似形である. のときは扁長な回転楕円体関数となり,
のときは扁長な回転楕円体関数となり,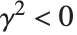 のときは偏球の回転楕円体関数となる.
のときは偏球の回転楕円体関数となる.
楕円積分や楕円関数を使うときは,特殊関数の場合以上に引数の指定には注意を要する.これらの関数の記述や使い方に関しては,相違した規約がしばしば使われる.その多くは,引数の呼び方において違いがあったり,引数と引数の間に入れる区切り記号としてコンマ以外の記号が使われたりする.
■ 振幅 |
■ 引数 |
■ デルタ振幅 |
■ 座標 |
■ 特性 |
■ パラメータ |
■ 補パラメータ |
■ 母数(Modulus) |
■ モジュラ角 |
■ ノーム |
■ 不変数 |
■ 半周期 |
■ 周期の比 |
■ 判別式 |
■ 曲線のパラメータ |
■ 座標 |
| JacobiAmplitude[u,m] | 引数 u とパラメータ m に対応した振幅 ϕ を返す |
| EllipticNomeQ[m] | パラメータ m に対応したノーム q を返す |
| InverseEllipticNomeQ[q] | ノーム q に対応したパラメータ m を返す |
| WeierstrassInvariants[{ω,ω′}] | 半周期{ω,ω′}に対応した不変数{g2,g3}を返す |
| WeierstrassHalfPeriods[{g2,g3}] | 不変数{g2,g3}に対応した半周期{ω,ω′}を返す |
楕円積分
| EllipticK[m] | 第一種完全楕円積分 |
| EllipticF[ϕ,m] | 第一種楕円積分 |
| EllipticE[m] | 第二種完全楕円積分 E(m) |
| EllipticE[ϕ,m] | 第二種楕円積分 E(ϕm) |
| EllipticPi[n,m] | 第三種完全楕円積分 |
| EllipticPi[n,ϕ,m] | 第三種楕円積分 |
| JacobiZeta[ϕ,m] | ヤコビのゼータ関数 |
第一種完全楕円積分EllipticK[m] は,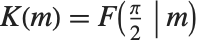 で与えられる.ここで,
で与えられる.ここで, は第一種完全楕円積分を表し,
は第一種完全楕円積分を表し,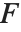 は不完全楕円積分を表すことに注目されたい.実際の用途では,
は不完全楕円積分を表すことに注目されたい.実際の用途では,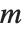 が省略れ,
が省略れ, は単に
は単に  と記述されることがよくある.補第一種完全楕円積分
と記述されることがよくある.補第一種完全楕円積分 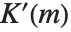 は,
は, で与えられる.この積分はしばしば
で与えられる.この積分はしばしば  とも表記される.
とも表記される. と
と 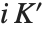 は,対応するヤコビの楕円積分(「楕円関数」を参照)の「実部」と「虚部」の各々からなる四分の一周期を与える.
は,対応するヤコビの楕円積分(「楕円関数」を参照)の「実部」と「虚部」の各々からなる四分の一周期を与える.
楕円関数
| JacobiAmplitude[u,m] | 振幅関数 |
| JacobiSN[u,m] , JacobiCN[u,m]等 | ヤコビの楕円関数 |
| InverseJacobiSN[v,m] , InverseJacobiCN[v,m]等 | 逆ヤコビの楕円関数 |
| EllipticTheta[a,u,q] | 楕円シータ関数 |
| EllipticThetaPrime[a,u,q] | 楕円シータ導関数 |
| SiegelTheta[τ,s] | シーゲルのシータ関数 |
| SiegelTheta[v,τ,s] | シーゲルのシータ関数 |
| WeierstrassP[u,{g2,g3}] | ワイエルシュトラスの楕円関数 |
| WeierstrassPPrime[u,{g2,g3}] | ワイエルシュトラスの楕円導関数 |
| InverseWeierstrassP[p,{g2,g3}] | 逆ワイエルシュトラスの楕円関数 |
| WeierstrassSigma[u,{g2,g3}] | ワイエルシュトラスのシグマ関数 |
| WeierstrassZeta[u,{g2,g3}] | ワイエルシュトラスのゼータ関数 |
ヤコビの楕円関数JacobiPQ[u,m] は全部で12種類存在する.それらは,P とQ をS,C,D,Nから組み合せることで作れる.それぞれのヤコビの楕円関数JacobiPQ[u,m] は, を満足する.ただし,この式では
を満足する.ただし,この式では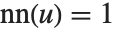 とする.
とする.
三角関数の間にはさまざまな関係式があるが,それに似た関係がヤコビの楕円関数の間にも数多くある.ヤコビの楕円関数は,極限を取ったとき,三角関数に還元する.このため, ,
, ,
, ,
, ,
,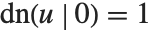 ,
, というような関係が成り立つ.
というような関係が成り立つ.
楕円関数の重要な特性のひとつとして,引数の複素数値について二重の周期性を持つことが挙げられる.通常の三角関数は単一な周期性を持つ.つまり,任意の整数 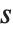 について
について  の周期性を持つ.これに対して,楕円関数は二重周期性を持つ.つまり,
の周期性を持つ.これに対して,楕円関数は二重周期性を持つ.つまり, の周期性が
の周期性が 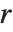 と
と 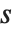 の任意の整数の対について成り立つ.
の任意の整数の対について成り立つ.
Wolfram言語には,逆ヤコビの楕円関数であるInverseJacobiSN[v,m]やInverseJacobiCN[v,m]等も組み込まれている.例えば,逆関数の1つ,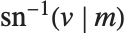 は,
は, が成り立つための
が成り立つための 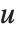 の値を与える.逆ヤコビの楕円関数は楕円積分に関連している.
の値を与える.逆ヤコビの楕円関数は楕円積分に関連している.
4種類の楕円シータ関数 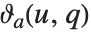 は,a を1,2,3または4としてEllipticTheta[a,u,q] から作ることができる.これらの関数は,
は,a を1,2,3または4としてEllipticTheta[a,u,q] から作ることができる.これらの関数は,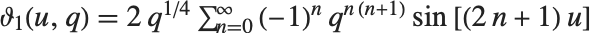 ,
,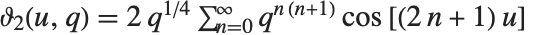 ,
, ,
,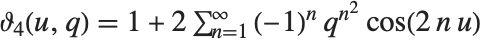 で定義される.シータ関数はパラメータ
で定義される.シータ関数はパラメータ 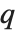 を明示しないで
を明示しないで  と書かれることもある.シータ関数は,
と書かれることもある.シータ関数は,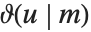 と書かれることもあるが,その場合に
と書かれることもあるが,その場合に 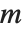 と
と 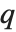 は
は 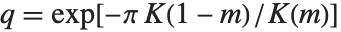 という式で関係付けられている.また,
という式で関係付けられている.また,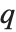 は
は 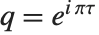 で与えられる
で与えられる  に置き換えられることもある.これらすべてのシータ関数は拡散方程式
に置き換えられることもある.これらすべてのシータ関数は拡散方程式  を満たす.
を満たす.
次元 p,ベクトル s のリーマンの正方モジュラ行列  を持つシーゲルのシータ関数SiegelTheta[τ,s]は,複素次元 p までの楕円シータ関数を生成する.これは
を持つシーゲルのシータ関数SiegelTheta[τ,s]は,複素次元 p までの楕円シータ関数を生成する.これは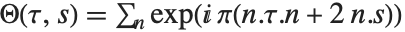 で定義され,n はすべての p 次元整数ベクトル上を動く.特性関数SiegelTheta[ν,τ,s] を持つシーゲルのシータ関数は,
で定義され,n はすべての p 次元整数ベクトル上を動く.特性関数SiegelTheta[ν,τ,s] を持つシーゲルのシータ関数は, で定義され,特性 ν は1対の p 次元ベクトル{α,β} を表す.
で定義され,特性 ν は1対の p 次元ベクトル{α,β} を表す.
ワイエルシュトラス(Weierstrass)の楕円関数WeierstrassP[u,{g2,g3}] は,楕円積分の逆関数と見ることができる.ワイエルシュトラスの関数 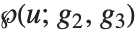 は,
は,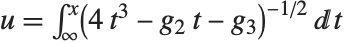 を満たす
を満たす 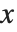 の値を与える.関数WeierstrassPPrime[u,{g2,g3}]は,
の値を与える.関数WeierstrassPPrime[u,{g2,g3}]は, で与えられる.
で与えられる.
逆ワイエルシュトラスの楕円関数InverseWeierstrassP[{p,q},{g2,g3}]は,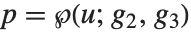 および
および 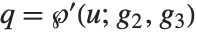 となる
となる 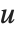 の一意的な値を返す.
の一意的な値を返す.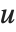 にそのような値が存在するには,
にそのような値が存在するには,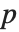 と
と 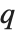 は
は  の関係式を満たす必要がある.
の関係式を満たす必要がある.
ワイエルシュトラスのゼータ関数WeierstrassZeta[u,{g2,g3}] とワイエルシュトラスのシグマ関数WeierstrassSigma[u,{g2,g3}]は,ワイエルシュトラスの楕円関数に各々, と
と 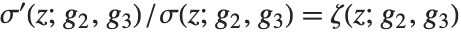 の関係式で関連している.
の関係式で関連している.
楕円モジュラ関数
| DedekindEta[τ] | デデキントのイータ関数 |
| KleinInvariantJ[τ] | クラインの不変モジュラ関数 |
| ModularLambda[τ] | モジュラ・ラムダ関数 |
一般化された楕円積分と楕円関数
| ArithmeticGeometricMean[a,b] | |
| EllipticExp[u,{a,b}] | 楕円曲線 |
| EllipticLog[{x,y},{a,b}] | 楕円曲線 |
関数EllipticLog[{x,y},{a,b}]は,積分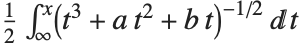 の値として定義される.ただし,平方根の符号は
の値として定義される.ただし,平方根の符号は 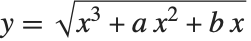 とする
とする 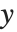 を与えることで指定する.
を与えることで指定する.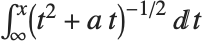 の形の積分は,常用対数(および,逆三角関数)を用いて表せる.平方根でくくられた多項式を三次にして,これを一般化したのがEllipticLogと考えるとよい.
の形の積分は,常用対数(および,逆三角関数)を用いて表せる.平方根でくくられた多項式を三次にして,これを一般化したのがEllipticLogと考えるとよい.
EllipticExp[u,{a,b}]はEllipticLogの逆関数である.この関数はEllipticLogに引数としてある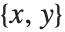 のリストを返す.EllipticExpは楕円関数で,複素
のリストを返す.EllipticExpは楕円関数で,複素  平面上で二重周期を持つ.
平面上で二重周期を持つ.
ArithmeticGeometricMean[a,b]は,2個の数 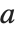 と
と 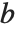 の算術幾何平均(AGM)を返す.この量は,楕円積分や他の関数を計算する数値アルゴリズムにおいて中心的な役割を果たす.
の算術幾何平均(AGM)を返す.この量は,楕円積分や他の関数を計算する数値アルゴリズムにおいて中心的な役割を果たす. と
と  を初期値として,必要な精度の下で
を初期値として,必要な精度の下で  となるまで変換
となるまで変換 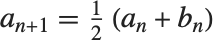 ,
,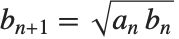 を繰り返すことで,AGMが求まる.
を繰り返すことで,AGMが求まる.
| MathieuC[a,q,z] | 特性値 a とパラメータ q を持つマシューの偶関数 |
| MathieuS[b,q,z] | 特性値 b とパラメータ q を持つマシューの奇関数 |
| MathieuCPrime[a,q,z] および MathieuSPrime[b,q,z] | マシューの関数の z による導関数 |
| MathieuCharacteristicA[r,q] | 特性指数 r とパラメータ q を持つマシューの偶関数のための特性値 ar |
| MathieuCharacteristicB[r,q] | 特性指数 r とパラメータ q を持つマシューの偶関数のための特性値 br |
| MathieuCharacteristicExponent[a,q] | 特性値 a とパラメータ q を持つマシューの奇関数のための特性指数 r |
マシュー(Mathieu)の関数MathieuC[a,q,z]とMathieuS[a,q,z]は,方程式  の解である.この方程式は楕円形や周期性ポテンシャルにかかわった多くの物理問題で見られる.関数MathieuCは
の解である.この方程式は楕円形や周期性ポテンシャルにかかわった多くの物理問題で見られる.関数MathieuCは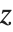 について偶となるよう定義され,MathieuSは奇となるよう定義される.
について偶となるよう定義され,MathieuSは奇となるよう定義される.
フロケ(Floquet)の定理によると,任意のマシューの関数を 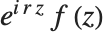 の形で書くことができる.ここで,
の形で書くことができる.ここで, は周期
は周期 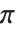 を持ち,
を持ち,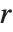 はマシューの特性指数MathieuCharacteristicExponent[a,q]である.したがって,特性指数
はマシューの特性指数MathieuCharacteristicExponent[a,q]である.したがって,特性指数 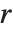 が整数,または,有理数を取るとき,マシューの関数は周期性を持つ.ただし,一般に,
が整数,または,有理数を取るとき,マシューの関数は周期性を持つ.ただし,一般に,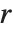 が実整数でないとき
が実整数でないとき 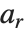 と
と 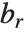 は等しい.
は等しい.
自動評価 | 特定の引数に対し厳密な結果を返す |
| N[expr,n] | 任意精度で数値近似する |
| D[expr,x] | 厳密な導関数を返す |
| N[D[expr,x]] | 導関数を数値近似する |
| Series[expr,{x,x0,n}] | 級数展開 |
| Integrate[expr,x] | 厳密に積分する |
| NIntegrate[expr,x] | 積分を数値近似する |
| FindRoot[expr==0,{x,x0}] | 根を数値近似する |
ほとんどの引数では特殊関数を厳密に簡約することは不可能である.そのようなときでも,Wolframシステムの数値近似機能を使い必要な精度で特殊関数の近似値を得ることはできる.Wolframシステムに組み込まれているアルゴリズムは,特殊関数を定義するパラメータが基本的にどんな値を取ろうが対応できるようになっている.パラメータが実数であっても,複素数であっても対応可能である.
ほとんどの特殊関数では,その導関数を初等関数や別の特殊関数で表すことが可能である.そうすることが不可能なときでも,Nを適用することで数値近似的な導関数の値を求めることは可能である.
それでも,Nを使えば近似値を得ることができる:
Wolframシステムには特殊関数に関する知識が大量に集約されている.基本的には過去に導出された,特殊関数に関するすべての研究結果が入っている.Wolframシステムで特殊関数を使うたびに,ユーザはこの知識にアクセスしていることになる.
| FullSimplify[expr] | 各種変換規則を使い式 expr を簡約する |
| FunctionExpand[expr] | 特殊関数の展開形を求める |
ここでは,PolyGammaを使わなくても最終式が求まる: